下面的解析是來自洛谷的題解。 

前言

• SPFASPFA演算法由於它上限 O(NM) = O(VE)O(NM)=O(VE)的時間複雜度,被卡掉的機率很大.在演算法競賽中,我們需要一個更穩定的演算法:dijkstradijkstra.

什麼是dijkstradijkstra?

• dijkstradijkstra是一種單源最短路徑演算法,時間複雜度上限為O(n^2)O(n2)(樸素),在實際應用中較為穩定;;加上堆優化之後更是具有O((n+m)\log_{2}n)O((n+m)log2​n)的時間複雜度,在稠密圖中有不俗的表現.

dijkstradijkstra的原理/流程?

• dijkstradijkstra本質上的思想是貪心,它只適用於不含負權邊的圖.
• 我們把點分成兩類,一類是已經確定最短路徑的點,稱為"白點",另一類是未確定最短路徑的點,稱為"藍點"
• dijkstradijkstra的流程如下::
• 1.1. 初始化dis[start] = 0,dis[start]=0,其餘節點的disdis值為無窮大.
• 2.2. 找一個disdis值最小的藍點x,x,把節點xx變成白點.
• 3.3. 遍歷xx的所有出邊(x,y,z),(x,y,z),若dis[y] > dis[x] + z,dis[y]>dis[x]+z,則令dis[y] = dis[x] + zdis[y]=dis[x]+z
• 4.4. 重複2,32,3兩步,直到所有點都成為白點..
• 時間複雜度為O(n^2)O(n2)

dijkstradijkstra為什麼是正確的

• 當所有邊長都是非負數的時候,全域性最小值不可能再被其他節點更新.所以在第22步中找出的藍點xx必然滿足:dis[x]:dis[x]已經是起點到xx的最短路徑..我們不斷選擇全域性最小值進行標記和拓展,最終可以得到起點到每個節點的最短路徑的長度

圖解

• (令start = 1start=1)
• 開始時我們把dis[start]dis[start]初始化為00,其餘點初始化為infinf 
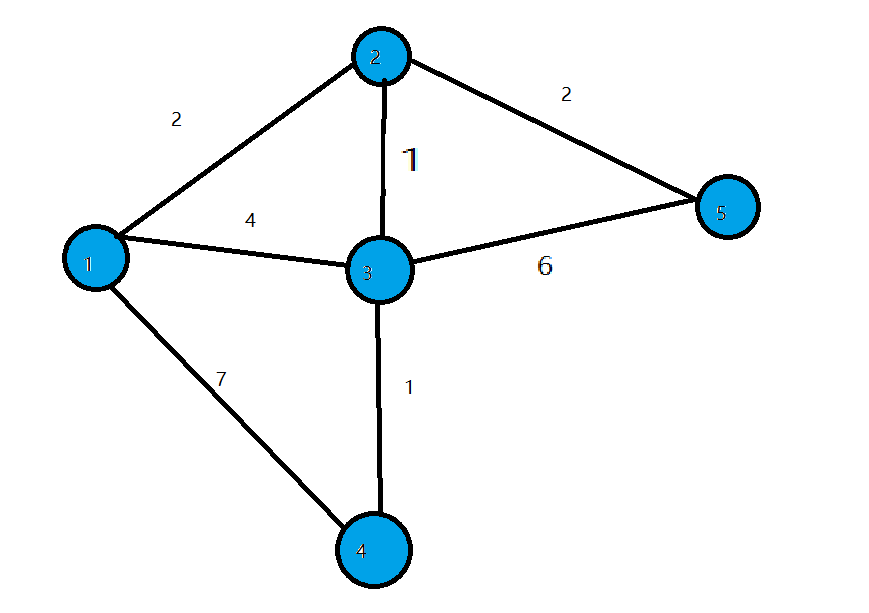
• 第一輪迴圈找到disdis值最小的點11,將11變成白點,對所有與11相連的藍點的disdis值進行修改,使得dis[2]=2,dis[3]=4,dis[4]=7dis[2]=2,dis[3]=4,dis[4]=7 
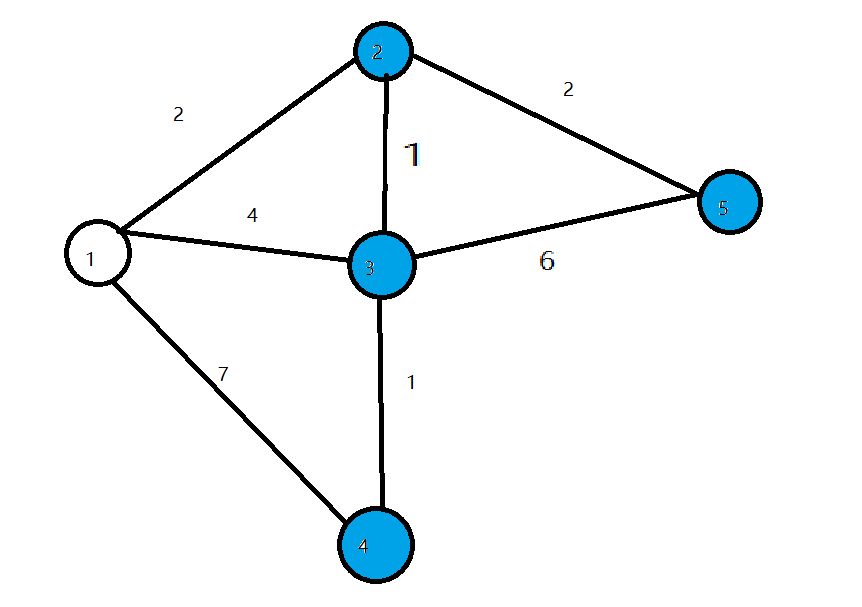
• 第二輪迴圈找到disdis值最小的點22,將22變成白點,對所有與22相連的藍點的disdis值進行修改,使得dis[3]=3,dis[5]=4dis[3]=3,dis[5]=4 
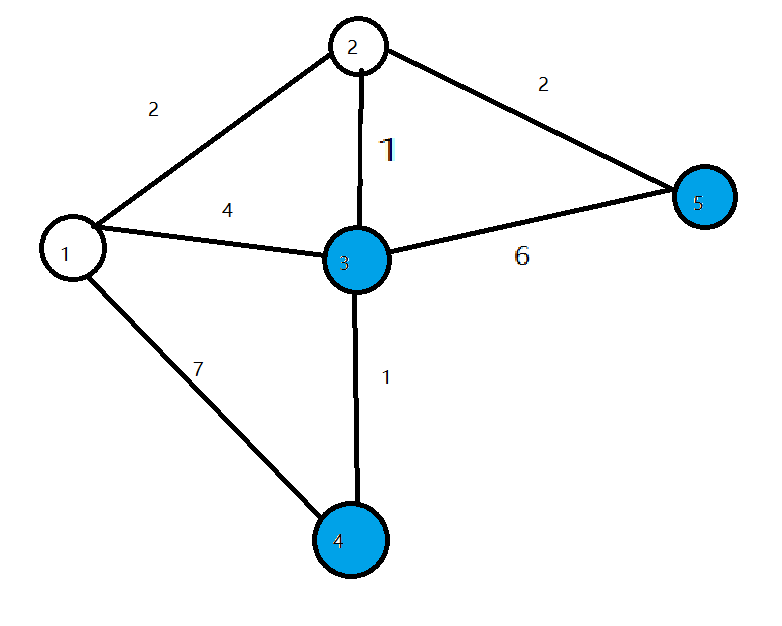
• 第三輪迴圈找到disdis值最小的點33,將33變成白點,對所有與22相連的藍點的disdis值進行修改,使得dis[4]=4dis[4]=4 
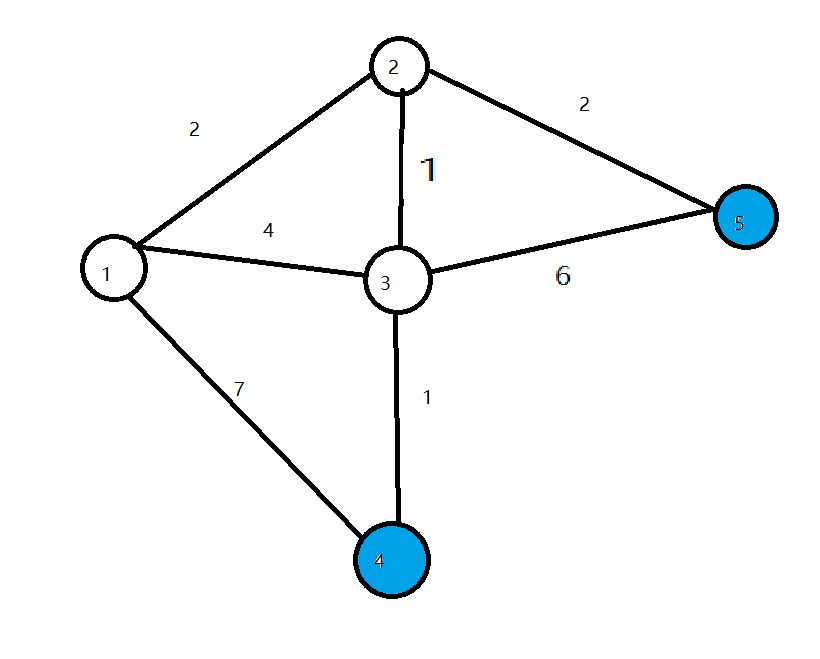
• 接下來兩輪迴圈分別將4,54,5設為白點,演算法結束,求出所有點的最短路徑
• 時間複雜度O(n^2)O(n2)

為什麼dijkstradijkstra不能處理有負權邊的情況?

• 我們來看下面這張圖 
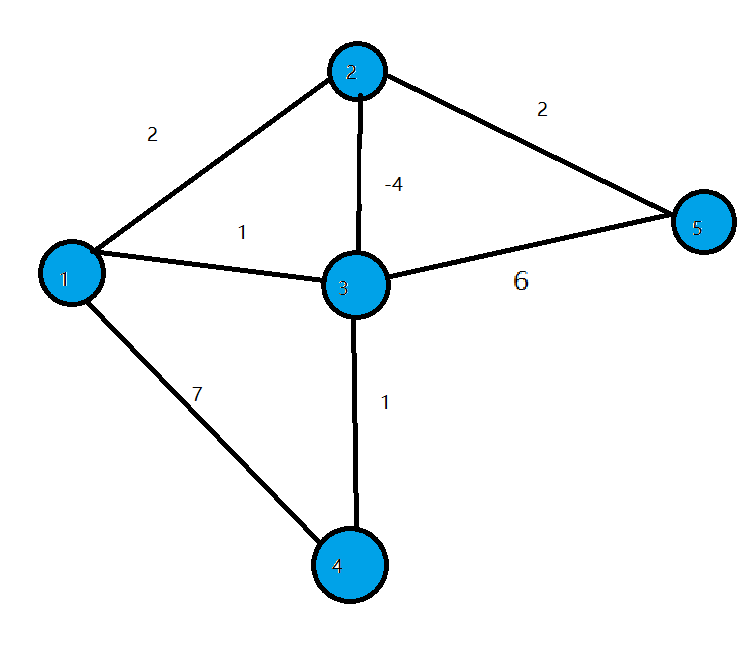
• 22到33的邊權為-4−4,顯然從11到33的最短路徑為-2−2 (1->2->3).(1−>2−>3).但在迴圈開始時程式會找到當前disdis值最小的點33,並標記它為白點.
• 這時的dis[3]=1,dis[3]=1,然而11並不是起點到33的最短路徑.因為33已經被標為白點,所以dis[3]dis[3]不會再被修改了.我們在邊權存在負數的情況下得到了錯誤的答案.

dijkstradijkstra的堆優化?

• 觀察dijkstradijkstra的流程,發現步驟22可以優化

• 怎麼優化呢?

• 我會zkw線段樹!我會斐波那契堆!

• 我會堆!

• 我們可以用堆對disdis陣列進行維護,用O(\log_{2}n)O(log2​n)的時間取出堆頂元素並刪除,用O(\log_{2}n)O(log2​n)遍歷每條邊,總複雜度O((n+m)\log_{2}n)O((n+m)log2​n)

head陣列和edge[i]裡面的next元素聯合用的真是無敵了，可以通過一個迴圈直接訪問到任意一個點周圍的所有點。

//我覺的理解這段程式碼最重要的就是理解head陣列和e[]結構體數組裡面next元素的結合用法。
//比如我輸入1——2 1——3 1——4 1——5
//add_edge裡面的處理之後,e[1],e[2],e[3],e[4]裡面儲存的是這四條邊的資訊
//最終head[1]=4;表示的是1（最後輸入）最後直接相連的邊的序號是4
//然後訪問e[4],e[4].next會是3，表示比當前邊1——4更早相連的邊的資訊儲存在序號為3的結構體陣列e中
#include <bits/stdc++.h>
using namespace std;
int N,M,S;
#define inf 0x3f3f3f3f
const int maxn=100005;
int dis[maxn],head[maxn];
int cnt;
int vis[maxn];
struct edge{
	int to,next,dis;
}e[maxn*5];
struct node{
	int dis;
	int pos;
	bool operator<(const node x)const{
		return this->dis>x.dis;
	} 
};

priority_queue<node> q;

void add_edge(int u,int v,int dis)
{
	cnt++;
	e[cnt].to=v;
	e[cnt].dis=dis;
	e[cnt].next=head[u];//這個串聯用的真是巧妙
	head[u]=cnt;//這個串聯用的真是巧妙
}

void dijkstra()
{
	dis[S]=0;
	node temp;
//	temp.dis=0,temp.pos=S;
//	q.push(temp);
	q.push((node){0,S});
	while(!q.empty())
	{
		temp=q.top();
		q.pop();
		int x=temp.pos;
		if(vis[x]) continue;
		vis[x]=1;
		for(int i=head[x];i;i=e[i].next) 
		{
			int y=e[i].to;
			if(dis[y]>dis[x]+e[i].dis){
				dis[y]=dis[x]+e[i].dis;
				temp.dis=dis[y],temp.pos=y;
				if(!vis[y]) q.push(temp);
			}
		}
	}
}

int main()
{
	cin>>N>>M>>S;
	int i,j,k,u,v,len;
	for(i=0;i<M;i++){
		scanf("%d%d%d",&u,&v,&len);
		add_edge(u,v,len);
	}	
	for(i=0;i<=N;i++)
		dis[i]=inf;
	dijkstra();
	for(i=1;i<=N;i++){
		printf("%d",dis[i]);
		if(i!=N) printf(" ");
		else printf("\n");
	}
	return 0;
}