機器學習技法 Lecture6: Support Vector Regression
機器學習技法 Lecture6: Support Vector Regression
1. Kernel Ridge Regression
先回憶一下之前講的representer理論,也就是L2正則化的線性分類模型的最佳解都能用樣本點來線性表示。也就是說都能夠使用核方法:

講解正則化的時候講過,帶正則項的線性迴歸問題有解析解,也叫作Ridge Regression。那麼使用了核方法的情況如何呢?

鞍迴歸的目標函式如下所示,且最優解能夠使用樣本點表示:

將最優解的表示代入目標函式且替換為核方法,可以得到一個新的關於係數 的目標函式:

直接求梯度,令梯度為0,同樣能夠得到鞍迴歸的解析解:

這個解法需要 的複雜度。不過現在利用了核方法就能夠輕鬆地解非線性的鞍迴歸問題。
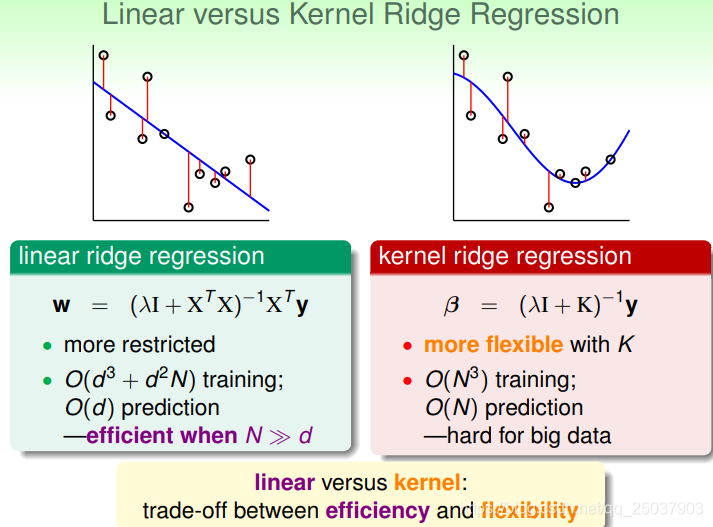
對比線性的鞍迴歸問題與利用了核方法的鞍迴歸解法,可以發現使用了核方法給問題的解決帶來了靈活性,但同時也需要更復雜的計算。
2. Support Vector Regression Primal
使用了核方法的鞍迴歸問題也叫作最小平方SVM,簡稱LSSVM。對比普通的軟間隔SVM與LSSVM的結果我們可以發現使用了LSSVM得到的結果雖然與SVM的結果很相近,但是LSSVM裡每個點都會影響結果,大部分系數
都是非0的,也就會導致更慢的計算。

如果我們希望能夠得到一種使用核方法的迴歸,但是係數
也類似軟間隔SVM裡比較稀疏。
可以考慮一個叫做Tube Regression的設定,那就是當樣本點距離分隔面某個距離之內時,目標函式不加懲罰,超出這個距離的,乘法部分減去這個距離。
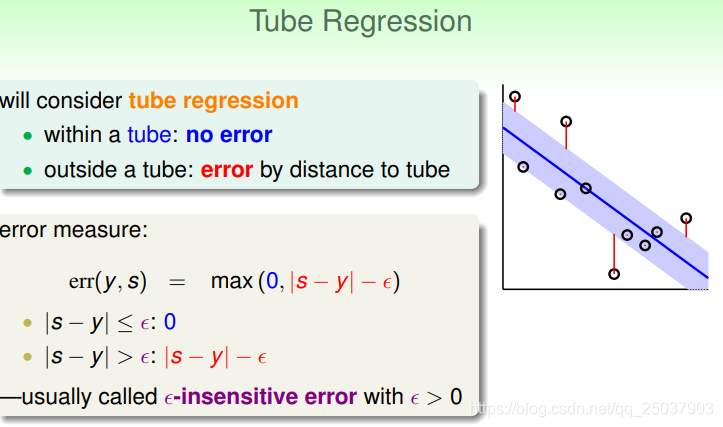
下一步就是希望在這個設定下加入L2正則化,同時得到比較係數的係數
。可以先看一下這個問題的error與 普通線性迴歸的error的區別:

可以看到距離比較近的時候兩個error很接近,但是錯誤較大時Tube Regression的error增長較慢,可能更不易收到outlier的影響。
寫出加入L2正則化的目標函式:

與標準的SVM問題對比可以發現,差距主要是無法二次規劃可解且不能帶來稀疏的係數結果。因此我們需要改造目標函式使其接近標準SVM問題:

因為目標函式裡有個絕對值項,因此需要兩個鬆弛變數作為上下界,這樣就能使目標函式接近標準SVM的形式:

最終就得到了一個同樣二次規劃可解的問題,叫做SVR的原始問題:

同樣的,為了移除問題對於變換後的維度
的影響,需要利用對偶問題來求解。
3. Support Vector Regression Dual
同樣使用拉格朗日乘子法將限制條件代入目標函式求解,然後利用其對偶問題在滿足KKT條件下的解來作為原問題的解:

整個過程和之前SVM對偶的問題裡一樣。我們可以對比一下得到的對偶問題的形式:

可以看到它們的形式很接近,也能夠用同樣的QP來解。
和軟間隔SVM得到的結果相似,SVR得到的結果也有一些對鬆弛變數的限制條件,而這些限制條件帶來了結果的稀疏性:

4. Summary of Kernel Models
在這裡做一個到目前為止模型的總結。首先我們講了幾個線性模型,PLA、線性迴歸、邏輯迴歸,線性SVM和線性SVR。
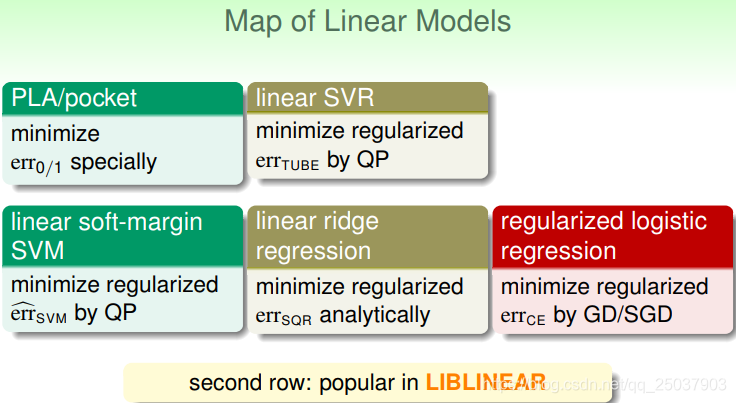
第二行的三種結果比較常用。第一行兩種不常用的原因是它們需要比較大的計算量。
線上性模型的基礎上使用核方法,又得到了幾種非線性的模型。第四行的三種平時比較常用,第三行不常用因為它們的結果沒有稀疏性:
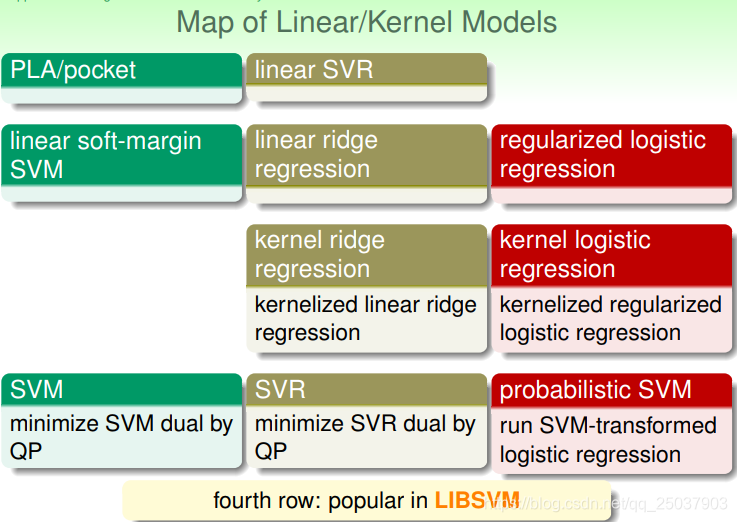
一般來說使用的核方法有多項式、高斯形式等,也可以自己定義一個核方法,但是需要滿足核方法的Mercer‘s condition(也就是寫為矩陣半正定,而且有對稱性)。
但是也要記住,使用核方法能帶來更多靈活性和更強的模型同時,有可能也會帶來更多的計算量,以及更容易過擬合等問題。
