機器學習技法 Lecture2: Dual Support Vector Machine

• Motivation of Dual SVM
• Lagrange Dual SVM
• Solving Dual SVM
• Messages behind Dual SVM

Motivation of Dual SVM

首先回顧上節課講的SVM，如果把其中的 $x_n$

x_{n} 加上一個對映變換，就會得到以下形式的問題：

這樣做能夠得到一個帶有非線性分隔面的結果。但是這樣的方式會依賴於對映之後的假設空間的VC維，太大的話很難解。因此就想要得到一種不依賴於新的VC維的解法。

為了得到這個等價的SVM需要進行很多的數學推導，有時候也會直接用一些數學結論。這個等價的SVM是基於原始SVM的對偶問題的。

這裡需要用到一個很關鍵的方法就是拉格朗日乘子法。這個方法在之前講到的正則化裡面也用到過。不過那裡用到的時候是把係數 $\lambda$

\lambda 當做是一個已知的常數來解，因此用起來相對簡單。但是在SVM的拉格朗日乘子法問題裡是把 $\lambda$當做是一個變數來使用。不過在這裡不用 $\lambda$

來表示而是使用了 $\alpha_{n}$。又因為SVM裡面有 $N$個限制條件，因此也會有 $N$個係數。於是我們得到新的SVM的形式為：

這樣就把一個帶約束問題轉為一個無約束問題。新的問題裡每一個係數 $\alpha_{n}$都大於0。而新的函式目標同樣是最小化一個式子的結果，但是這個式子的結果與 $\alpha$的取值有關，因此最小化的是對於係數 $\alpha$最大化之後的結果。

而對於新的目標函式來說，有 $N$個項是對應原來的約束條件。當這些項遇到不滿足條件的 $(b,w)$，項就是一個正值。而對 $\alpha$取max的結果就會是無窮大，因此不會取到這個對應的結果作為外層min的結果。於是最終的結果中，約束條件還是隱式被滿足的。

Lagrange Dual SVM

首先如果把係數 $\alpha$固定，那麼這個結果肯定是小於等於原來的目標函式的結果。

而對於這個固定了 $\alpha$的式子來說也有一個對於 $\alpha$的最大值，不過這個值還是會小於等於原來式子的結果。

不等式右邊的問題就是這個問題的拉格朗日對偶問題。

在二次規劃中，這種不等式形式的對偶問題叫做弱對偶形式。但是若對偶的二次規劃問題，如果滿足了一些條件，等式就能夠成立。這些條件叫做constraint qualification。而這個SVM的拉格朗日對偶能夠滿足這些條件，因此存在一組解同時是不等式兩邊都得到最優解。

下面對這個對偶問題進行第一步的化簡。首先看括號裡min的部分。對於這個問題求最小，由於是個凸問題，所以最優解肯定是在梯度為0的位置。對b求導令導數為0。之後發現帶著這個導數為0的約束可以將式子中的一項去掉而不影響結果。

第二步對 $w$進行求導，令導數為0同樣得到一個約束。這個約束也可以化簡目標函式：

而對於對偶問題的最優解，如果滿足KKT條件，那麼這個解也是原問題的最優解。其中KKT條件有四個部分：原問題可行性（primal feasible）、對偶問題可行性（dual feasibl）、對偶內部最優（dual-inner optimal）和原問題內部最優（primal-inner optimal）。

Solving Dual SVM

由上面的推導得到了SVM對偶問題的化簡形式：

由於需要滿足KKT條件，又多出了限制條件。不過這個問題最終是得到了一個像最初期望的那樣，有N個變數和N+1個限制條件的問題，去掉了對於對映之後的維度的依賴。這個問題還是用二次規劃來解決。

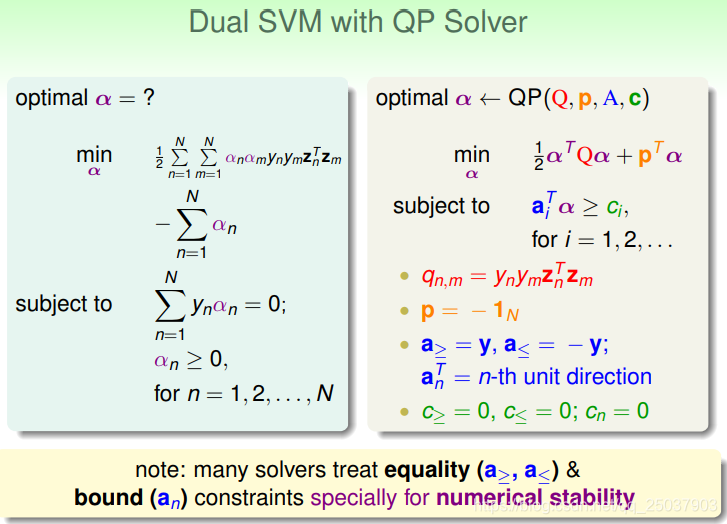
需要將等式約束寫為兩個不等式約束來滿足二次規劃的標準形式。

但是對於這樣的二次規劃依然存在一些問題。因為q一般是非0，因此Q矩陣是個密集的矩陣。如果N比較大，就會導致需要很大的儲存空間。因此對於比較大的N有時候需要比較特殊的解二次規劃的方法。

對於最終的結果，需要滿足KKT條件。因此我們看到這四個不同的條件對應了不同的等式或不等式。而當我們得到了最優的 $\alpha$時，能夠很輕鬆的根據等式得到最終的係數 $w$。

但是對於係數 $b$來說，。有兩個限制條件。一個是primal feasible裡限制的不等式 $y_{n}(w^{T}z_{n}+b)\geq 1$或者從另外一個primal-inner的等式限制中得到。 $\alpha_{n}(1-y_{n}(w^{T}z_{n}+b))=0$。而對於這個等式需要滿足的是如果 $\alpha_{n}\geq 0$，那麼對應的係數 $b=y_{n}-w^{T}z_{n}$。而滿足這個條件的點都在距離分隔面最近的邊界上，也就是support vector。只有滿足 $\alpha_{n}\geq 0$的邊界上的點才叫做support vector。

Messages behind Dual SVM

因此對於最終的結果來說，只有最靠近分隔面的點才會影響結果。而且對於 $\alpha_{n} \geq 0$的點叫做support vectors。也就是說在邊界上的點包含了support vector的集合（因為邊界上的點不一定滿足 $\alpha_{n} \geq 0$，但不在邊界上的點肯定不滿足）。

因此對於結果來說，只需要計算support vectors的貢獻即可：

於是SVM就是一個通過使用對偶最優的結果得到邊界上的support vector最終得出一個有寬度的分隔面的演算法。

其中w的結果是通過資料的計算來得到，這和PLA演算法裡的係數演算法很像。對於這種結果我們叫做w ‘represented’ by data。而SVM裡的w只通過支援向量來表示。

最後我們得到了兩種形式的svm演算法，一個是原始的SVM問題，一個是用對偶問題解的對偶型是。原始問題依賴於對映後的平面的維度，而對偶問題在N比較小時只依賴於變數數N。原始問題的物理意義是找到通過特定縮放限制的(w,b)，而對偶問題的物理意義是找到support vectors和他們對應的 $\alpha_{n}$。最終都得到一個線性分類器。

但實際上我們的工作並沒有做完。因為我們的目標是拜託對於對映後的維度 $\widehat{d}$的依賴，但實際上在其中的內積運算時還是依賴於這個值。因此還有下一步的工作要做。