機器學習技法 Lecture4: Soft-Margin Support Vector Machine

• Motivation and Primal Problem
• Dual Problem
• Messages behind Soft-Margin SVM
• Model Selection

Motivation and Primal Problem

Hard-Margin SVM有個缺點那就是它依然會過擬合。原因一部分是對映函式 $\mathrm{\Phi }$

\Phi 造成的，而另一部分原因是它對於線性可分的要求。

為了緩解過擬合的情況，可以放鬆對於線性可分的要求。也就是可以讓部分樣本點分錯。對於這種情況之前講過一個演算法很相似，那就是pocket PLA演算法。pocket演算法裡對於不可分的點的做法是最小化分錯的數量。可以把這種做法與Hard-Margin SVM結合一下，把原來的最小化目標加上一個分錯數量的部分：

對應的限制條件也要改。對於分對的要大於1，分錯的就不管了。不過這個方式得到的這種演算法有個很大的問題，那就是判斷分對分錯的函式是個非線性的函式，不再是二次規劃可解的問題。而且這種只判斷分對分錯的方式也無法區分出錯誤的點錯誤的程度。

於是可以使用一種新的目標函式，能夠方便得看出分錯的程度，而且能夠使最終的目標函式是二次規劃可解的。

使用了一個新的變數 $\xi$來代表每個點到邊界 $(y_n$

( w T z n + b ) = 1 ) (y_{n}(w^{T}z_{n}+b) = 1) 的距離。這樣目標函式和限制條件都做了對應改變，整個問題又變成一個二次規劃可解的問題。

其中變數 $C$代表的是對於比較大的邊際以及比較小的分錯距離的tradeoff。這個問題最終是一個 $\widehat{d}+1+N$個變數， $2N$個限制條件的QP問題。

Dual Problem

同樣的，這個QP問題也有它的拉格朗日對偶問題，推導的過程與Hard-Margin時候的過程類似。

先用拉格朗日乘子把限制條件寫到目標函式裡，然後用maxmin的結果來代替minmax對應的結果，最終滿足KKT條件時兩個結果同時最優。

首先在括號裡對 $\xi$求導得到拉格朗日系數之間的關係 $C-\alpha_{n}-\beta_{n}=0$。這樣就能把係數 $\beta_{n}$替換掉。代入目標式子發現 $\xi$變數係數為0，也能不考慮這個變量了。

依然繼續求導，對係數 $w$和 $b$求導也得到對應的約束條件。

這樣就得到了最後的soft-margin問題的對偶形式：

變成了一個帶有 $N$個變數和 $2N+1$個限制條件的凸QP問題。而且與hard-margin的對偶問題幾乎沒有區別，除了係數 $\alpha_{n}$多了上限的限制。

Messages behind Soft-Margin SVM

把核函式方法也應用到其中，限制得到對應的演算法流程為：

幾乎與hard-margin時候一樣，但是比hard-margin時候更靈活。但是還剩下其中第三步係數 $b$的求解還沒有得到。

來看一下在這個問題裡如何得到係數b：

先回顧一些hard-margin的時候，我們對於support vector有一個對應的限制條件，在知道係數 $\alpha_{s}>0$時對應的支援向量的時候就能夠得到係數b。但是在soft-margin裡要複雜一些。雖然支援向量對應的 $\alpha_{s} > 0$的情況依然有一個等式，但是等式中還有個未知變數 $\xi_{s}$。但是soft-margin裡還多了一個限制條件，如果我們能夠找到 $\alpha_{s}$對應的點，那麼 $xi_{s}$就能夠去掉，得到一個具體的解。但是如果不存在 $\alpha_{s}<C$，那麼最終的b會是一個可行的範圍。

觀察一下使用了高斯核的soft-margin SVM演算法的分類效果。

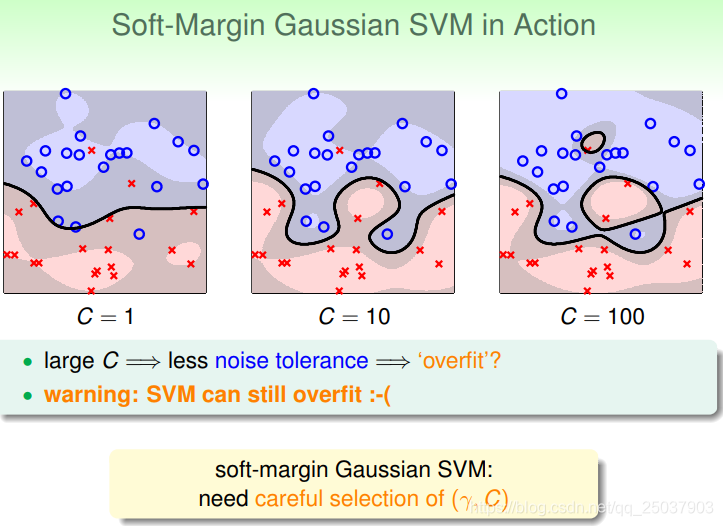
可以看到對於C的調整會增大模型overfit的可能性。因為C越大對應的它對於margin voilation的容忍度就越小，就會導致模型結果越複雜。因此即使是soft-margin也有過擬合的風險，因此還是需要仔細的調參。

有兩個關於鬆弛變數的限制條件，能夠看出其對應的不同的樣本點：

其中，如果 $\alpha_{n}=0$，那麼對應的 $\xi_{n}=0$，也就是這個點是完全分對的，分佈在分類界限分對的一邊。

對於 $0 < \alpha_{n} < C$的情況，對應的 $\xi_{n} = 0$，表明這是個支援向量，而且正好落在分類界限上。

而對於 $\alpha_{n}=C$的情況， $\xi_{n}>=0$，也就是這個點會落在兩條邊界之內，對應的 $\xi_{n}$就是它到己方邊界的距離。

Model Selection

因為實際使用時依然有可能過擬合，因此還需要進行一些模型的選擇：

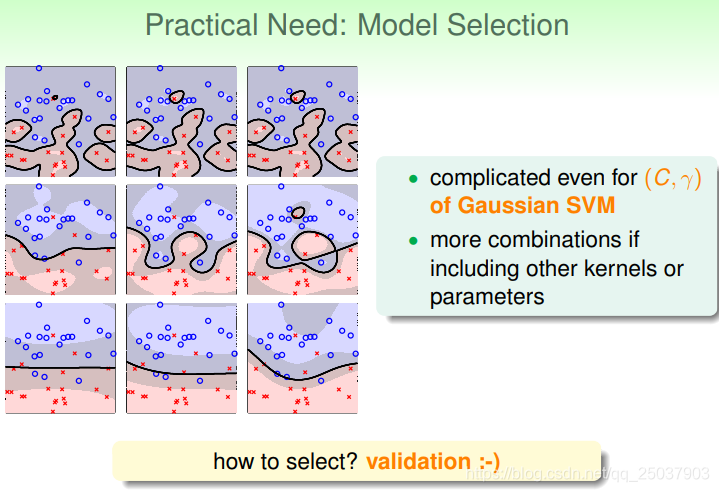
我們可以使用交叉驗證的方式來選擇模型。因為 $E_{cv}(C,\gamma)$是個無法直接優化的問題，因此只能直接進行比較。常用的是使用V-fold驗證的方法。

在這裡有一個假設，那就是留一法交叉驗證的結果會小於等於支援向量所佔的比例：

可以來證明這個命題。假如留一法留下做驗證的那個點不是支援向量，那麼這個點就不會影響到結果，也就是 $g^{-}=g$，因此在這個點上兩個模型都會將其分對。 $e_{non-SV}=err(g^{-},non-SV) = err(g,non-SV) = 0$，而且對於支援向量來說每個點貢獻的 $e_{sv} \leq 1$，也就是說分錯的 $E_{in}$加起來的結果也會小於等於支援向量所佔的比例。

但是這樣一個命題只是說明了交叉驗證時候的一個上限，有時候無法直接判斷出結果：

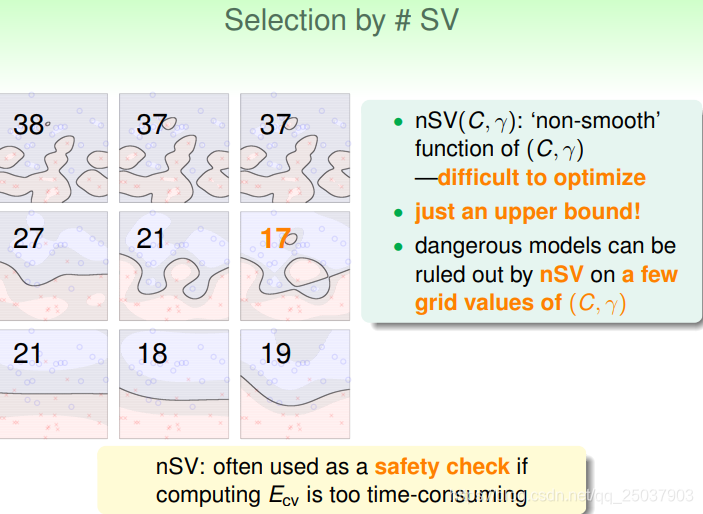
但是根據上限也可以去除掉一些明顯錯誤率偏高的模型。