【YOLOV2】K-means 計算 anchor boxes
目錄
k-means原理
K-means演算法是很典型的基於距離的聚類演算法,採用距離作為相似性的評價指標,即認為兩個物件的距離越近,其相似度就越大。該演算法認為簇是由距離靠近的物件組成的,因此把得到緊湊且獨立的簇作為最終目標。
問題
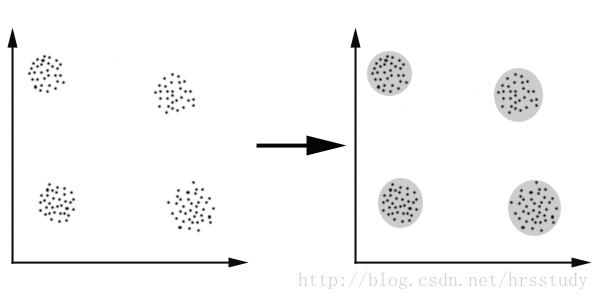
K-Means演算法主要解決的問題如下圖所示。我們可以看到,在圖的左邊有一些點,我們用肉眼可以看出來有四個點群,K-Means演算法被用來找出這幾個點群。
演算法概要

從上圖中,我們可以看到,A, B, C, D, E 是五個在圖中點。而灰色的點是我們的種子點,也就是我們用來找點群的點。有兩個種子點,所以K=2。
然後,K-Means的演算法如下:
隨機在圖中取K(這裡K=2)個種子點。
然後對圖中的所有點求到這K個種子點的距離,假如點Pi離種子點Si最近,那麼Pi屬於Si點群。(上圖中,我們可以看到A,B屬於上面的種子點,C,D,E屬於下面中部的種子點)
接下來,我們要移動種子點到屬於他的“點群”的中心。(見圖上的第三步)
然後重複第2)和第3)步,直到,種子點沒有移動(我們可以看到圖中的第四步上面的種子點聚合了A,B,C,下面的種子點聚合了D,E)。
k-means演算法缺點
1、需要提前指定k
2、k-means演算法對種子點的初始化非常敏感
k-means++演算法
k-means++是選擇初始種子點的一種演算法,其基本思想是:初始的聚類中心之間的相互距離要儘可能的遠。
方法如下:
1.從輸入的資料點集合中隨機選擇一個點作為第一個聚類中心
2.對於資料集中的每一個點x,計算它與最近聚類中心(指已選擇的聚類中心)的距離D(x)
3.選擇一個新的資料點作為新的聚類中心,選擇的原則是:D(x)較大的點,被選取作為聚類中心的概率較大
4.重複2和3直到k個聚類中心被選出來
5.利用這k個初始的聚類中心來執行標準的k-means演算法
第2、3步選擇新點的方法如下:
a.對於每個點,我們都計算其和最近的一個“種子點”的距離D(x)並儲存在一個數組裡,然後把這些距離加起來得到Sum(D(x))。
b.然後,再取一個隨機值,用權重的方式來取計算下一個“種子點”。這個演算法的實現是,先用Sum(D(x))乘以隨機值Random得到值r,然後用currSum += D(x),直到其currSum>r,此時的點就是下一個“種子點”。原因見下圖:

假設A、B、C、D的D(x)如上圖所示,當演算法取值Sum(D(x))*random時,該值會以較大的概率落入D(x)較大的區間內,所以對應的點會以較大的概率被選中作為新的聚類中心。
k-means 計算 anchor boxes
根據YOLOv2的論文,YOLOv2使用anchor boxes來預測bounding boxes的座標。YOLOv2使用的anchor boxes和Faster R-CNN不同,不是手選的先驗框,而是通過k-means得到的。
YOLO的標記檔案格式如下:
<object-class> <x> <y> <width> <height>object-class是類的索引,後面的4個值都是相對於整張圖片的比例。
x是ROI中心的x座標,y是ROI中心的y座標,width是ROI的寬,height是ROI的高。
卷積神經網路具有平移不變性,且anchor boxes的位置被每個柵格固定,因此我們只需要通過k-means計算出anchor boxes的width和height即可,即object-class,x,y三個值我們不需要。
由於從標記檔案的width,height計算出的anchor boxes的width和height都是相對於整張圖片的比例,而YOLOv2通過anchor boxes直接預測bounding boxes的座標時,座標是相對於柵格邊長的比例(0到1之間),因此要將anchor boxes的width和height也轉換為相對於柵格邊長的比例。轉換公式如下:
w=anchor_width*input_width/downsamples
h=anchor_height*input_height/downsamples例如:
卷積神經網路的輸入為416*416時,YOLOv2網路的降取樣倍率為32,假如k-means計算得到一個anchor box的anchor_width=0.2,anchor_height=0.6,則:
w=0.2*416/32=0.2*13=2.6
h=0.6*416/32=0.6*13=7.8距離公式
因為使用歐氏距離會讓大的bounding boxes比小的bounding boxes產生更多的error,而我們希望能通過anchor boxes獲得好的IOU scores,並且IOU scores是與box的尺寸無關的。
為此作者定義了新的距離公式:
d(box,centroid)=1−IOU(box,centroid)在計算anchor boxes時我們將所有boxes中心點的x,y座標都置為0,這樣所有的boxes都處在相同的位置上,方便我們通過新距離公式計算boxes之間的相似度。
程式碼實現
計算anchor boxes的python工具已上傳至GitHub:
https://github.com/PaulChongPeng/darknet/blob/master/tools/k_means_yolo.py
k_means_yolo.py程式碼如下:
# coding=utf-8
# k-means ++ for YOLOv2 anchors
# 通過k-means ++ 演算法獲取YOLOv2需要的anchors的尺寸
import numpy as np
# 定義Box類,描述bounding box的座標
class Box():
def __init__(self, x, y, w, h):
self.x = x
self.y = y
self.w = w
self.h = h
# 計算兩個box在某個軸上的重疊部分
# x1是box1的中心在該軸上的座標
# len1是box1在該軸上的長度
# x2是box2的中心在該軸上的座標
# len2是box2在該軸上的長度
# 返回值是該軸上重疊的長度
def overlap(x1, len1, x2, len2):
len1_half = len1 / 2
len2_half = len2 / 2
left = max(x1 - len1_half, x2 - len2_half)
right = min(x1 + len1_half, x2 + len2_half)
return right - left
# 計算box a 和box b 的交集面積
# a和b都是Box型別例項
# 返回值area是box a 和box b 的交集面積
def box_intersection(a, b):
w = overlap(a.x, a.w, b.x, b.w)
h = overlap(a.y, a.h, b.y, b.h)
if w < 0 or h < 0:
return 0
area = w * h
return area
# 計算 box a 和 box b 的並集面積
# a和b都是Box型別例項
# 返回值u是box a 和box b 的並集面積
def box_union(a, b):
i = box_intersection(a, b)
u = a.w * a.h + b.w * b.h - i
return u
# 計算 box a 和 box b 的 iou
# a和b都是Box型別例項
# 返回值是box a 和box b 的iou
def box_iou(a, b):
return box_intersection(a, b) / box_union(a, b)
# 使用k-means ++ 初始化 centroids,減少隨機初始化的centroids對最終結果的影響
# boxes是所有bounding boxes的Box物件列表
# n_anchors是k-means的k值
# 返回值centroids 是初始化的n_anchors個centroid
def init_centroids(boxes,n_anchors):
centroids = []
boxes_num = len(boxes)
centroid_index = np.random.choice(boxes_num, 1)
centroids.append(boxes[centroid_index])
print(centroids[0].w,centroids[0].h)
for centroid_index in range(0,n_anchors-1):
sum_distance = 0
distance_thresh = 0
distance_list = []
cur_sum = 0
for box in boxes:
min_distance = 1
for centroid_i, centroid in enumerate(centroids):
distance = (1 - box_iou(box, centroid))
if distance < min_distance:
min_distance = distance
sum_distance += min_distance
distance_list.append(min_distance)
distance_thresh = sum_distance*np.random.random()
for i in range(0,boxes_num):
cur_sum += distance_list[i]
if cur_sum > distance_thresh:
centroids.append(boxes[i])
print(boxes[i].w, boxes[i].h)
break
return centroids
# 進行 k-means 計算新的centroids
# boxes是所有bounding boxes的Box物件列表
# n_anchors是k-means的k值
# centroids是所有簇的中心
# 返回值new_centroids 是計算出的新簇中心
# 返回值groups是n_anchors個簇包含的boxes的列表
# 返回值loss是所有box距離所屬的最近的centroid的距離的和
def do_kmeans(n_anchors, boxes, centroids):
loss = 0
groups = []
new_centroids = []
for i in range(n_anchors):
groups.append([])
new_centroids.append(Box(0, 0, 0, 0))
for box in boxes:
min_distance = 1
group_index = 0
for centroid_index, centroid in enumerate(centroids):
distance = (1 - box_iou(box, centroid))
if distance < min_distance:
min_distance = distance
group_index = centroid_index
groups[group_index].append(box)
loss += min_distance
new_centroids[group_index].w += box.w
new_centroids[group_index].h += box.h
for i in range(n_anchors):
new_centroids[i].w /= len(groups[i]) #這裡涉及到了距離的跟新,作者直接使用平均w作為新的寬
new_centroids[i].h /= len(groups[i])
return new_centroids, groups, loss
# 計算給定bounding boxes的n_anchors數量的centroids
# label_path是訓練集列表檔案地址
# n_anchors 是anchors的數量
# loss_convergence是允許的loss的最小變化值
# grid_size * grid_size 是柵格數量
# iterations_num是最大迭代次數
# plus = 1時啟用k means ++ 初始化centroids
def compute_centroids(label_path,n_anchors,loss_convergence,grid_size,iterations_num,plus):
boxes = []
label_files = []
f = open(label_path)
for line in f:
label_path = line.rstrip().replace('images', 'labels')
label_path = label_path.replace('JPEGImages', 'labels')
label_path = label_path.replace('.jpg', '.txt')
label_path = label_path.replace('.JPEG', '.txt')
label_files.append(label_path)
f.close()
for label_file in label_files:
f = open(label_file)
for line in f:
temp = line.strip().split(" ")
if len(temp) > 1:
boxes.append(Box(0, 0, float(temp[3]), float(temp[4])))
if plus:
centroids = init_centroids(boxes, n_anchors)
else:
centroid_indices = np.random.choice(len(boxes), n_anchors)
centroids = []
for centroid_index in centroid_indices:
centroids.append(boxes[centroid_index])
# iterate k-means
centroids, groups, old_loss = do_kmeans(n_anchors, boxes, centroids)
iterations = 1
while (True):
centroids, groups, loss = do_kmeans(n_anchors, boxes, centroids)
iterations = iterations + 1
print("loss = %f" % loss)
if abs(old_loss - loss) < loss_convergence or iterations > iterations_num:
break
old_loss = loss
for centroid in centroids:
print(centroid.w * grid_size, centroid.h * grid_size)
# print result
for centroid in centroids:
print("k-means result:\n")
print(centroid.w * grid_size, centroid.h * grid_size)
label_path = "/raid/pengchong_data/Data/Lists/paul_train.txt"
n_anchors = 5
loss_convergence = 1e-6
grid_size = 13
iterations_num = 100
plus = 0
compute_centroids(label_path,n_anchors,loss_convergence,grid_size,iterations_num,plus)參考
http://coolshell.cn/articles/7779.html
http://www.cnblogs.com/shelocks/
https://blog.csdn.net/hrsstudy/article/details/71173305?utm_source=itdadao&utm_medium=referral
