P3722 [AH2017/HNOI2017]影魔

題解：

法一：

[bzoj4826][HNOI2017]影魔

直接轉化成區間內單點的貢獻，

分開p1,p2考慮

而min(ai,aj),max(ai,aj)要考慮固定一個點、

對於p1,固定i為較小值。發現，這個j只有L[i]或R[i]滿足。

對於p2，差分。找j滿足max(j+1~i-1)<max(ai,aj)

固定i為較大值。發現，這個j的範圍是[L[i]+1,i-1],或者[i+1,R[i]-1]。

具體處理詢問的時候，對邊界l,r取min，取max即可。（見上面的部落格）

發現列出來的式子，

區間、統計小於某個數的個數/這些數的總和，主席樹即可。

細節處理好即可。

程式碼：

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define numb (ch^'0')
#define mid ((l+r)>>1)
using namespace std;
typedef long long ll;
il void rd(int &x){
    char ch;x=0;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true
 
);
    for(x=numb;isdigit(ch=getchar());x=x*10+numb);
    (fl==true)&&(x=-x);
}
namespace Miracle{
const int N=200000+5;
int n,m;
int a[N],le[N],ri[N];
int sta[N],top;
struct segmenttree{
    ll sum[N*20],sz[N*20];
    int ls[N*20],rs[N*20];
    int rt[N];
    int cnt;
    void ins(int &x,int y,int
 
 l,int r,int c){
        x=++cnt;
        sum[x]=sum[y]+c;sz[x]=sz[y]+1;
        ls[x]=ls[y],rs[x]=rs[y];
        if(l==r)return;
        if(c<=mid) ins(ls[x],ls[y],l,mid,c);
        else ins(rs[x],rs[y],mid+1,r,c);        
    }
    ll ql(int x,int y,int l,int r,int c){//num >= c
        int d=sz[x]-sz[y];
        if(!d) return 0;
        if(l==r) return d*(l>=c);
        if(mid>=c) return sz[rs[x]]-sz[rs[y]]+ql(ls[x],ls[y],l,mid,c);
        else return ql(rs[x],rs[y],mid+1,r,c);
    }
    ll qr(int x,int y,int l,int r,int c){//num <= c
        int d=sz[x]-sz[y];
        if(!d) return 0;
        if(l==r) return d*(r<=c);
        if(mid<c) return sz[ls[x]]-sz[ls[y]]+qr(rs[x],rs[y],mid+1,r,c);
        else return qr(ls[x],ls[y],l,mid,c); 
    }
    ll qmin(int x,int y,int l,int r,int c){
        int d=sz[x]-sz[y];
        if(!d) return 0;
        if(l==r) return d*min(l,c);
        if(mid>=c) return (sz[rs[x]]-sz[rs[y]])*c+qmin(ls[x],ls[y],l,mid,c);
        else return sum[ls[x]]-sum[ls[y]]+qmin(rs[x],rs[y],mid+1,r,c);
    }
    ll qmax(int x,int y,int l,int r,int c){
        int d=sz[x]-sz[y];
        if(!d) return 0;
        if(l==r) return d*max(r,c);
        if(mid<c) return (sz[ls[x]]-sz[ls[y]])*c+qmax(rs[x],rs[y],mid+1,r,c);
        else return sum[rs[x]]-sum[rs[y]]+qmax(ls[x],ls[y],l,mid,c);
    }
}L,R;
int p1,p2;
int main(){
    rd(n);rd(m);rd(p1);rd(p2);
    for(reg i=1;i<=n;++i) rd(a[i]);
    for(reg i=1;i<=n;++i){
        while(top&&a[sta[top]]<a[i]) ri[sta[top--]]=i;
        sta[++top]=i;
    }
    while(top) ri[sta[top--]]=n+1;
    for(reg i=n;i>=1;--i){
        while(top&&a[sta[top]]<a[i]) le[sta[top--]]=i;
        sta[++top]=i;
    }
    while(top) le[sta[top--]]=0;
    for(reg i=1;i<=n;++i){
        ++le[i],++ri[i];//warning!!!
        //cout<<i<<" : "<<le[i]<<" "<<ri[i]<<endl;
        L.ins(L.rt[i],L.rt[i-1],1,n+2,le[i]);
        R.ins(R.rt[i],R.rt[i-1],1,n+2,ri[i]);
    }
    int l,r;
    while(m--){
        rd(l);rd(r);
        ll t1=L.ql(L.rt[r],L.rt[l-1],1,n+2,l+1)+R.qr(R.rt[r],R.rt[l-1],1,n+2,r+1);
        //cout<<" t1 "<<t1<<endl;
        ll t2=R.qmin(R.rt[r],R.rt[l-1],1,n+2,r+2)-L.qmax(L.rt[r],L.rt[l-1],1,n+2,l)-2*(r-l+1);
        printf("%lld\n",t1*p1+(t2-t1)*p2);
    }
    return 0;
}

}
int main(){
    Miracle::main();
    return 0;
}

/*
   Author: *Miracle*
   Date: 2018/12/8 19:27:35
*/

法二：

[Hnoi2017]影魔 （單調棧+掃描線+線段樹）

這個還是比較有意思的。雖然不如法一優秀。（離線演算法，而且還難寫）

還是考慮貢獻。

但是這次我們不列舉端點，我們列舉c，也就是[i+1,j-1]的最大值

那麼，對於i，考慮i作為這個最大值的能貢獻出的數對具體是哪些。（注意，具體是哪些，法一我們只關心個數，但是法二要考慮是哪些位置）

對於p1，發現就貢獻一個數對(L[i],R[i])（當然，(i,i+1)不會考慮到，要特殊處理）

對於p2，發現，貢獻([L[i]+1,i-1],R[i])以及(L[i],[i+1,R[i]-1])這些數對。

（證明不重不漏的話，每個數對在列舉到中間的最大值的時候都會考慮到）

然後，數對抽象成平面直角座標系中的一個點

（圖片來自上面部落格）

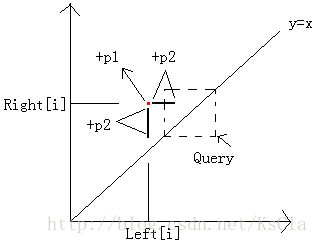
滿足條件的加入的點就是一些點和線段

發現，詢問其實是求位於x屬於[l,r],y屬於[l,r]的點的個數。

離線差分線段樹掃描線即可。

這個轉化還是很漂亮的。（以前一直在找把區間點對(l,r)抽象成直角座標系中點的問題。。）

法一法二的共同思路：

考慮每個點的貢獻。

法一列舉點對的端點

法二列舉點對之間最大值的位置。

對於不同的列舉有不同的處理方法。

對於這種區間點對問題，經常是考慮每個點的貢獻，

並且在列舉的時候，由於比較靈活，所以可以在加上一些欽定

（常用的是靠右的點，但是這個題的話，就不好考慮相對大小關係了，所以欽定是較小值較大值最大值）

如果像這個題還要詢問，那麼就考慮把一個點的貢獻縮成一個值，然後用支援區間查詢的資料結構維護一下。

當然詢問離線也是常用的方法。