There is a public bike service in Hangzhou City which provides great convenience to the tourists from all over the world. One may rent a bike at any station and return it to any other stations in the city.

The Public Bike Management Center (PBMC) keeps monitoring the real-time capacity of all the stations. A station is said to be in perfect

When a problem station is reported, PBMC will always choose the shortest path to reach that station. If there are more than one shortest path, the one that requires the least number of bikes sent from PBMC will be chosen.

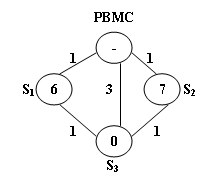
The above figure illustrates an example. The stations are represented by vertices and the roads correspond to the edges. The number on an edge is the time taken to reach one end station from another. The number written inside a vertex S is the current number of bikes stored at S. Given that the maximum capacity of each station is 10. To solve the problem at S​3​​, we have 2 different shortest paths:

1. PBMC -> S​1​​ -> S​3​​. In this case, 4 bikes must be sent from PBMC, because we can collect 1 bike from S​1​​ and then take 5 bikes to S​3​​, so that both stations will be in perfect conditions.

2. PBMC -> S​2​​ -> S​3​​. This path requires the same time as path 1, but only 3 bikes sent from PBMC and hence is the one that will be chosen.

Input Specification:

Each input file contains one test case. For each case, the first line contains 4 numbers: C​max​​ (≤100), always an even number, is the maximum capacity of each station; N (≤500), the total number of stations; S​p​​, the index of the problem station (the stations are numbered from 1 to N, and PBMC is represented by the vertex 0); and M, the number of roads. The second line contains N non-negative numbers C​i​​ (i=1,⋯,N) where each C​i​​ is the current number of bikes at S​i​​ respectively. Then M lines follow, each contains 3 numbers: S​i​​, S​j​​, and T​ij​​ which describe the time T​ij​​ taken to move betwen stations S​i​​ and S​j​​. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print your results in one line. First output the number of bikes that PBMC must send. Then after one space, output the path in the format: 0−>S​1​​−>⋯−>S​p​​. Finally after another space, output the number of bikes that we must take back to PBMC after the condition of S​p​​ is adjusted to perfect.

Note that if such a path is not unique, output the one that requires minimum number of bikes that we must take back to PBMC. The judge's data guarantee that such a path is unique.

Sample Input:

10 3 3 5
6 7 0
0 1 1
0 2 1
0 3 3
1 3 1
2 3 1

Sample Output:

3 0->2->3 0

先說 題意： 找到一條從 0 到 的最短路徑， 並且調整從0 到 路上的所有結點使其平衡，（只是從0到的過程中調整，回來不調整）， 如果有多條最短路，我們先選擇，從0點拿出來的最少的方案， 如果這樣的方案還有多條，我們選擇，需要放回0點最少的方案。   

思路：跑一邊最短路，然後直接爆搜。 發現pat,不太卡時間，比較卡情況。

#include<bits/stdc++.h>
using namespace std;

typedef long long LL;

#define rep(i,a,b) for(int i=a;i<b;++i)

const int N=510;
const int INF=0x3f3f3f3f;

struct Node{
	int x,dis;
	Node(int _x=0,int _dis=0):x(_x),dis(_dis){}
	bool operator<(const Node& b)const{
		return dis>b.dis;
	}
};

struct Edge{
	int v,w;
	Edge(int _v=0,int _w=0){
		v=_v,w=_w;
	}
};
vector<Edge>edge[N];

priority_queue<Node> pq;
int dis[N],vis[N],has[N];
void dijistra(int n,int sp,int cx){

	rep(i,0,n+1)dis[i]=INF;
	dis[0]=0;

	Node now,nxt;
	pq.push(Node(0,0));
	while(!pq.empty()){
		now=pq.top();
		pq.pop();
		int u=now.x;
		if(vis[u])continue;
		vis[u]=1;
		for(int i=0;i<edge[u].size();i++){
			Edge e=edge[u][i];
			int v=e.v;
		    if(dis[u]+e.w<dis[v]){
				dis[v]=e.w+dis[u];
				pq.push(Node(e.v,dis[v]));
			}
		}
	}
}

int cx,n,sp,m;
int res_car=INF,res_sum=INF,tot=0;
int res[N],tmp[N];
void dfs(int x,int cnt,int car,int sum){
	if(x==sp){
		if(car<res_car){
			res_car=car;res_sum=sum+car-cnt*cx/2;tot=cnt;
			rep(i,0,cnt+1)res[i]=tmp[i];
		}else if(car==res_car&&sum+car-cnt*cx/2<res_sum){
			res_sum=sum+car-cnt*cx/2; tot=cnt;
			rep(i,0,cnt)res[i]=tmp[i];
		}
		return;
	}
	
	for(int i=0;i<edge[x].size();i++){
		Edge& e=edge[x][i];
		int v=e.v;
		if(!vis[v]&&dis[v]>=dis[x]+e.w){
			
			vis[v]=1;
			int t1=car,t2=sum;
			t2+=has[v];
			
		    int s=(cnt+1)*cx/2; 
			if(t2+t1<s){
				t1+=(s-(t1+t2));
			}
			tmp[cnt]=v;
			dfs(v,cnt+1,t1,t2);
			vis[v]=0;
		}
	}
}
int main(){
	
	scanf("%d %d %d %d",&cx,&n,&sp,&m);

	rep(i,1,n+1)scanf("%d",&has[i]);

	rep(i,0,m){
		int u,v,w;
		scanf("%d %d %d",&u,&v,&w);
		edge[u].push_back(Edge(v,w));
		edge[v].push_back(Edge(u,w));
	}
	
	dijistra(n,sp,cx);
	
	rep(i,0,n+1)vis[i]=0;
	vis[0]=1;
	dfs(0,0,0,0);
	
	printf("%d 0",res_car);
	rep(i,0,tot)printf("->%d",res[i]);
	printf(" %d\n",res_sum);
	return 0;
}