1018 Public Bike Management（30 分）

There is a public bike service in Hangzhou City which provides great convenience to the tourists from all over the world. One may rent a bike at any station and return it to any other stations in the city.

The Public Bike Management Center (PBMC) keeps monitoring the real-time capacity of all the stations. A station is said to be in perfect

 condition if it is exactly half-full. If a station is full or empty, PBMC will collect or send bikes to adjust the condition of that station to perfect. And more, all the stations on the way will be adjusted as well.

When a problem station is reported, PBMC will always choose the shortest path to reach that station. If there are more than one shortest path, the one that requires the least number of bikes sent from PBMC will be chosen.

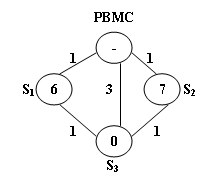
The above figure illustrates an example. The stations are represented by vertices and the roads correspond to the edges. The number on an edge is the time taken to reach one end station from another. The number written inside a vertex S is the current number of bikes stored at S. Given that the maximum capacity of each station is 10. To solve the problem at S​3​​, we have 2 different shortest paths:

1. PBMC -> S​1​​ -> S​3​​. In this case, 4 bikes must be sent from PBMC, because we can collect 1 bike from S​1​​ and then take 5 bikes to S​3​​, so that both stations will be in perfect conditions.

2. PBMC -> S​2​​ -> S​3​​. This path requires the same time as path 1, but only 3 bikes sent from PBMC and hence is the one that will be chosen.

Input Specification:

Each input file contains one test case. For each case, the first line contains 4 numbers: C​max​​ (≤100), always an even number, is the maximum capacity of each station; N (≤500), the total number of stations; S​p​​, the index of the problem station (the stations are numbered from 1 to N, and PBMC is represented by the vertex 0); and M, the number of roads. The second line contains N non-negative numbers C​i​​ (i=1,⋯,N) where each C​i​​ is the current number of bikes at S​i​​ respectively. Then M lines follow, each contains 3 numbers: S​i​​, S​j​​, and T​ij​​ which describe the time T​ij​​ taken to move betwen stations S​i​​ and S​j​​. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print your results in one line. First output the number of bikes that PBMC must send. Then after one space, output the path in the format: 0−>S​1​​−>⋯−>S​p​​. Finally after another space, output the number of bikes that we must take back to PBMC after the condition of S​p​​ is adjusted to perfect.

Note that if such a path is not unique, output the one that requires minimum number of bikes that we must take back to PBMC. The judge's data guarantee that such a path is unique.

Sample Input:

10 3 3 5
6 7 0
0 1 1
0 2 1
0 3 3
1 3 1
2 3 1

Sample Output:

3 0->2->3 0

作者: CHEN, Yue

單位: 浙江大學

時間限制: 400 ms

記憶體限制: 64 MB

程式碼長度限制: 16 KB

題目大意：

在杭州有很多公共自行車，可以從任意車站騎走並歸還到任意車站
我們稱車站的perfect狀態是單車數量恰好為車站容量的一半
如果有車站滿或空，排程中心會派人去運送單車，使得車站狀態達到perfect
同時，沿路上的車站狀態也都會被調整為perfect
排程中心在選擇排程路線時，會選擇從排程中心到達目標車站路程最短的那條路
如果不止一條路程最短的路，排程中心就會選擇搬運單車數量最少的路
如果帶出單車數量最少的路還有多條，就選擇帶回數量最少的一條 
在一行內給出排程中心需要送出多少輛單車，送車的路徑，以及需要送回多少輛車到排程中心

解題思路：

本題不能用直接的Dijkstra演算法解決，因為minNeed和minRemain的傳遞不滿足最優子結構
只有當所有的路徑都確定後，才能去選擇最優的路徑
題目需要在從排程中心出發到達問題點sp的過程中就把路徑上所有節點調整好，此後不再調整
在本題中，路徑長短是第一標尺，帶出單車數量是第二標尺，帶回單車數量是第三標尺
因為是在路徑上遇見一個調整一個節點，所以need和remain有時候會都為正值
比如第一個節點需要補10輛車，你就要把need+=10，第二個節點又要送出20輛，這時候就要把remain+=20
然後進入第三個節點進行處理

總的來說就是先用Dijkstra演算法找最短路徑，全部儲存下來，然後在DFS遍歷中檢查第二和第三標尺，選擇最優路徑

AC程式碼：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<cstring>
#include<cmath>
#include<vector>
#include<stack>
#include<set>
#include<map>
#include<queue>
#include<cctype>
using namespace std;
const int maxn=600;
const int INF=0x3f3f3f3f;
bool vis[maxn];
int d[maxn];
int weight[maxn],w[maxn];
int G[maxn][maxn];
int c,n,sp,m;
int minNeed=INF,minRemain=INF;//最少攜帶和最少帶回數目 
vector<int> pre[maxn];//前驅 
vector<int> tempPath,path;//臨時路徑和最優路徑 
void Dijkstra(int s);
void DFS(int v);
int main()
{
	scanf("%d%d%d%d",&c,&n,&sp,&m);
	fill(G[0],G[0]+maxn*maxn,INF);
	for(int i=1;i<=n;i++)
	{
		//減去c/2，就可以直接從weight[i]的值來判斷需要加入還是帶走多少單車了 
		scanf("%d",&weight[i]);
		weight[i]-=c/2;
	}
	int u,v,dis;
	for(int i=0;i<m;i++)
	{ 
		scanf("%d%d%d",&u,&v,&dis);
		G[u][v]=dis;
		G[v][u]=dis;
	}
	Dijkstra(0);//演算法起點從排程中心開始 
	DFS(sp);
	printf("%d ",minNeed);
	for(int i=path.size()-1;i>=0;i--)
	{
		printf("%d",path[i]);
		if(i>0) printf("->");
	}
	printf(" %d",minRemain);
	return 0;
}

void Dijkstra(int s)
{
	fill(d,d+maxn,INF);
	d[s]=0;
	for(int i=0;i<n;i++)
	{
		int u=-1,MIN=INF;
		for(int j=0;j<=n;j++)
		{
			if(vis[j]==false&&d[j]<MIN)
			{
				u=j;
				MIN=d[j];
			}
		}
		if(u==-1) return;
		vis[u]=true;
		for(int v=0;v<=n;v++)
		{
			if(vis[v]==false&&G[u][v]!=INF)
			{
				if(d[v]>d[u]+G[u][v])//找到更優路線，清空原有方案，記錄新路線 
				{
					d[v]=d[u]+G[u][v];
					pre[v].clear();
					pre[v].push_back(u);
				}
				else if(d[v]==d[u]+G[u][v])//相同優先順序的路線，直接記錄 
					pre[v].push_back(u);
			}
		}
	}
}

void DFS(int v)
{
	if(v==0)//遞迴邊界，葉子節點 
	{
		tempPath.push_back(v);
		int need=0,remain=0;//從排程中心到當前車站必須攜帶的數目，從車站帶回排程中心的數目 
		for(int i=tempPath.size()-1;i>=0;i--)//此處必須倒著列舉 
		{
			int id=tempPath[i];
			if(weight[id]>0)//點權>0，說明需要帶走一部分自行車 
				remain+=weight[id];//當前自行車持有量+weight[id] 
			else
			{//weight為負數時代表需要補給自行車，數量為abs(weight)，如果remain>0就可以用來補給 
				if(remain>abs(weight[id]))//remain足夠用來補給當前車站 
					remain-=abs(weight[id]);//當前持有量減少補給的量 
				else//remain不夠用來補給當前車站 
				{
					need+=abs(weight[id])-remain;//不夠的不分從排程中心攜帶 
					remain=0;//remain全部用來排程之後，把remain置0 
				}
			}
		}
		if(need<minNeed)//如果從排程中心攜帶的單車數量變少 
		{
			minNeed=need;//更新minNeed 
			minRemain=remain;//覆蓋minRemain 
			path=tempPath;//更新最優路徑 
		}
		else if(need==minNeed&&remain<minRemain)//攜帶數目相同，帶回數目變少 
		{
			minRemain=remain;
			path=tempPath;
		}
		tempPath.pop_back();
		return;
	}
	tempPath.push_back(v);
	for(int i=0;i<pre[v].size();i++)
		DFS(pre[v][i]);
	tempPath.pop_back();
}