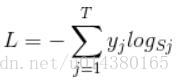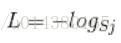2. 程式人生 > >簡明談談softmax loss

簡明談談softmax loss

阿新 • • 發佈：2018-12-09

softmax loss概念如下：

這裡寫圖片描述

首先L是損失。Sj是softmax的輸出向量S的第j個值，前面已經介紹過了，表示的是這個樣本屬於第j個類別的概率。yj前面有個求和符號，j的範圍也是1到類別數T，因此y是一個1*T的向量，裡面的T個值，而且只有1個值是1，其他T-1個值都是0。那麼哪個位置的值是1呢？答案是真實標籤對應的位置的那個值是1，其他都是0。所以這個公式其實有一個更簡單的形式：

這裡寫圖片描述

當然此時要限定j是指向當前樣本的真實標籤。

來舉個例子吧。假設一個5分類問題，然後一個樣本I的標籤y=[0,0,0,1,0]，也就是說樣本I的真實標籤是4，假設模型預測的結果概率（softmax的輸出）p=[0.1,0.15,0.05,0.6

,0.1]，可以看出這個預測是對的，那麼對應的損失L=-log(0.6)，也就是當這個樣本經過這樣的網路引數產生這樣的預測p時，它的損失是-log(0.6)。那麼假設p=[0.15,0.2,0.4,0.1,0.15]，這個預測結果就很離譜了，因為真實標籤是4，而你覺得這個樣本是4的概率只有0.1（遠不如其他概率高，如果是在測試階段，那麼模型就會預測該樣本屬於類別3），對應損失L=-log(0.1)。那麼假設p=[0.05,0.15,0.4,0.3,0.1]，這個預測結果雖然也錯了，但是沒有前面那個那麼離譜，對應的損失L=-log(0.3)。我們知道log函式在輸入小於1的時候是個負數，而且log函式是遞增函式，所以-log(0.6) < -log(0.3) < -log(0.1)。簡單講就是你預測錯比預測對的損失要大，預測錯得離譜比預測錯得輕微的損失要大。

相關推薦

簡明談談softmax loss

softmax loss概念如下： 首先L是損失。Sj是softmax的輸出向量S的第j個值，前面已經介紹過了，表示的是這個樣本屬於第j個類別的概率。yj前面有個求和符號，j的範圍也是1到類別數T，因此y是一個1*T的向量，裡面的T個值，而且只有1個值是1，其他T-1

Softmax vs. Softmax-Loss: Numerical Stability(轉載)

-s .cn .com src org abi com 轉載 image http://freemind.pluskid.org/machine-learning/softmax-vs-softmax-loss-numerical-stability/ Softmax

卷積神經網絡系列之softmax，softmax loss和cross entropy的講解

caff 這一 卷積神經網絡 bsp rop 技術分享 有一個 技術 位置 我們知道卷積神經網絡（CNN）在圖像領域的應用已經非常廣泛了，一般一個CNN網絡主要包含卷積層，池化層（pooling），全連接層，損失層等。雖然現在已經開源了很多深度學習框架（比如MxNet，Ca

【轉載】Softmax vs. Softmax-Loss: Numerical Stability

一切起源於我在 caffe 的網站上看到的關於 SoftmaxLossLayer 的描述： The softmax loss layer computes the multinomial logistic loss of the softmax of its inpu

【技術綜述】一文道盡softmax loss及其變種

本文首發於龍鵬的知乎專欄《有三AI學院》 https://zhuanlan.zhihu.com/c_151876233 今天來說說softmax loss以及它的變種 01 softmax loss softmax loss是我們最熟悉的loss之一了，分

卷積神經網路系列之softmax loss對輸入的求導推導

我們知道卷積神經網路（CNN）在影象領域的應用已經非常廣泛了，一般一個CNN網路主要包含卷積層，池化層（pooling），全連線層，損失層等。雖然現在已經開源了很多深度學習框架（比如MxNet，Caffe等），訓練一個模型變得非常簡單，但是你對損失函式求梯度是怎

問題的轉換(1): center loss, l2-constrained softmax loss, a noise adaption layer

參考文獻: 1.A Discriminative Feature Learning Approach for Deep Face Recognition 2.L2-constrained Sof

卷積神經網路系列之softmax，softmax loss和cross entropy loss的講解

我們知道卷積神經網路（CNN）在影象領域的應用已經非常廣泛了，一般一個CNN網路主要包含卷積層，池化層（pooling），全連線層，損失層等。雖然現在已經開源了很多深度學習框架（比如MxNet，Caffe等），訓練一個模型變得非常簡單，但是你對這些層具體是怎麼實現的瞭解嗎？你對softmax，sof

faster rcnn中 損失函式（一）——softmax，softmax loss和cross entropy的講解

先理清下從全連線層到損失層之間的計算。來看下面這張圖，（非常好的圖）。 T類  N表示前一層特徵層flatten後的數字   fltten後的特徵      無限大小的T類                     從0-1的T類向量                   

人臉識別：損失函式之softmax loss和cross entropy Loss

轉載blog：http://blog.csdn.net/u014380165/article/details/77284921 我們知道卷積神經網路（CNN）在影象領域的應用已經非常廣泛了，一般一個CNN網路主要包含卷積層，池化層（pooling），全連線層，損失層等。

損失函式改進方法之A-softmax loss

深度學習交流QQ群：116270156 論文：SphereFace: Deep Hypersphere Embedding for Face Recognition  論文連結：https://arxiv.org/abs/1704.08063 這篇是CVPR2017的

關於Logistic Regression、Softmax Loss和Cross-entropy的隨筆

最近看深度學習影象分類的相關知識的時候，發現對於Softmax損失函式的相關概念沒有搞明白，因此講設計到的相關知識一些梳理，供大家參考。 本文以CIFAR-10資料集圖片分類任務為例展開，定義第i 個輸入樣本xi ，輸出yi ，圖片共有10類（k=0,1

卷積神經網路系列之softmax，softmax loss和cross entropy的講解

我們知道卷積神經網路（CNN）在影象領域的應用已經非常廣泛了，一般一個CNN網路主要包含卷積層，池化層（pooling），全連線層，損失層等。雖然現在已經開源了很多深度學習框架（比如MxNet，Caffe等），訓練一個模型變得非常簡單，但是你對這些層具體是怎麼實

目標檢測之loss：softmax Loss 梯度推導

1softmax函式softmax用於多分類過程中，它將多個神經元的輸出，對映到（0,1）區間內，可以看成概率來理解，從而來進行多分類！假設我們有一個數組，V，Vi表示V中的第i個元素，那麼這個元素的softmax值就是 si = si/(si+sj+...sk)更形象的如下

Large-Margin Softmax Loss for Convolutional Neural Networks

線性分類 大學 amp ima 困難 訓練 http con network paper url: https://arxiv.org/pdf/1612.02295 year:2017 Introduction 交叉熵損失與softmax一起使用可以說是CNN中最常用的監督

深度學習基礎--loss與啟用函式--sigmiod與softmax；對數損失函式與交叉熵代價函式

sigmiod與softmax   sigmiod就是邏輯迴歸（解決二分類問題）；softmax是多分類問題的邏輯迴歸   雖然邏輯迴歸能夠用於分類，不過其本質還是線性迴歸。它僅線上性迴歸的基礎上，在特徵到結果的對映中加入了一層sigmoid函式（非線性）對映，即先把特徵線性求和，然後使

Softmax&SVM loss&gradient公式圖及其python實現

Softmax與SVM都是用來對資料進行分類的。Softmax常用於神經網路的輸出層，SVM常常直接與SGD配合實現物體分類。無論是Softmax還是SVM在工作時都需要計算出loss和gradient，學習使用中發現兩者有很多相似之處，特拿來對比學習。 公式 圖

簡單談談Cross Entropy Loss

版權宣告：本文為博主原創文章，未經博主允許不得轉載。    https://blog.csdn.net/xg123321123/article/details/80781611 寫在前面 分類問題和迴歸問題是監督學習的兩大種類：分類問題的目標變數是離散的；迴歸問題的目標變數

SVM hinge loss / SoftMax cross entropy loss

損失函式(loss function) = 誤差部分(loss term) + 正則化部分(regularization term) 1. 誤差部分 1.1 gold term,0-1損失函式,記錄分類錯誤的次數 1.2 Hinge loss, 折葉損失,關於

softmax logistic loss詳解

softmax函式–softmax layer softmax用於多分類過程中，它將多個神經元的輸出，對映到（0,1）區間內，可以看成概率來理解，從而來進行多分類！ 假設我們有一個數組z=(z1,z2,...zm),則其softmax函式定義如下： σi(