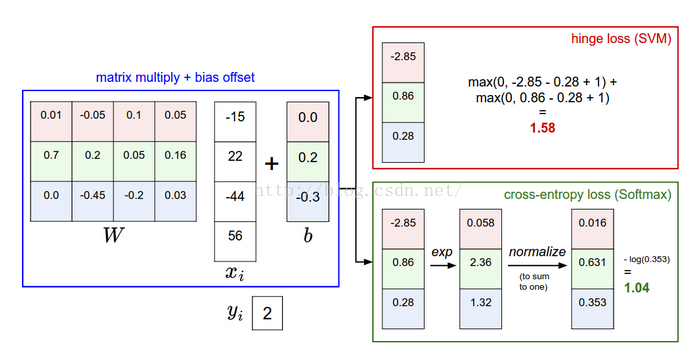
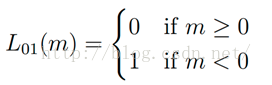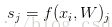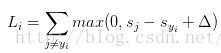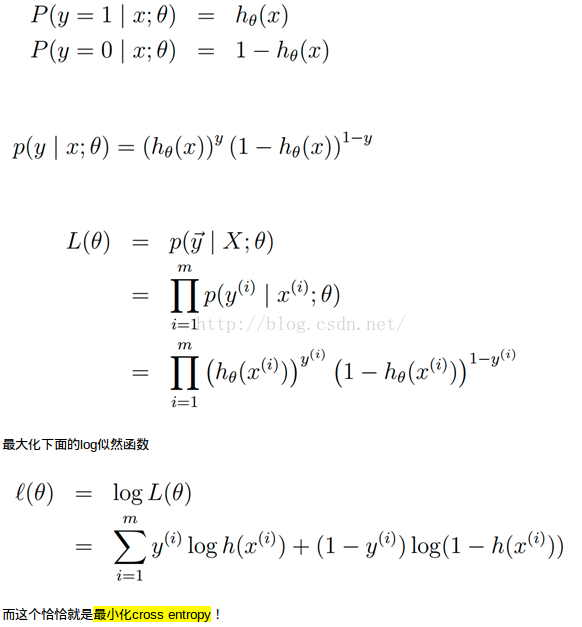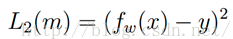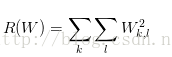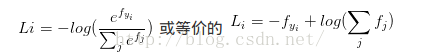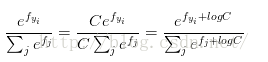SVM hinge loss / SoftMax cross entropy loss
損失函式(loss function) = 誤差部分(loss term) + 正則化部分(regularization term)
1. 誤差部分
1.1 gold term,0-1損失函式,記錄分類錯誤的次數
1.2 Hinge loss, 折葉損失,關於0的閥值
定義:E(z)=max(0,1-z)
應用: SVM中的最大化間隔分類,max-margin loss最大邊界損失
舉例: SVM的損失函式想要SVM在正確分類上的得分始終比不正確分類上的得分高出一個邊界值delta.
比如第i個樣本資料為xi和其正確類別標籤yi, 通過公式f(xi,W)來計算屬於不同類別的分數, 針對第j個類別的得分為
SVM的損失函式想要正確分類類別yi的分數比不正確類別分數高.且至少要高delta.若不滿足這個要求,便計算損失值.
平方折葉損失SVM(L2-SVM),使用的誤差部分為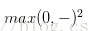
1.3 Log loss
定義:
應用場景: logistic regression,cross entropy error
1.4 squared loss
定義:
應用場景: linear regression
1.5 exponential loss
定義:
應用場景: boosting
2. 正則化部分
若損失函式只包含誤差部分,可能存在多個W;有時希望向某些特定的權重W新增一些偏好,對其它權重則不新增,以此來消除模糊性; 為了解決上述問題, 在誤差部分基礎上新增正則化懲罰(regularization penalty)部分.
最常用的正則化懲罰是L2正規化, L2正規化通過對所有引數進行逐元素的平方懲罰來抑制大數值的權重,公式如下:
正則化部分僅僅基於權重,與資料無關.
正則化最好的性質是對大數值權重進行懲罰,提升模型泛化能力,因為這意味著沒有哪個維度能夠獨自對於整體分值有過大的影響,避免產生過擬合.
**與權重不同,偏差沒有這樣的效果,因為它們並不控制輸入維度上的影響強度,因此正則化部分只針對權重.
***由於正則化部分的存在,不可能所有的例子都能得到0的損失值,這是因為只有當W=0的特殊情況下,損失值才為0.
應用舉例:多分類SVM
其完整損失公式:
SVM損失函式採用了一種特殊的方法使得能夠衡量對於訓練資料分類和實際分類標籤的一致性.
設定delta: 超引數delta在絕大多數情況下設為0.1,超引數delta和lamda看起來是兩個不同的超引數,但實際上它們一起控制同一個權衡: 損失函式中的資料損失和正則化損失之間的權衡; 當將W中值縮小,分類分值之間的差異也變小,反之亦然; 因此, 不同分類分值之間的邊界的具體值delta=1或delta-100從某些角度是沒有意義的,因為權重就可以控制差異變大和縮小.即真正的權衡是允許權重能夠變大到何種程度,通過正則化強度lamda來控制.
多分類SVM和二元SVM的關係:
二元SVM對第i個數據的損失計算公式為:
此公式是多分類公式只有2個類別的特例, 這裡的C和多類SVM公式中的lamda控制著同樣的權衡,即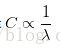
多類SVM有多種損失函式,這裡只是其中一種;
One-VS-ALL(OVA)SVM: 針對每個類和其他類訓練一個獨立的二元分類器,常用.
All-vs-All(AVA) SVM: 很少用
structured SVM: 將正確分類的分類分值和非正確分類中的最高分值的邊界最大化
SVM和Softmax分類器是最常用的兩個分類器.
Softmax分類器可以理解為邏輯迴歸分類器面對多個分類的一般話歸納.
1.SVM將輸出作為對每個分類的評分(沒有規定的標準,難以直接解釋);
2. softmax的輸出(歸一化的分類概率)更加直觀,且可以從概率上解釋.
在Softmax分類器中, 函式對映保持不變,但將這些評分值看做每個分類未歸一化的對數概率,且將折葉損失替換為交叉熵損失(cross-entropy loss),公式如下:
表示分類評分向量f中的第i個元素,和SVM一樣,整個資料集的損失值是資料集中所有樣本資料的損失值Li的均值和正則化損失之和.
概率論解釋:
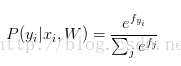
實際操作注意事項:數值穩定:程式設計實現softmax函式計算的時候,中間項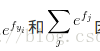
C的值可自由選擇,不會影響計算結果,通過這個技巧可以提高計算中的數值穩定性.通常將C設為: 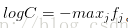
該技巧就是將向量f中的數值進行平移,使得最大值為0.
SVM/Softmax的比較
Softmax分類器為每個分類器提供了"可能性":SVM的計算是無標定的,且難以針對所有分類的評分值給出直觀解釋;softmax分類器不同,它允許計算出對於所有分類標籤的可能性.
實際使用中, SVM和Softmax是很相似的,一般地,兩者的表現差別很小;
但是想對於softmax,SVM更加區域性目標化,這既是一個特點,也是一個劣勢;考慮一個評分是[10,-2,3]的資料,其中第一個分類是正確的,那麼SVM(delta=1)會看到正確分類相對於不正確分類的差值已經比邊界值要高,因此損失值為0,SVM對於數字個體細節不care,[10,-100,-100]或[10,9,9],對SVM沒有差,因為只要差值超過邊界值,那麼損失值為0.
對於softmax分類器,對於[10,9,9]而言,計算出的損失值遠遠高於[10,-100,-100].換言之,softmax分類器對於分數永遠不會滿意;正確分類總能得到更高的可能性,錯誤分類總能得到更低的可能性,損失值總是能夠更小.
SVM只要邊界值滿足就滿意了,不會超過限制去細微地操作具體分數.
參考:https://zhuanlan.zhihu.com/p/21102293?refer=intelligentunit