解讀CTC LOSS原理
為什麼要使用CTC(Connectionist temporal classification):
在傳統的語音識別的聲學模型訓練中,對於每一幀的資料,我們需要知道對應的label才能進行有效的訓練,在訓練資料之前需要做語音對齊的預處理。對齊的預處理要花費大量的人力和時間,而且對齊之後,模型預測出的label只是區域性分類的結果,而無法給出整個序列的輸出結果,往往要對預測出的label做一些後處理才可以得到我們最終想要的結果。
如:

上圖是“你好”這句話的聲音的波形示意圖, 每個紅色的框代表一幀資料,傳統的方法需要知道每一幀的資料是對應哪個發音音素。比如第1,2,3,4幀對應n的發音,第5,6,7幀對應i的音素,第8,9幀對應h的音素,第10,11幀對應a的音素,第12幀對應o的音素。(這裡暫且將每個字母作為一個發音音素)
我們能不能讓我們的神經網路自己去學習對齊方式呢?
CTC(Connectionist temporal classification,連線時序分類)就是為了解決這個問題。
與傳統的聲學模型訓練相比,採用CTC作為損失函式的聲學模型訓練,是一種完全端到端的聲學模型訓練,不需要預先對資料做對齊,只需要一個輸入序列和一個輸出序列即可以訓練。這樣就不需要對資料對齊和一一標註,並且CTC直接輸出序列預測的概率,不需要外部的後處理。
CTC的方法是關心一個輸入序列到一個輸出序列的結果,那麼它只關心預測輸出的序列是否和真實的序列是否接近(相同),而不會關心預測輸出序列中每個結果在時間點上是否和輸入的序列正好對齊。
CTC引入了blank(該幀沒有預測值),每個預測的分類對應的一整段語音中的一個spike(尖峰),其他不是尖峰的位置認為是blank。對於一段語音,CTC最後的輸出是spike(尖峰)的序列,並不關心每一個音素持續了多長時間。
對一段音訊使用文字對齊和使用CTC的例子:

上圖中首行是原始的音訊資料,陰影線是在特定時間觀察音素的概率對應的輸出啟用。中間行是使用了文字對齊的方法(Framewise方法),即對每個音素做標記 (對輸入序列的每個時間步長或幀進行獨立標記) 。最後一行是CTC方法,CTC並不需要這樣的標記,而是預測了一系列峰值 (spikes),緊接著一些空白 (blanks)用來區分字母。我們可以看到基於Framewise的方法出現了 misallignling segment boundaries error(錯誤的分段邊界錯誤)。就是說兩個因素的label的概率分佈圖太近了, 比如在發音 dh, dh 和ax 有明顯重疊,而CTC的方法卻沒有出現這種現象。
CTC網路的計算:
論文:Connectionist Temporal Classification: Labelling Unsegmented Sequence Data with Recurrent Neural Networks
論文地址:http://people.idsia.ch/~santiago/papers/icml2006.pdf
另外有一個網站上也很好地闡述了CTC的原理:https://distill.pub/2017/ctc/
一個CTC網路有一個softmax輸出層,除了序列的輸出外,還增加了一個額外的輸出單元,最開始激勵的|L|個單元被解釋成在這個時刻對應標籤的觀察概率,激勵的額外的單元是一個空白的觀察概率或者無標籤的觀察概率。這些輸出定義為在給定輸入序列的情況下,所有可能的對齊所有標記序列的方式。標記序列的概率是所有可能對齊方式的概率和。
輸入序列x,長度為T,定義一個RNN,有m個輸入,n個輸出,權重向量w作為一個連續對映![]() 。
。
假如序列目標為字串(詞表大小為 n),即 Nw 輸出為 n 維多項概率分佈。
令![]() 為網路的序列輸出,
為網路的序列輸出,![]() 是單元k在時刻t的激勵。
是單元k在時刻t的激勵。![]() 解釋為輸出序列在第t個時間步輸出為k的概率。
解釋為輸出序列在第t個時間步輸出為k的概率。
如:當輸出的序列為(a-ab-)時,![]() 代表了在第3步輸出的字母為a的概率。
代表了在第3步輸出的字母為a的概率。
這定義了一個在集合![]() 的長度為T的序列分佈,L’=L+{blank}:
的長度為T的序列分佈,L’=L+{blank}:
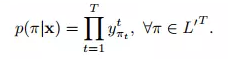
![]() 是所有路徑的集合,π表示其中的一個路徑。上式中隱含有一個假設,給定網路的內部狀態,網路在不同時刻的輸出是條件獨立的。
是所有路徑的集合,π表示其中的一個路徑。上式中隱含有一個假設,給定網路的內部狀態,網路在不同時刻的輸出是條件獨立的。![]() 代表了給定輸入x,輸出路徑為 π 的概率,由於假設在每一個時間步輸出的label的概率都是相互獨立的,那麼
代表了給定輸入x,輸出路徑為 π 的概率,由於假設在每一個時間步輸出的label的概率都是相互獨立的,那麼 ![]() ,可以理解為每一個時間步輸出路徑π的相應label的概率的乘積。
,可以理解為每一個時間步輸出路徑π的相應label的概率的乘積。
下一步是定義多到一的對映β:
序列學習任務一般而言是多對多的對映關係(如語音識別中,上百幀輸出可能僅對應若干音節或字元,並且每個輸入和輸出之間,也沒有清楚的對應關係)。CTC 通過引入一個特殊的 blank 字元(用 % 表示),解決多對一對映問題。
擴充套件原始詞表L為 L′=L∪{blank}。定義多對一對映β![]() ,
,![]() 是可能標記的集合。
是可能標記的集合。
β對映可以認為是將輸出路徑π對映到標籤序列L的一種變換。集合中定義操作:合併連續的相同字元;去掉 blank 字元。
如:![]() (其中-代表了空格)
(其中-代表了空格)
上面兩種B都代表字元aab。
最終,β定義為一個給定序列L屬於![]() 的條件概率,條件概率是所有路徑的概率和。
的條件概率,條件概率是所有路徑的概率和。
通過引入blank 及β,可以實現變長的對映: ![]() ,也因為這個原因,CTC 只能建模輸出長度小於輸入長度的序列問題。
,也因為這個原因,CTC 只能建模輸出長度小於輸入長度的序列問題。
和大多數有監督學習一樣,CTC 使用最大似然估計進行訓練。
給定輸入x,輸出L的條件概率為:
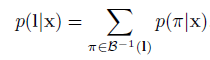
B−1(l) 表示了長度為T 且示經過B結果為L字串的集合。![]() 代表給定輸入x,輸出為序列L的概率。
代表給定輸入x,輸出為序列L的概率。
CTC 假設輸出的概率是(相對於輸入)條件獨立的,因此有:
![]()
然而,直接按上式我們沒法有效計算似然值。我們可以用動態規劃解決似然的計算及梯度計算, 涉及前向演算法和後向演算法。請看後面的前向和後向演算法部分。
構造分類器:
分類器的輸出應該是在給定輸入序列下的最可能的標記輸出:
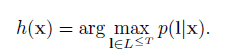
利用HMMs演算法,我們把尋找這個標記的過程記為解碼,但是我們找不到一個通用並且tractable的解碼演算法。
下面是兩個近似的演算法,在實踐中給出了良好的結果。
最佳路徑解碼(best path decoding):
基於的假設:最可能的路徑會對應最可能的標籤。
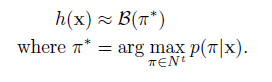
最佳路徑解碼非常容易計算,π*僅僅就是每個時間步的最可能的輸出的連線。但是它不能保證找到最有可能的標記。
字首查詢解碼(prefix search decoding):
這個方法據說給定足夠的計算資源和時間, 能找到最優解。 但是複雜度會隨著輸入sequence長度的變化呈指數增長。這裡推薦用有限長度的prefix search decode 來做。 但是具體考慮多長的sequence做判斷還需具體問題具體分析。這裡的理論基礎就是每一個節點都是條件,在上一個輸出的前提下算出整個序列的概率。
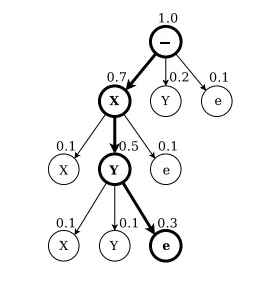
如上圖,字首查詢解碼字母X,Y,在標籤alphabet(x,y)上,每個節點要麼以(“e”)結束,要麼在其父節點上擴充套件字首。擴充套件節點上面的數字是所有以該字首開頭的標籤的總概率。結束節點上方的數字是單個標籤在其父節點結束的概率。在每一次迭代中,都將探索最可能剩餘字首的擴充套件。搜尋結束時,一個標籤(這裡'XY ')比任何剩餘的字首更有可能。
一個訓練的CTC網路的輸出傾向於形成一系列的尖狀物(spikes),尖狀物被預測的blanks分隔開,我們把輸出的序列分為幾部分,這幾個部分可能都是是以一個blank開始和結尾。我們選擇邊界點,這些邊界點的是blank標記的觀察概率超過一個給定的閾值,然後我們對每個部分計算器最可能的標記序列,然後把他們連線起來得到最終的分類。
實踐中,字首搜尋在這個啟發式下工作得很好,通常超過了最佳路徑解碼,但是在有些情況下,效果不佳,例如,當相同的標籤在一個部分邊界的兩側概率都很低時(if the same label is predicted weakly on both sides of a section boundary)。
詳細演算法過程可以看這篇文章:https://blog.csdn.net/zgcr654321/article/details/84872872
CTC網路的訓練:
loss函式是從最大似然估計的規則中衍生出來的,即最小化log似然估計目標序列。給定目標函式,它的導數和網路輸出有關,因此我們可以通過標準的反向傳播計算權重梯度,網路可以通過任何基於梯度優化演算法進行訓練。
loss函式:
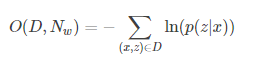
CTC的forward-backward演算法:
前向傳播:
CTC的前向傳播就是要去計算每一個標記的條件概率![]() (
(![]() 代表給定輸入x,輸出為序列L的概率。)。由於一個序列L通常可以有多條路徑經過對映後得到,而隨著序列L長度的增加,相對應的路徑的數目是成指數增加的,因此我們需要一種高效的演算法來計算它。
代表給定輸入x,輸出為序列L的概率。)。由於一個序列L通常可以有多條路徑經過對映後得到,而隨著序列L長度的增加,相對應的路徑的數目是成指數增加的,因此我們需要一種高效的演算法來計算它。
這個問題可以用動態規劃演算法(dynamic programming algorithm)解決,類似於HMMs的前向後向演算法,核心思想是對一個標記的所有路徑求和可以被分解為一個迭代路徑的求和,路徑對應標記的字首,這個迭代過程可以用遞迴的前向和後向變數高效的計算。
對於一個長度為r的序列q,用![]() 表示開始的p個符號,
表示開始的p個符號,![]() 表示最後的p個符號。然後對於一個標記L,定義前向變數
表示最後的p個符號。然後對於一個標記L,定義前向變數![]() ,表示在時刻t,
,表示在時刻t,![]() 的概率和。
的概率和。
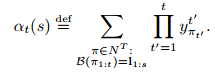
![]() 可以遞迴地用αt-1(s)和αt-1(s-1)進行遞迴計算。
可以遞迴地用αt-1(s)和αt-1(s-1)進行遞迴計算。
考慮到輸出路徑中還有空白(blanks),我們在每一對標籤之間插入了空白,在開始和末尾也加入了空白,這樣我們用L‘表示這個新的標記,L’的長度就為2|l|+1(比如序列L是五個字母,在每個字母前後插上一個空白,L'的長度就是11)。
在計算l’字首的概率中,我們允許空白和非空白標籤之間轉移,我們允許所有的字首要麼以一個空白(b)開始,要麼是l的第一個標籤![]() 開始。
開始。

加入![]() 這個條件是因為這些變數對應的狀態沒有留下足夠的時間步去完成這個序列,如下圖右上角中未連線的圓圈:
這個條件是因為這些變數對應的狀態沒有留下足夠的時間步去完成這個序列,如下圖右上角中未連線的圓圈:
這裡的例子是輸入資料的對應標籤為CAT,每個字母前後都加了blank。

圖中黑圈代表標籤(labels),白圈代表空白。箭頭代表允許的轉移。前向變數往箭頭方向進行更新,後向變數往箭頭的反方向更新。
L的概率是L'所有概率的求和,並且去除了T時刻的最後的blank得到的。
![]()
假設T=3,s=4:

這裡尾部元素為A,並且把除尾部以外所有的blank都去掉得到的sequence是CA,注意這裡的概率是尾部不為blank的 的概率。
假設T=3,s=5:

這裡尾部元素為blank,並且把除尾部以外所有的blank都去掉得到的sequence是CA,注意這裡的概率是尾部為blank的 的概率。
反向傳播:
反向變數![]() 是t時刻
是t時刻![]() 的概率和。
的概率和。

實際上,上面的遞迴將會迅速導致任何電腦的下溢,因此,我們需要變換一下。用α^代替α,用β^代替β:
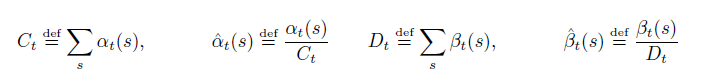
為了評估最大似然誤差,我們需要用到自然對數。
極大似然估計的訓練:
訓練的目標是同時最大化訓練集上所有正確分類的log概率,即優化下式:
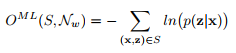
這個就是損失函式。可以寫成下面的形式:
![]()
![]() 代表給定輸入x,輸出序列z的概率,S為訓練集。
代表給定輸入x,輸出序列z的概率,S為訓練集。
損失函式可以解釋為:給定樣本x後輸出正確label的概率的乘積,再取負對數就是損失函數了。取負號之後我們通過最小化損失函式,就可以使輸出正確的label的概率達到最大了。
為了用梯度下降訓練網路,我們需要就對損失函式進行微分,得到下式:
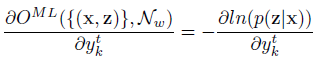
上式可以用前向變數與反向變數計算。
主要思想是:對於一個標記L,在給定s和t的情況下,前向和後向變數的內積(這裡內積其實就是![]() 相乘)就是對應的L所有可能路徑的概率。
相乘)就是對應的L所有可能路徑的概率。
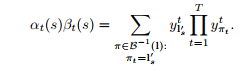
又
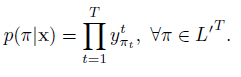
故可得:
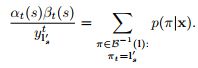
又
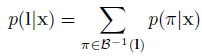
由於這些路徑經過了時刻t的![]() ,對於任意時刻t,我們可以求得:
,對於任意時刻t,我們可以求得:
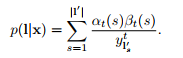
由於網路的輸出是條件獨立的,我們需要考慮在時刻t經過標記k的那些路徑,得到p(L|x)的偏導數,這是對於![]() 而言的。相同的標籤可能會重複幾次在一個標記L中,我們定義了一個標籤k出現的位置集合,記為
而言的。相同的標籤可能會重複幾次在一個標記L中,我們定義了一個標籤k出現的位置集合,記為![]() 。它可能是空的。我們然後去求微分:
。它可能是空的。我們然後去求微分: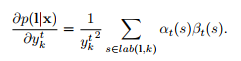
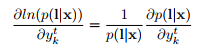
當L=z時,我們可以利用前面的公式
![]() 和
和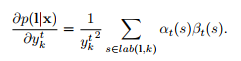 推匯出下式:
推匯出下式:
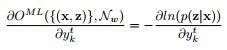
最後,對於softmax層的反向傳播的梯度,我們需要目標函式對未歸一化的輸出![]() 求偏導:
求偏導:
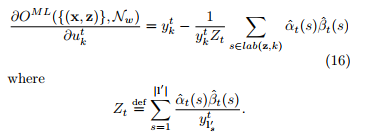
上式就是網路訓練期間的誤差訊號“errorsignal”,如下圖:

這是訓練期間對CTC誤差訊號的評估,左邊的一列是訓練不同階段同一個序列的輸出啟用(虛線是blank單元),右邊一列與之對應的是誤差訊號,誤差在水平軸上的增加了與之對應的輸出啟用,在水平軸下面的代表減少了與之對應的輸出啟用。
一開始網路有少量的隨機權重,誤差僅由目標序列決定。隨後網路開始做預測,錯誤開始呈現區域性化。最後網路強烈的預測正確的標籤,錯誤幾乎消失了。
CTC Loss的侷限性:
CTC loss在計算時假設每個label相互獨立,在這樣的假設下概率才可以相乘來計算條件概率。但是實際上,每個label之間的概率不是相互獨立的。 比如說語言中, the bird is fly in the sky. 最後一個單詞根據上下文很容易猜到是sky。 這個問題可以通過beam search , language modeling來解決。當然這個也未必是壞事, 比如希望模型能識別多個語言, 那language modelling可能就不需要了。
CTC的應用:
神經網路+CTC的結構除了可以應用到語音識別的聲學模型訓練上以外,也可以用到任何一個輸入序列到一個輸出序列的訓練上(要求:輸入序列的長度大於輸出序列)。
比如,OCR識別也可以採用RNN+CTC的模型來做,將包含文字的圖片每一列的資料作為一個序列輸入給RNN+CTC模型,輸出是對應的漢字,因為要好多列才組成一個漢字,所以輸入的序列的長度遠大於輸出序列的長度。而且這種實現方式的OCR識別,也不需要事先準確的檢測到文字的位置,只要這個序列中包含這些文字就好了。
CTC計算舉例:
假設訓練集為![]() 表示有N個訓練樣本,x是輸入樣本,z是對應的真實label。一個樣本的輸入是一個序列,輸出的label也是一個序列,輸入的序列長度大於輸出的序列長度。
表示有N個訓練樣本,x是輸入樣本,z是對應的真實label。一個樣本的輸入是一個序列,輸出的label也是一個序列,輸入的序列長度大於輸出的序列長度。
對於其中一個樣本![]() ,
,![]() 表示一個長度為T幀的資料,每一幀的資料是一個維度為m的向量,即每個
表示一個長度為T幀的資料,每一幀的資料是一個維度為m的向量,即每個![]() 。 xi可以理解為對於一段語音,每25ms作為一幀,其中第i幀的資料是經過MFCC計算後得到的結果。
。 xi可以理解為對於一段語音,每25ms作為一幀,其中第i幀的資料是經過MFCC計算後得到的結果。
![]() 表示這段樣本語音對應的正確的音素。比如,一段發音“你好”的聲音,經過MFCC計算後,得到特徵x, 它的文字資訊是“你好”,對應的音素資訊是z=[n,i,h,a,o]z=[n,i,h,a,o](這裡暫且將每個拼音的字母當做一個音素)。
表示這段樣本語音對應的正確的音素。比如,一段發音“你好”的聲音,經過MFCC計算後,得到特徵x, 它的文字資訊是“你好”,對應的音素資訊是z=[n,i,h,a,o]z=[n,i,h,a,o](這裡暫且將每個拼音的字母當做一個音素)。
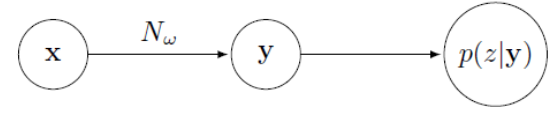
特徵x在經過RNN的計算之後,在經過一個softmax層,得到音素的後驗概率y。![]() 表示在t時刻,發音為音素k的概率,其中音素的種類個數一共n個, k表示第k個音素,在一幀的資料上所有的音素概率加起來為1。即:
表示在t時刻,發音為音素k的概率,其中音素的種類個數一共n個, k表示第k個音素,在一幀的資料上所有的音素概率加起來為1。即:
![]()
這個過程可以看做是對輸入的特徵資料x做了變換![]() ,其中
,其中![]() 表示RNN的變換,w表示RNN中的引數集合。
表示RNN的變換,w表示RNN中的引數集合。
過程如下圖:

以一段“你好”的語音為例,經過MFCC特徵提取後產生了30幀,每幀含有12個特徵,即![]() (這裡以14個音素為例,實際上音素有200個左右),矩陣裡的每一列之和為1。後面的基於CTC-loss的訓練就是基於後驗概率y計算得到的。
(這裡以14個音素為例,實際上音素有200個左右),矩陣裡的每一列之和為1。後面的基於CTC-loss的訓練就是基於後驗概率y計算得到的。
路徑π和B變換:
在實際訓練中我們並不知道每一幀對應的音素,因此進行訓練比較困難。我們可以先考慮一種簡單的情況,已知每一幀的音素的標籤z′, 即訓練樣本為x和z′,其中z′不再是簡單的[n,i,h,a,o][n,i,h,a,o]標籤,而是:
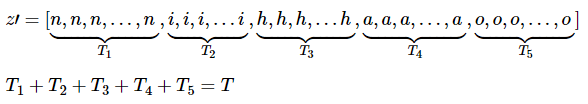
在我們的例子中:
![]()
z′包含了每一幀的標籤。
在這種情況下有:
![]()
該值即為後驗概率圖中用黑線圈起來的部分相乘。我們希望相乘的值越大越好,因此,數學規劃可以寫為:
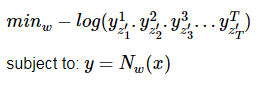
目標函式對於後驗概率矩陣y中的每個元素![]() 的偏導數為:
的偏導數為:
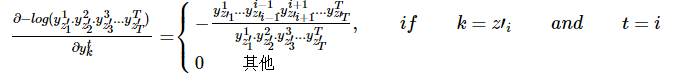
也就是說,在每個時刻t(對應矩陣的一列),目標只與![]() 是相關的,在這個例子中是與被框起來的元素相關。
是相關的,在這個例子中是與被框起來的元素相關。
其中![]() 可以看做是RNN模型,如果訓練資料的每一幀都標記了正確的音素,那麼訓練過程就很簡單了,但實際上這樣的標記過的資料非常稀少,而沒有逐幀標記的資料很多,CTC可以做到用未逐幀標記的資料做訓練。
可以看做是RNN模型,如果訓練資料的每一幀都標記了正確的音素,那麼訓練過程就很簡單了,但實際上這樣的標記過的資料非常稀少,而沒有逐幀標記的資料很多,CTC可以做到用未逐幀標記的資料做訓練。
首先定義幾個符號:
![]()
表示所有音素的集合
![]()
表示一條由L中元素組成的長度為T的路徑,比如z′就是一條路徑,以下為幾個路徑的例子:
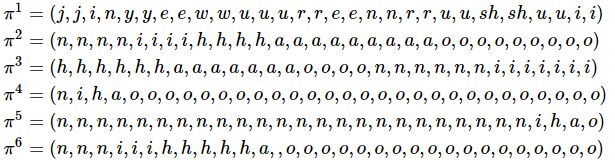
這6條路徑中,π1可以被認為是“今夜無人入睡”, π2可以被認為是在說“你好”,π3可以被認為是在說“好你”,π4,π5,π6都可以認為是在說“你好”。
定義B變換,表示簡單的壓縮,例如:
![]()
以上面6條路徑為例:
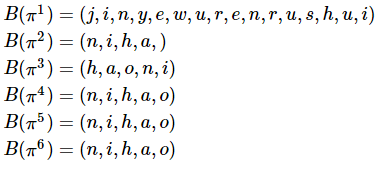
因此,如果有一條路徑π有![]() ,則可以認為π是在說“你好”。即使它是如π4所示,有很多“o”的音素,而其他音素很少。路徑
,則可以認為π是在說“你好”。即使它是如π4所示,有很多“o”的音素,而其他音素很少。路徑![]() 的概率為它所經過的矩陣y上的元素相乘:
的概率為它所經過的矩陣y上的元素相乘:
![]()
因此在沒有對齊的情況下,目標函式應該為![]() 中所有元素概率之和。 即:
中所有元素概率之和。 即:
![]()
如在T=30,音素為[n,i,h,a,o]的情況下,共有![]() 條路徑可以被壓縮為[n,i,h,a,o]。路徑數目的計算公式為
條路徑可以被壓縮為[n,i,h,a,o]。路徑數目的計算公式為![]() ,量級大約為
,量級大約為![]() 。一段30秒包含50個漢字的語音,其可能的路徑數目可以高達10的8次方,顯然這麼大的路徑數目是無法直接計算的。因此CTC方法中借用了HMM中的向前向後演算法來計算。
。一段30秒包含50個漢字的語音,其可能的路徑數目可以高達10的8次方,顯然這麼大的路徑數目是無法直接計算的。因此CTC方法中借用了HMM中的向前向後演算法來計算。
訓練實施方法:
CTC的訓練過程是通過![]() 調整w的值使得4中的目標值最大,計算的過程如下:
調整w的值使得4中的目標值最大,計算的過程如下:
因此,只要得到![]() ,即可根據反向傳播,得到,即可根據反向傳播,得到
,即可根據反向傳播,得到,即可根據反向傳播,得到![]() 。下面以“你好”為例,介紹該值的計算方法。
。下面以“你好”為例,介紹該值的計算方法。
首先,根據前面的例子,找到所有可能被壓縮為z=[n,i,h,a,o]的路徑,記為![]() 。 可知所有π均有
。 可知所有π均有![]() 的形式,即目標函式只與後驗概率矩陣y中表示n,i,h,a,o的5行相關,因此為了簡便,我們將這5行提取出來,如下圖所示
的形式,即目標函式只與後驗概率矩陣y中表示n,i,h,a,o的5行相關,因此為了簡便,我們將這5行提取出來,如下圖所示
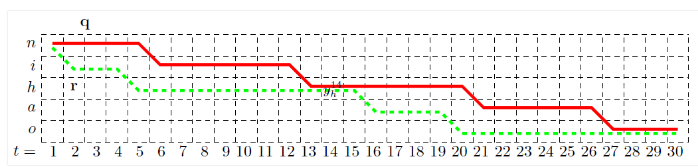
在每一個點上,路徑只能向右或者向下轉移,畫出兩條路徑,分別用q和r表示,這兩條路徑都經過![]() 這個點,表示這兩點路徑均在第14幀的時候在發“h”音。因為在目標函式4的連加項中,有的項與
這個點,表示這兩點路徑均在第14幀的時候在發“h”音。因為在目標函式4的連加項中,有的項與![]() 無關,因此可以剔除這一部分,只留下與
無關,因此可以剔除這一部分,只留下與![]() 有關的部分,記為
有關的部分,記為![]()

這裡的q和r就是與![]() 相關的兩條路徑。用
相關的兩條路徑。用![]() 和
和![]() 分別表示q在
分別表示q在![]() 之前和之後的部分,同樣的,用
之前和之後的部分,同樣的,用![]() 和
和![]() 分別表示r在
分別表示r在![]() 之前和之後的部分.。可以發現,
之前和之後的部分.。可以發現,![]() 與
與![]() 同樣也是兩條可行的路徑。
同樣也是兩條可行的路徑。
![]() 、
、![]() 、q、r這四條路徑的概率之和為:
、q、r這四條路徑的概率之和為:

可以發現,該值可以總結為:(前置項)![]() (後置項)。由此,對於所有的經過
(後置項)。由此,對於所有的經過![]() 的路徑,有:
的路徑,有:
![]()
定義:
![]()
該值可以理解為從初始到![]() 這一段裡,所有正向路徑的概率之和。並且發現,
這一段裡,所有正向路徑的概率之和。並且發現,![]() 可以由
可以由![]() 和
和![]() 遞推得到,即:
遞推得到,即:
![]()
該遞推公式的含義是,只有在t=13時發音是“h”或“i”,在t=14時才有可能發音是“h”。那麼在t=14時刻發音是“h”的所有正向路徑概率![]() 就等於在t=13時刻,發音為“h”的正向概率
就等於在t=13時刻,發音為“h”的正向概率![]() 加上發音為“i”的正向概率
加上發音為“i”的正向概率![]() ,再乘以當前音素被判斷為“h”的概率
,再乘以當前音素被判斷為“h”的概率![]() 。由此可知,每個
。由此可知,每個![]() 都可以由
都可以由![]() 和
和![]() 兩個值得到。α的遞推流程如下圖所示:
兩個值得到。α的遞推流程如下圖所示:

即每個值都由上一個時刻的一個或者兩個值得到,總計算量大約為2.T.音素個數。類似的,定義![]() , 遞推公式為:
, 遞推公式為:
![]()
因此有:
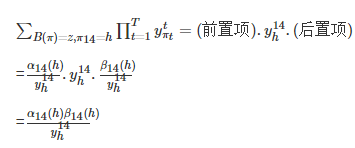
然後:
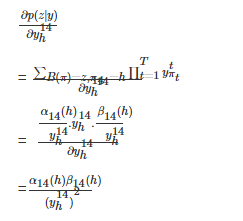
得到此值後,就可以根據反向傳播演算法進行訓練了。
可以看到,這裡總的計算量非常小,計算α和β的計算量均大約為(2.T.音素個數),(加法乘法各一次),得到α和β之後,在計算對每個![]() 的偏導值的計算量為(3.T.音素個數),因此總計算量大約為(7.T.音素個數),這個計算量很小。因此這個演算法在計算量上很有優勢。
的偏導值的計算量為(3.T.音素個數),因此總計算量大約為(7.T.音素個數),這個計算量很小。因此這個演算法在計算量上很有優勢。

