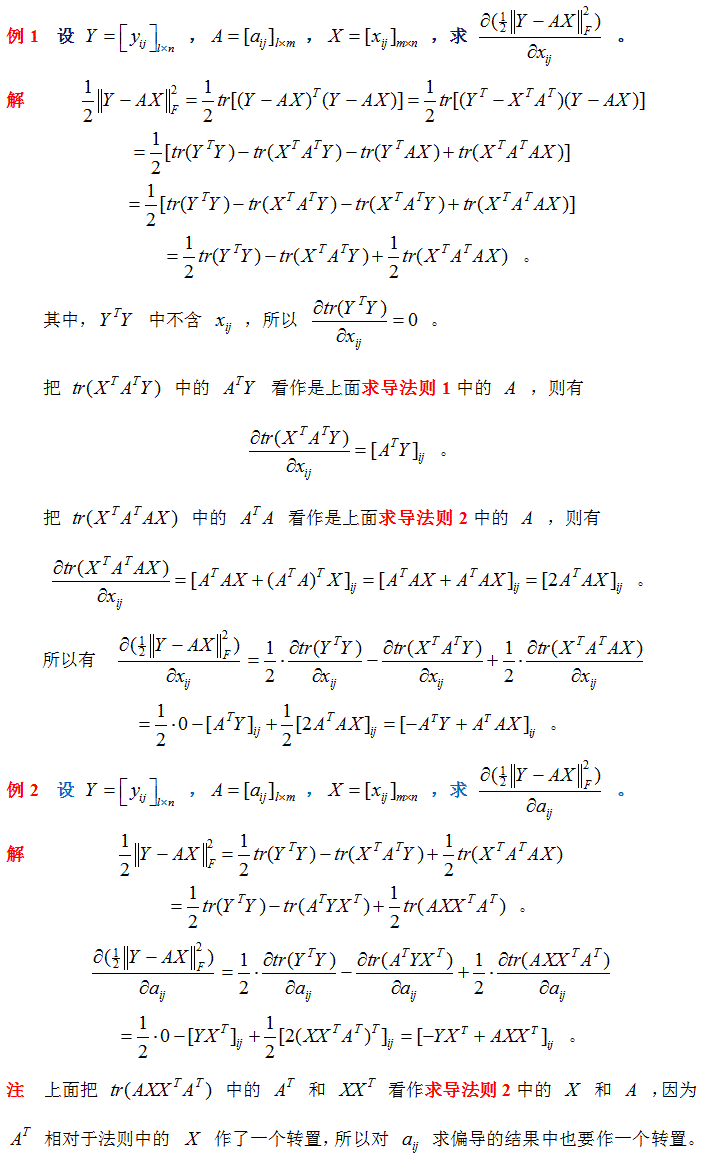矩陣的 Frobenius 範數及其求偏導法則
阿新 • • 發佈:2018-12-10
原文:https://blog.csdn.net/txwh0820/article/details/46392293
矩陣的跡求導法則

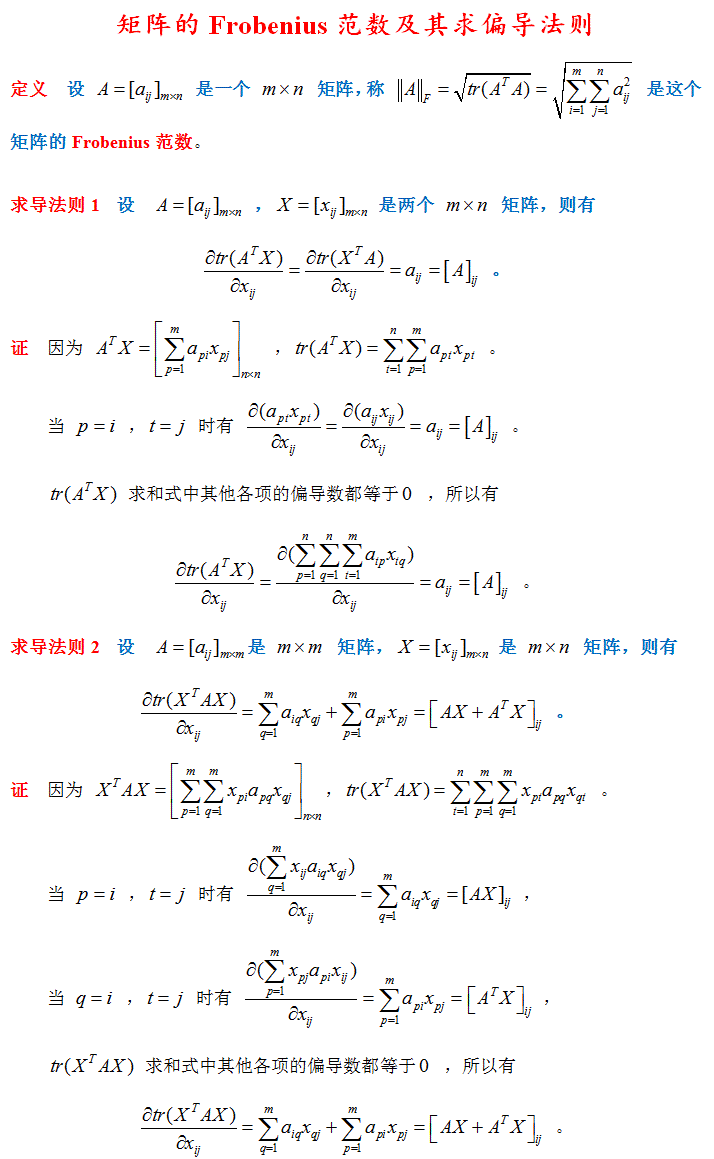
1. 複雜矩陣問題求導方法:可以從小到大,從scalar到vector再到matrix
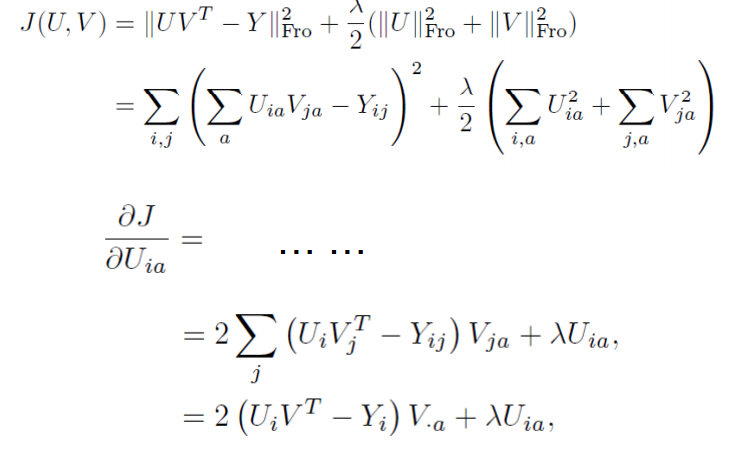
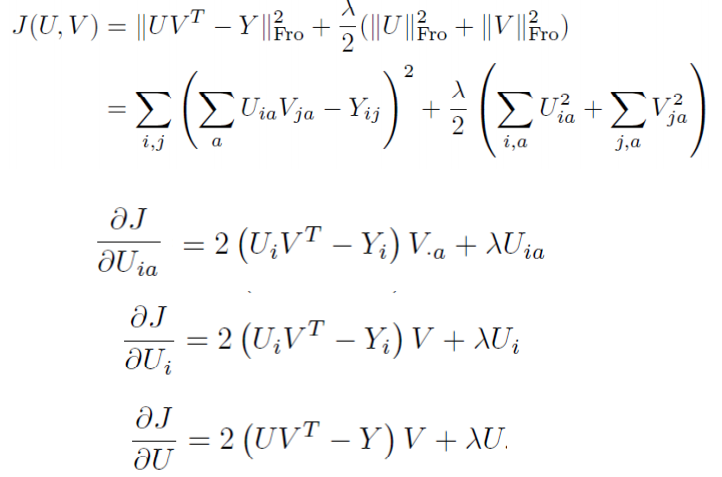
2. x is a column vector, A is a matrix
d(A∗x)/dx=Ad(A∗x)/dx=A
3. Practice:
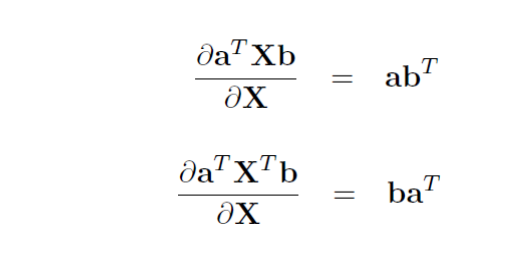
4. 矩陣求導計演算法則
求導公式(撇號為轉置):
Y = A * X –> DY/DX = A’
Y = X * A –> DY/DX = A
Y = A’ * X * B –> DY/DX = A * B’
Y = A’ * X’ * B –> DY/DX = B * A’
乘積的導數:
d(f*g)/dx=(df’/dx)g+(dg/dx)f’
一些結論:
- 矩陣Y對標量x求導:
相當於每個元素求導數後轉置一下,注意M×N矩陣求導後變成N×M了
Y = [y(ij)]–> dY/dx = [dy(ji)/dx] - 標量y對列向量X求導:
注意與上面不同,這次括號內是求偏導,不轉置,對N×1向量求導後還是N×1向量
y = f(x1,x2,..,xn) –> dy/dX= (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)’ - 行向量Y’對列向量X求導:
注意1×M向量對N×1向量求導後是N×M矩陣。
將Y的每一列對X求偏導,將各列構成一個矩陣。
重要結論:
dX’/dX =I
d(AX)’/dX =A’ - 列向量Y對行向量X’求導:
轉化為行向量Y’對列向量X的導數,然後轉置。
注意M×1向量對1×N向量求導結果為M×N矩陣。
dY/dX’ =(dY’/dX)’ - 向量積對列向量X求導運演算法則:
注意與標量求導有點不同。
d(UV’)/dX =(dU/dX)V’ + U(dV’/dX)
d(U’V)/dX =(dU’/dX)V + (dV’/dX)U’
重要結論:
d(X’A)/dX =(dX’/dX)A + (dA/dX)X’ = IA + 0X’ = A
d(AX)/dX’ =(d(X’A’)/dX)’ = (A’)’ = A
d(X’AX)/dX =(dX’/dX)AX + (d(AX)’/dX)X = AX + A’X - 矩陣Y對列向量X求導:
將Y對X的每一個分量求偏導,構成一個超向量。
注意該向量的每一個元素都是一個矩陣。 - 矩陣積對列向量求導法則:
d(uV)/dX =(du/dX)V + u(dV/dX)
d(UV)/dX =(dU/dX)V + U(dV/dX)
重要結論:
d(X’A)/dX =(dX’/dX)A + X’(dA/dX) = IA + X’0 = A - 標量y對矩陣X的導數:
類似標量y對列向量X的導數,
把y對每個X的元素求偏導,不用轉置。
dy/dX = [Dy/Dx(ij) ]
重要結論:
y = U’XV= ΣΣu(i)x(ij)v(j) 於是 dy/dX = [u(i)v(j)] =UV’
y = U’X’XU 則dy/dX = 2XUU’
y =(XU-V)’(XU-V) 則 dy/dX = d(U’X’XU - 2V’XU + V’V)/dX = 2XUU’ - 2VU’ +0 = 2(XU-V)U’ - 矩陣Y對矩陣X的導數:
將Y的每個元素對X求導,然後排在一起形成超級矩陣。
10.乘積的導數
d(f*g)/dx=(df’/dx)g+(dg/dx)f’
結論
d(x’Ax)=(d(x”)/dx)Ax+(d(Ax)/dx)(x”)=Ax+A’x (注意:”是表示兩次轉置)
矩陣求導 屬於 矩陣計算,應該查詢 Matrix Calculus 的文獻:
http://www.psi.toronto.edu/matrix/intro.html#Intro
http://www.psi.toronto.edu/matrix/calculus.html
http://www.stanford.edu/~dattorro/matrixcalc.pdf
http://www.colorado.edu/engineering/CAS/courses.d/IFEM.d/IFEM.AppD.d/IFEM.AppD.pdf
http://www4.ncsu.edu/~pfackler/MatCalc.pdf
http://center.uvt.nl/staff/magnus/wip12.pdf