1. 問題描述

跨語言詞向量解決什麼問題呢？當我們有英文標註資料，在英文資料上訓練好模型，但是我們沒有中文標註資料去訓練模型，怎麼辦？跨語言詞向量就是將英文詞向量和中文詞向量對映到一個空間裡，這樣相當於中英文資料都只是整體資料的一部分，我拿整體資料中的一部分（即英文資料）做訓練，拿整體資料中的另一部分（即中文資料）做測試，所以就不需要重新訓練模型，解決了中文標註資料缺失的問題。啊說的有點多了，西湖的水我的淚。

對於跨語言詞向量的文獻，我看了兩篇，一篇是16年EMNLP的《Learning principled bilingual mappings of word embeddings while preserving monolingual invariance》，用的是有監督的方法，另一篇是18年ACL的《A robust self-learning method for fully unsupervised cross-lingual mappings of word embeddings》，用的是無監督的方法。這篇部落格介紹有監督的那一篇。

這篇文章主要是對之前的有監督方法訓練跨語言詞向量的文獻做了一個總結，提出了一個通用框架，融合了之前一些演算法的本質，我認為如果只是做個調研的話，看了這一篇之後，基本可以不用看之前的那些有監督的文獻了。

2. 演算法

和分別表示兩類語言中獨立訓練好的詞嵌入矩陣，需要自己先訓練好，或者拿別人現成的。其中每行代表一個詞的詞向量，每一列代表詞向量的第幾維。的第行和的第行對應的是一個詞義，比如‘你好’和‘hello’。我們需要求一個轉換矩陣以使近似於，即

等價於求Frobenius 範數：

所以是的最小二乘解，可以用Moore-Penrose廣義逆求解，，，可以用SVD求解。

3. 必要的trick

上述已經可以求出了，但還是要加一些必要的trick，為了有更好的效果。

3.1. 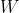矩陣必須是正交矩陣以保證單語原來的方差

首先為了保證轉換後的單語方差，和以前的單語方差一樣，即，必須使，這樣可以避免詞向量在單語任務上效能下降。

若，那的解可以表示成，其中和是對奇異值分解得來的，即。

證明如下：

代表了主對角元素的和，第二行變成第三行是因為，與無關。第四行變成第五行是因為。

若，，因為都是正交矩陣，所以是正交矩陣，因為是對角矩陣，所以對角保持不變對角線的和才為最大，則，則。

但是我在這裡有個疑問，如果有朋友知道請教教我～對角保持不變對角線的和才為最大感覺應該是建立在矩陣正定的基礎呢，那麼矩陣正定嗎。

3.2對每個單詞的詞向量做normalization可以將問題轉化為餘弦相似度

這裡的normalization指的是將變為

而且又因為是正交矩陣，那麼目標函式就變成了

3.3對詞向量的每一列去均值可以將問題轉化為求最大協方差

對詞向量的每一列去均值，相當於對資料空間的每一維去均值，讓資料均勻得分佈在多維空間原點附近，為什麼要這樣做呢。拿二維空間舉個例子，看下我自己畫的圖。

如圖所示，假設點A和點B是資料空間裡兩個差別比較大的點，只是恰巧他們都在第一象限中，這樣求出餘弦相似度會說明他們很相似，但如果對每一維去均值之後，他們會分別分佈在第一象限和第三象限中，這樣求出餘弦相似度會說明他們差別很大，更能反映出資料本來的特徵。

這裡文章中拿CCA來對比，由於時間原因先不寫了，過段時間一定加上。

4. 實驗

實驗部分還沒細看，過幾天一定加上。