CART迴歸樹演算法過程
CART決策樹演算法是一種分類及迴歸樹演算法,既可以用於分類,也可以用於迴歸。但是在李航老師的《統計學習方法》一書中,並沒有詳細介紹迴歸樹,更多的是介紹分類樹,所以有必要對CART迴歸樹進行簡單介紹,有利於對CART樹用於迴歸的操作,因為後續GBDT演算法也是在CART迴歸樹的基礎上進行的,所以深入理解CART迴歸樹非常重要。
迴歸樹:使用平方誤差最小準則
訓練集為:D={(x1,y1), (x2,y2), …, (xn,yn)}。
輸出Y為連續變數,將輸入劃分為M個區域,分別為R1,R2,…,RM,每個區域的輸出值分別為:c1,c2,…,cm則迴歸樹模型可表示為:
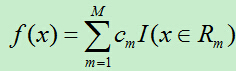
則平方誤差為:
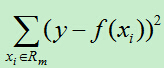
假如使用特徵j的取值s來將輸入空間劃分為兩個區域,分別為:

我們需要最小化損失函式,即:
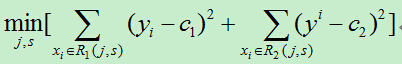
其中c1,c2分別為R1,R2區間內的輸出平均值。(此處與統計學習課本上的公式有所不同,在課本中裡面的c1,c2都需要取最小值,但是,在確定的區間中,當c1,c2取區間輸出值的平均值時其平方會達到最小,為簡單起見,故而在此直接使用區間的輸出均值。)
為了使平方誤差最小,我們需要依次對每個特徵的每個取值進行遍歷,計算出當前每一個可能的切分點的誤差,最後選擇切分誤差最小的點將輸入空間切分為兩個部分,然後遞迴上述步驟,直到切分結束。此方法切分的樹稱為最小二乘迴歸樹。
最小二乘迴歸樹生成演算法:
1)依次遍歷每個特徵j,以及該特徵的每個取值s,計算每個切分點(j,s)的損失函式,選擇損失函式最小的切分點。
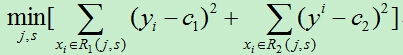
2)使用上步得到的切分點將當前的輸入空間劃分為兩個部分
3)然後將被劃分後的兩個部分再次計算切分點,依次類推,直到不能繼續劃分。
4)最後將輸入空間劃分為M個區域R1,R2,…,RM,生成的決策樹為:
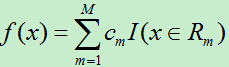
其中cm為所在區域的輸出值的平均。
總結:此方法的複雜度較高,尤其在每次尋找切分點時,需要遍歷當前所有特徵的所有可能取值,假如總共有F個特徵,每個特徵有N個取值,生成的決策樹有S個內部節點,則該演算法的時間複雜度為:O(F*N*S)。
