深度學習不深度-PCA與AutoEncoder
1.AutoEncoder
AutoEncoder稱之為自編碼器,自編碼器過程如下:
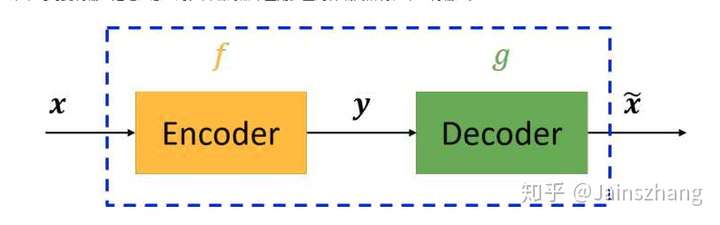
我們的目標是使得 越接近越好。x經過Encoder後得到y(code)可以看作是一個降維的過程,因此與PCA類似。AutoEncoder原理十分簡單,可以利用y(code)做分類,在y(code)較少的情況下,則需要考慮加入噪音來平衡。
2. PCA涉及數學知識
PCA是一種資料分析方法,將原始資料變換成一組各維度線性無關的表示,可以用來提取主要特徵,進而實現降維。眾所周知,在機器學習演算法中,演算法的複雜度與資料的維度是緊密相關的,因此提取資料的主要特徵來降低演算法的複雜度是一個不錯的選擇。
相關性:
內積幾何解釋:向量A和向量B,A B=|A|*cos(
)*|B|,也就是A在B上的投影長度
B的模。
基:線上性代數中,基(也稱為基底)是描述、刻畫向量空間的基本工具。向量空間的基是它的一個特殊的子集,基的元素稱為基向量。向量空間中任意一個元素,都可以唯一地表示成基向量的線性組合。如果基中元素個數有限,就稱向量空間為有限維向量空間,將元素的個數稱作向量空間的維數-----來自百度百科。說來說去,基就類似於一個單位,某一個向量可以表示為基向量的線性組合,基向量的維度決定了變換後向量的維度,因此在降維中可以選擇維度較小的基。
問題在於:在PCA降維過程中如何合理的選擇基呢?(先留著,最後回答)
具體問題:在儘量保持原有二維資料的資訊的基礎上,如何用一維資料來表示二維資料呢?
採用的方法是:選取一條直線,把所有二維上的點投影到該直線上,計算出新的座標,最合理的直線選擇就是希望投影后的投影值儘可能的分散,這樣對原有資料影響最小。
方差:在數學上有一個術語可以用來衡量資料的分散程度,那就是方差。
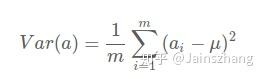
如果把資料a中所有欄位都去均值,則方差就如下:
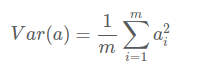
此時降維問題就可以表示為:尋找一個低維度的基,使得所有資料在新基上表示後,新的座標(值)方差最大。
協方差:對於高維(3維以上),我們希望找到一個方向,使得向量投影后的方差最大,但如果低維有2個以上分量該如何做呢?(如何投影?)此時就不能像在2維降低到一維一樣投影了。在利用新的基變換後的欄位儘可能表示更多的原始資訊,同時希望變換後的欄位(分量)之間無相關性,否則就重複表示了(見相關性
降維優化的目標直觀表達:將一組N維向量降低至K維(K>0,K<N),目標是選擇K個單位(模為1)的正交基,使得原始資料變換到這組基上後,各欄位兩兩間協方差為0,而欄位的方差則儘可能大(在正交的約束下,取最大的K個方差)。
矩陣乘法:在連結中第1,2節有介紹。矩陣乘法可以看作是(行/列)向量的線性組合。
協方差矩陣:上面我們匯出了優化目標,但沒有說怎麼做。所以我們要繼續在數學上研究計算方案。我們看到,最終要達到的目的與欄位內方差及欄位間協方差有密切關係。因此我們希望能將兩者統一表示,仔細觀察發現,兩者均可以表示為內積的形式,而內積又與矩陣相乘密切相關。於是我們來了靈感:假設我們只有a和b兩個欄位,那麼我們將它們按行組成矩陣X:
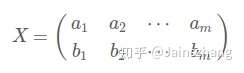
然後讓 ,再乘係數
得到如下:
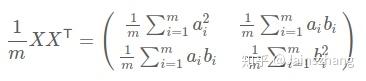
這個矩陣對角線上的兩個元素分別是兩個欄位的方差,而其它元素是a和b的協方差,兩者被統一到了一個矩陣中。
設我們有m個n維資料記錄,將其按列排成n乘m的矩陣X,設C=,則C是一個對稱矩陣,其對角線分別個各個欄位的方差,而第i行j列和j行i列元素相同,表示i和j兩個欄位的協方差。
協方差對角化:根據上述推導,我們發現要達到優化目前,等價於將協方差矩陣對角化:即除對角線外的其它元素化為0,並且在對角線上將元素按大小從上到下排列,這樣我們就達到了優化目的。我們進一步看下原矩陣與基變換後矩陣協方差矩陣的關係:
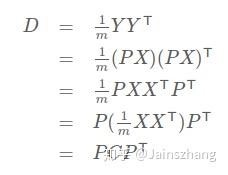
此時優化目標變為:尋找一個矩陣P,滿足是一個對角矩陣,並且對角元素按從大到小依次排列,那麼P的前K行就是要尋找的基,用P的前K行組成的矩陣乘以X就使得X從N維降到了K維並滿足上述優化條件。
由上文知道,協方差矩陣C是一個是對稱矩陣,線上性代數上,實對稱矩陣有一系列非常好的性質:
1)實對稱矩陣不同特徵值對應的特徵向量必然正交。
2)設特徵向量λ重數為r,則必然存在r個線性無關的特徵向量對應於λ,因此可以將這r個特徵向量單位正交化。
由上面兩條可知,一個n行n列的實對稱矩陣一定可以找到n個單位正交特徵向量,設這n個特徵向量為 ,按列組成矩陣:
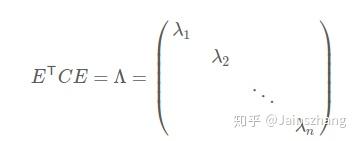
在此處已經找到了矩陣P, 。P是協方差矩陣的特徵向量單位化後按行排列出的矩陣,其中每一行都是C的一個特徵向量。如果設P按照Λ中特徵值的從大到小,將特徵向量從上到下排列,則用P的前K行組成的矩陣乘以原始資料矩陣X,就得到了我們需要的降維後的資料矩陣Y。
介紹完了PCA數學過程,下面給出PCA的演算法過程:
3. PCA演算法過程
總結一下PCA的演算法步驟:
設有m條n維資料。
1)將原始資料按列組成n行m列矩陣X
2)將X的每一行(代表一個屬性欄位)進行零均值化,即減去這一行的均值
3)求出協方差矩陣
4)求出協方差矩陣的特徵值及對應的特徵向量
5)將特徵向量按對應特徵值大小從上到下按行排列成矩陣,取前k行組成矩陣P
6)Y=PX即為降維到k維後的資料
