深度學習:Sigmoid函式與損失函式求導
1、sigmoid函式
sigmoid函式,也就是s型曲線函式,如下:
上面是我們常見的形式,雖然知道這樣的形式,也知道計算流程,不夠感覺並不太直觀,下面來分析一下。
1.1 從指數函式到sigmoid
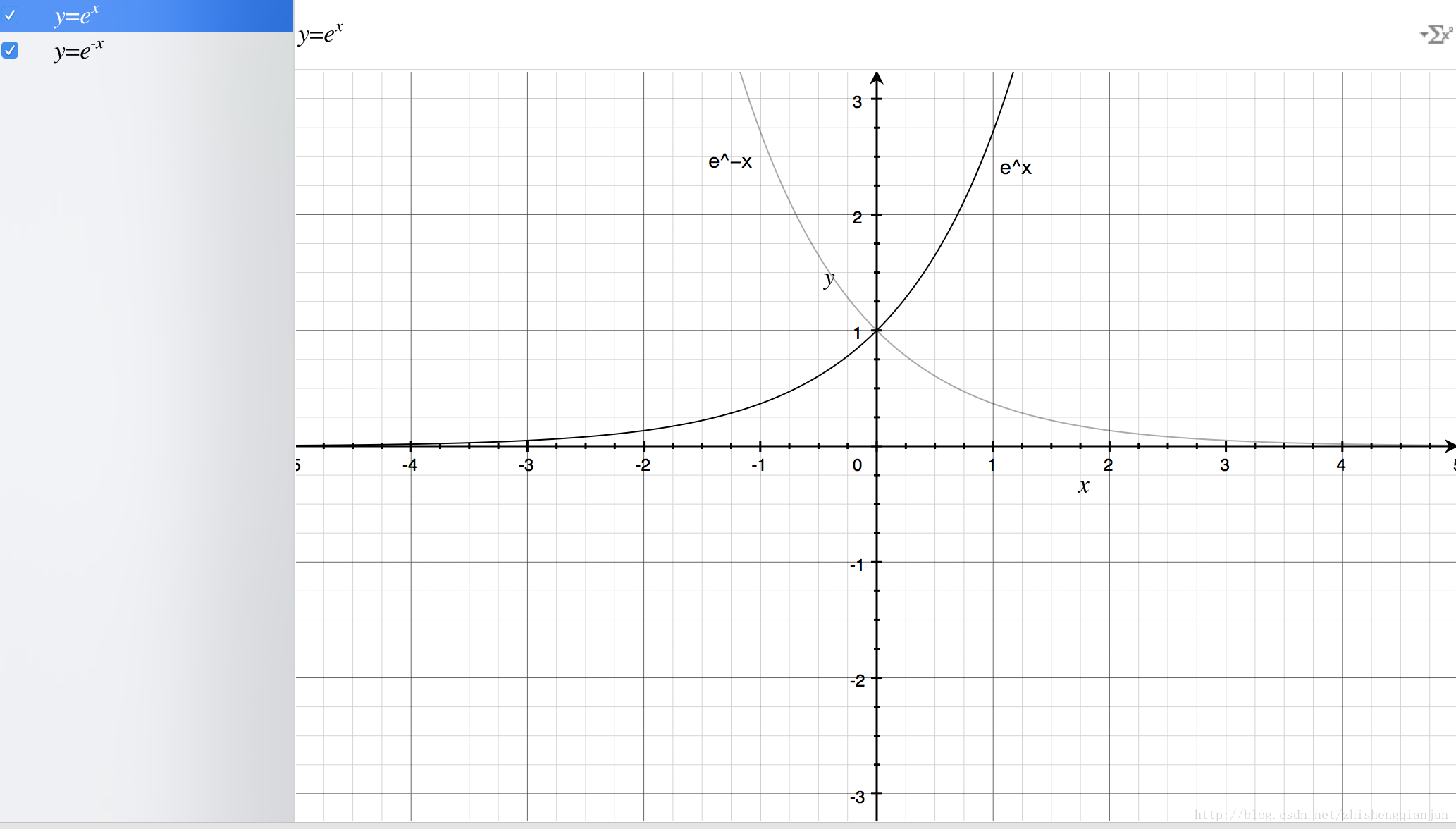
首先我們來畫出指數函式的基本圖形:
從上圖,我們得到了這樣的幾個資訊,指數函式過(0,1)點,單調遞增/遞減,定義域為
如果直接把
1.2 對數函式與sigmoid
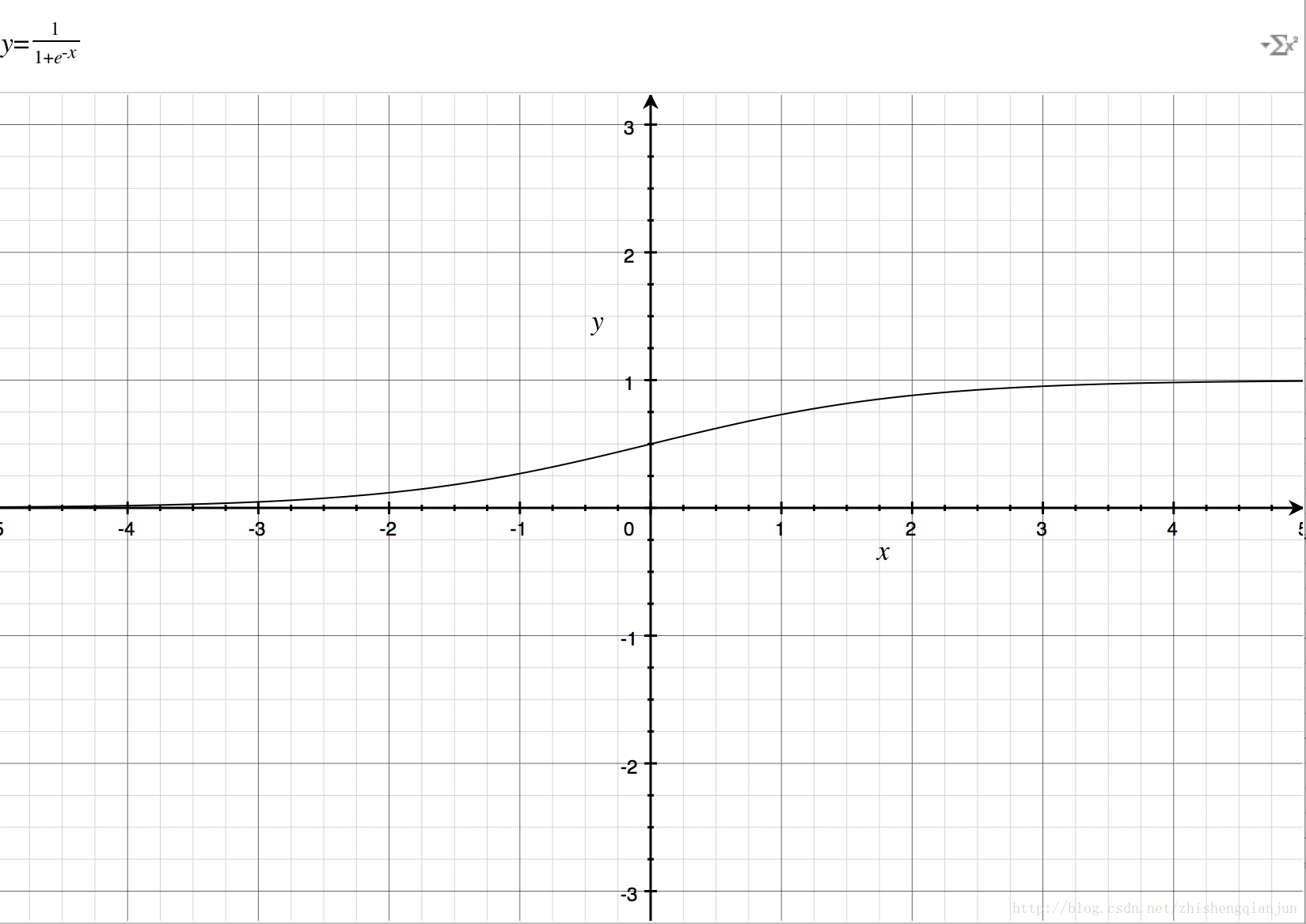
首先來看一下對數函式的影象:
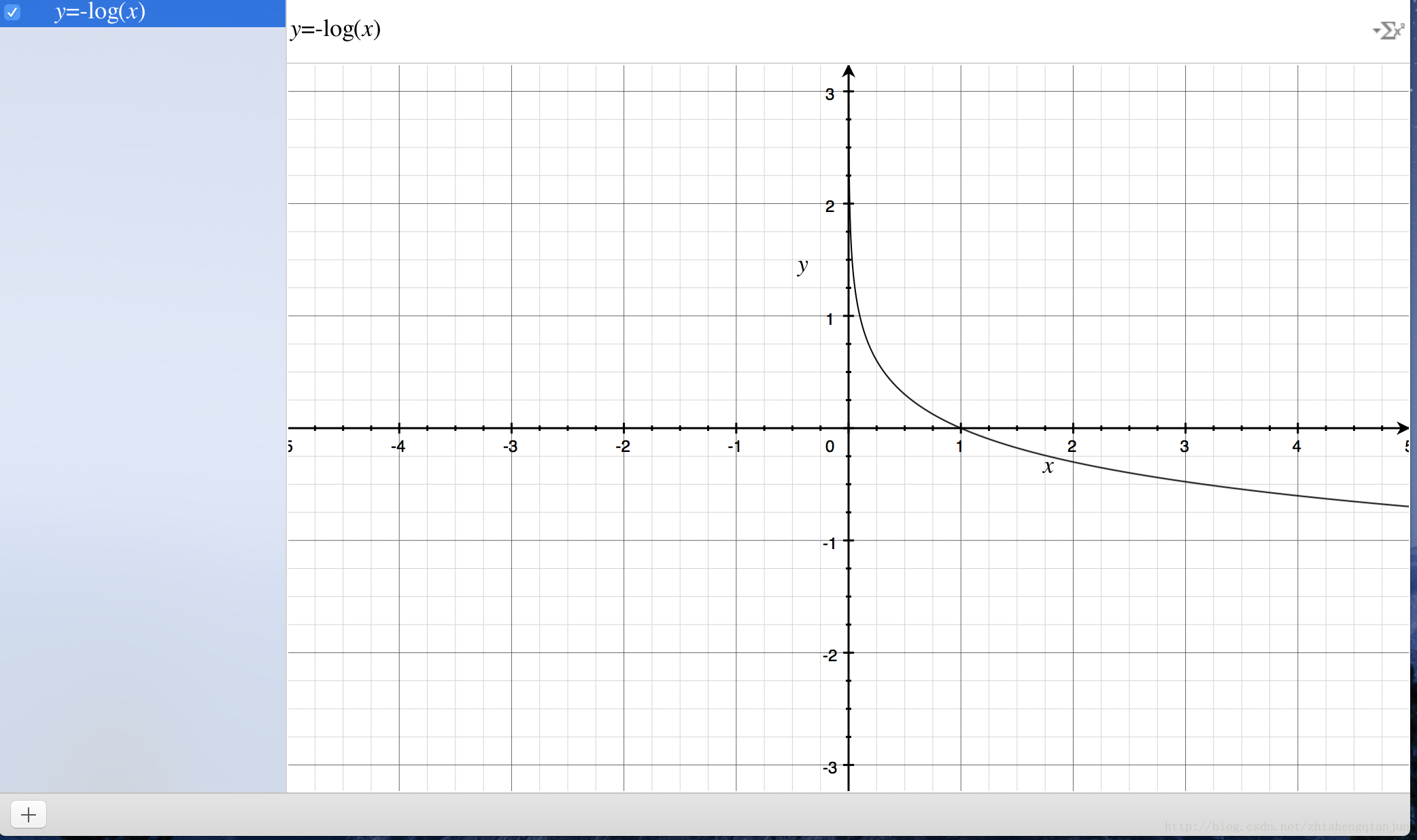
對數函式的影象如上,單調遞減,有一個比較好的特性就是在
我們如何來衡量一個結果與實際計算值得差距呢?一種思路就是,如果結果越接近,差值就越小,反之越大,這個函式就提供了這樣一種思路,如果計算得到的值越接近1,那麼那麼表示與世界結果越接近,反之越遠,所以利用這個函式,可以作為邏輯迴歸分類器的損失函式,如果所有的結果都能接近結果值,那麼就越接近於0,如果所有的樣本計算完成以後,結果接近於0,就表示計算結果與實際結果非常相近。
2、sigmoid函式求導
sigmoid導數具體的推導過程如下:
3、神經網路損失函式求導
神經網路的損失函式可以理解為是一個多級的複合函式,求導使用鏈式法則。
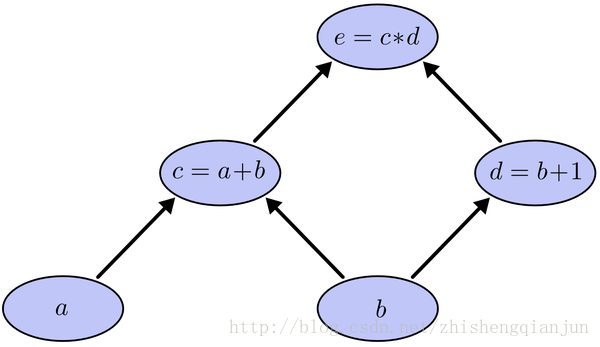
先來說一下常規求導的過程:
這是一個簡單的複合函式,如上圖所示,c是a的函式,e是c的函式,如果我們用鏈式求導法則,分別對a和b求導,那麼就是求出e對c的導數,c對a的導數,乘起來,對b求導則是求出e分別對c和d的導數,分別求c和d對b的導數,然後加起來,這種方法使我們常規的做法,有一個問題就是,我們在求到的過程中,e對c求導計算了2次,如果方程特別複雜,那麼這個計算量就變得很大,怎樣能夠讓每次求導只計算一次呢?
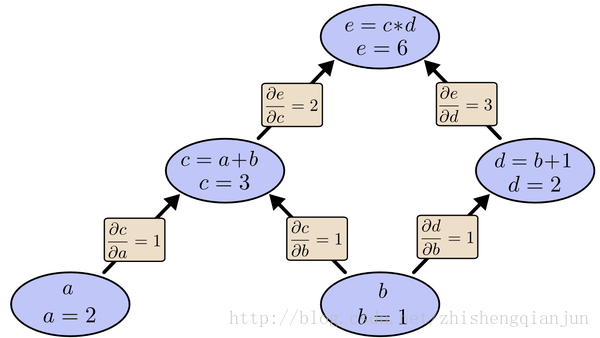
如上圖所示,我們從上往下開始計算,將每個單元的值計算出來,然後計算每個單元的偏導數,儲存下來;
接下來繼續計運算元單元的值,子單元的偏導數,儲存下來;將最後的子單元到根節點所在的路徑的所有偏導乘起來,就是該函式對這個變數的偏導,計算的本質就是從上往下,計算的時候將值存起來,乘到後面的單元上去,這樣每個路徑的偏導計算只需要一次,從上到下計算一遍就得到了所有的偏導數。
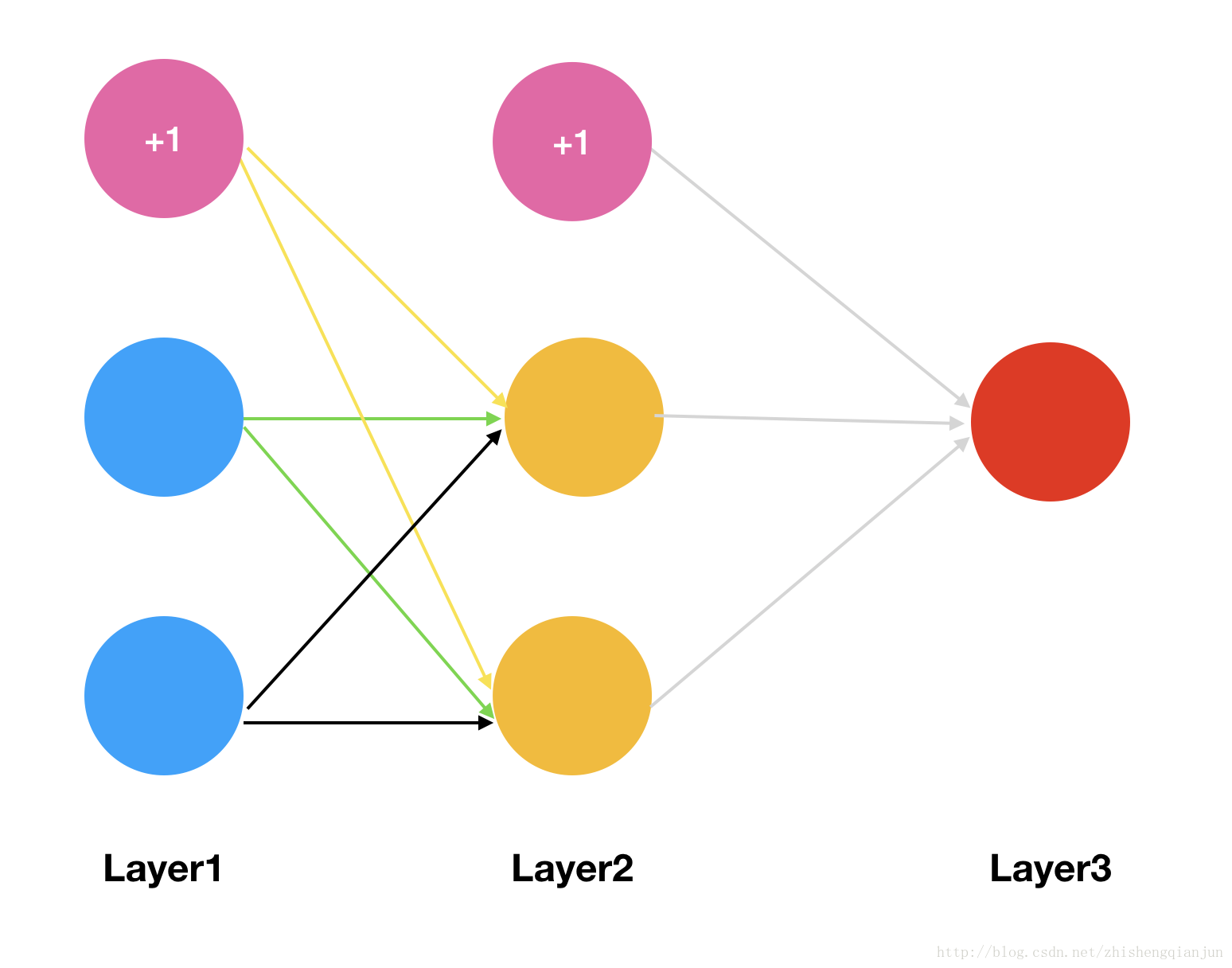
實際上BP(Backpropagation,反向傳播演算法),就是如此計算的,如果現在有一個三層的神經網路,有輸入、一個隱藏層,輸出層,我們對損失函式求權重的偏導數,它是一個複雜的複合函式,如果先對第一層的權重求偏導,然後在對第二層的權重求偏導,會發現,其中有很多重複計算的步驟,就像上面的簡單函式的示例,所以,為了避免這種消耗,我們採用的就是從後往前求偏導,求出每個單元的函式值,求出對應單元的偏導數,儲存下來,一直乘下去,輸入層。
下面用一個簡單的示例來演示一下反向傳播求偏導的過程:
那麼我們會有兩個初始的權重矩陣:
相關推薦
深度學習:Sigmoid函式與損失函式求導
1、sigmoid函式 sigmoid函式,也就是s型曲線函式,如下: 函數:f(z)=11+e−z 導數:f′(z)=f(z)(1−f(z)) 上面是我們常見的形式,雖然知道這樣的形式,也知道計算流程,不夠感覺並不太直觀,下面
在深度學習中Softmax交叉熵損失函式的公式求導
(以下部分基本介紹轉載於點選開啟連結) 在深度學習NN中的output層通常是一個分類輸出,對於多分類問題我們可以採用k-二元分類器來實現,這裡我們介紹softmax。softmax迴歸中,我們解決的是多分類問題(相對於 logistic 迴歸解決的二分類問題),類標
【深度學習原理】交叉熵損失函式的實現
交叉熵損失函式 一般我們學習交叉熵損失函式是在二元分類情況下: L = −
【深度學習CV】SVM, Softmax損失函式
Deep learning在計算機視覺方面具有廣泛的應用,包括影象分類、目標識別、語義分隔、生成影象描述等各個方面。本系列部落格將分享自己在這些方面的學習和認識,如有問題,歡迎交流。 在使用卷積神經網路進行分類任務時,往往使用以下幾類損失函式: 平
python3__深度學習:TensorFlow__常用內建函式說明
tf.constant (value, dtype=None, shape=None, name="Const", verify_shape=False): 建立一個常數張量 value: 常數值,或list dtype: 結果張量中元素的型別 shape:
深度學習中softmax交叉熵損失函式的理解
1. softmax層的作用 通過神經網路解決多分類問題時,最常用的一種方式就是在最後一層設定n個輸出節點,無論在淺層神經網路還是在CNN中都是如此,比如,在AlexNet中最後的輸出層有1000個節點,即便是ResNet取消了全連線層,但1000個節點的輸出
分享《深入淺出深度學習:原理剖析與python實踐》PDF+源代碼
img color fff png aid pdf ffffff pytho 下載 下載:https://pan.baidu.com/s/1H4N0W5sPOE7YlK0KyC7TZQ 更多資料分享:http://blog.51cto.com/3215120 《深入淺出深度
《深入淺出深度學習:原理剖析與python實踐》pdf 下載
深入淺出深度學習:原理剖析與Python實踐》介紹了深度學習相關的原理與應用,全書共分為三大部分,第一部分主要回顧了深度學習的發展歷史,以及Theano的使用;第二部分詳細講解了與深度學習相關的基礎知識,包括線性代數、概率論、概率圖模型、機器學習和至優化演算法;在第三部分中,針對若干核心的深度
深度學習:反向傳播與基本原理
我們要證明得是這四個公式 有了這個四個公式,我們得反響傳播就可以遞推得到。 BP1公式: 這個是輸出層誤差方程,這個方程好像沒啥好說的 BP2公式 從這個公式我們可以通過高階層的誤差,
【NLP面試QA】啟用函式與損失函式
[TOC] #### Sigmoid 函式的優缺點是什麼 優點: - 輸出範圍優先,可以將任意範圍的輸出對映到 (0, 1) 範圍內,在輸出層可以用於表示二分類的輸出概率 - 易於求導 缺點: - Sigmoid 函式容易飽和,且梯度範圍為 (0, 0.25] ,在反向傳播中容易導致梯度消失問題。 ###
深度學習基礎--loss與啟用函式--合頁損失函式、摺頁損失函式;Hinge Loss;Multiclass SVM Loss
合頁損失函式、摺頁損失函式;Hinge Loss;Multiclass SVM Loss Hinge Loss是一種目標函式(或者說損失函式)的名稱,有的時候又叫做max-margin objective。用於分類模型以尋找距離每個樣本的距離最大的決策邊界,即最大化樣本和邊界之間的邊
深度學習筆記(三):啟用函式和損失函式
這一部分來探討下啟用函式和損失函式。在之前的logistic和神經網路中,啟用函式是sigmoid, 損失函式是平方函式。但是這並不是固定的。事實上,這兩部分都有很多其他不錯的選項,下面來一一討論 3. 啟用函式和損失函式 3.1 啟
深度學習:卷積神經網路,卷積,啟用函式,池化
卷積神經網路——輸入層、卷積層、啟用函式、池化層、全連線層 https://blog.csdn.net/yjl9122/article/details/70198357?utm_source=blogxgwz3 一、卷積層 特徵提取 輸入影象是32*32*3,3是它的深度(即R
Scala學習第六彈:函式與匿名函式
一、函式是第一等公民 Scala中,函式上升和變數同等的位置,或者說函式也是一種變數。 Scala中的函式可以作為實參傳遞給另一個函式; 函式可以作為返回值; 函式可以賦值給變數(這個變數需符合函式的型別的變數); 函式可以儲存在資料結構之中。 函式如同普通變數一樣,也具有
機器學習之損失函式與風險函式
1.損失函式與風險函式 監督學習的任務就是學習一個模型作為決策函式,對於給定的輸入X,給出相應的輸出f(X),這個輸出的預測值f(X)與真實值Y可能一致也可能不一致,用一個損失函式(lo
【深度學習基礎-09】神經網路-機器學習深度學習中~Sigmoid函式詳解
目錄 Sigmoid函式常常被用作神經網路中啟用函式 雙曲函式tanh(x) Logistic函式 拓展對比 Sigmoid函式常常被用作神經網路中啟用函式 函式的基本性質: 定義域:(−∞,+∞
深度學習:神經網路中的啟用函式
軟飽和和硬飽和sigmoid 在定義域內處處可導,且兩側導數逐漸趨近於0。Bengio 教授等[1]將具有這類性質的啟用函式定義為軟飽和啟用函式。與極限的定義類似,飽和也分為左飽和與右飽和。與軟飽和相對的是硬飽和啟用函式,即:f'(x)=0,當 |x| > c,其中 c 為常數。同理,硬飽和也分為左飽和
《深度學習:原理與應用實踐》中文版PDF
應用 href 書籍 nag tex 原理 圖片 water images 下載:https://pan.baidu.com/s/1YljEeog_D0_RUHjV6hxGQg 《深度學習:原理與應用實踐》中文版PDF,帶目錄和書簽; 經典書籍,講解詳細; 如圖: 《深度學
pytho系統學習:第二週之字串函式練習
# Author : Sunny# 雙下劃線的函式基本沒用# 定義字串name = 'i am sunny!'# 首字母大寫函式:capitalizeprint('-->capitalize:', name.capitalize())# 判斷結尾函式:endswithprint('-->endsw
分享《深度學習:原理與應用實踐》+PDF+張重生
ofo 51cto 經典 mar src mage 詳細 深度學習 目錄 下載:https://pan.baidu.com/s/1LmlYGbleDhkDAuqoZ2XjAQ更多資料分享:http://blog.51cto.com/14087171 《深度學習:原理與應用實