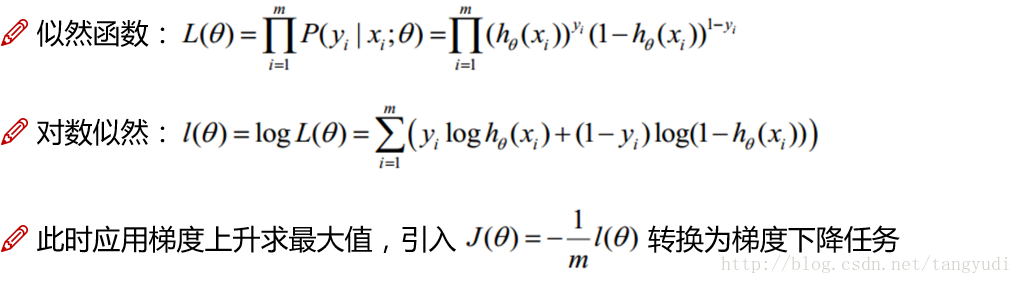一. 線性迴歸 VS 邏輯迴歸

線性迴歸，一般處理因變數是數值型區間變數（連續），用來擬合因變數和自變數之間的線性關係，但是因變數和自變數都是連續區間，常見的線性模型：

而在分析實際問題時，所研究問題變數不僅有區間變數（連續變數），也有屬性變數（分類變數 or 順序變數），如二項分佈問題，通過分析患者的年齡、性別、體質指數、平均血壓、疾病指數等指標，判斷一個人是否有糖尿病，Y = 0表未患病，Y = 1表患病，這裡的響應變數（分類變數）是一個兩點（0-1）分佈變數，它不能用h函式處理因變數是連續變數的問題，若因變數是定性（分類）問題，線性迴歸model就不能解決這個問題了，需要採用邏輯迴歸來解決定性（分類）問題。

邏輯迴歸，用來處理因變數為分類變數的迴歸問題，因為與迴歸問題非常相似，僅僅是輸出不一樣，所以稱為邏輯迴歸（邏輯迴歸用了和迴歸類似的方法來解決了分類問題），常見的是二分類問題，它也能處理多分類問題，邏輯迴歸實質是一種分類問題。

In short: 輸出變數型別是連續時，為線性迴歸（目標函式 均方誤差和），輸出變數型別是離散時，為邏輯迴歸（分類），目標函式（通常有正則項）

二. 邏輯迴歸  邏輯迴歸是一個非線性二分類（多分類）問題

對於一個邏輯迴歸問題（二分類問題），針對一個具體樣本，我們不僅僅想知道這個樣本屬於哪一類，同時還想知道屬於概率的概率是多大。對於線性迴歸和非線性迴歸的分類問題都不能回答這個問題，因為線性迴歸和非線性迴歸的為題，都是假設其分類函式如下：      Y  =  W * X  + b，因為Y的取值範圍是（負無窮大，正無窮大

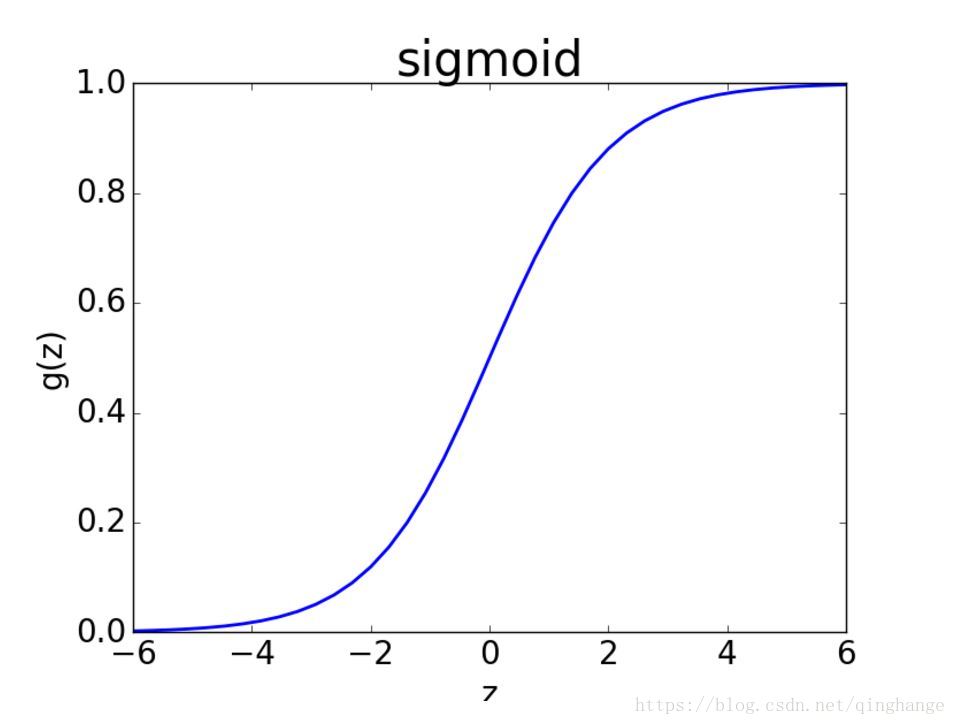
Sigmoid函式影象如下：

sigmoid函式完美的解決了上述需求，同時sigmoid函式連續可微

作用：將任意的輸入對映到[ 0, 1 ]區間，線性迴歸中得到一個預測值，then通過sigmoid函式對映到[ 0, 1]，實現值到分類概率的轉化

假設資料離散二類可分，分為0類和1類；當z值大於0的時候，sigmoid的概率大於1/2,表明偏向於類別1；反之則偏向於類別0。

閾值的選擇：

在沒有任何先驗條件的情況下，這裡的閾值一般選擇0.5。但當我們有進一步明確需求的時候，閾值也是可以調整的，例如我們希望對正例樣本有更高的準確率要求，則可以把閾值適當地調高，例如調高到0.6；相反，假如我們希望對正例樣本的召回率要求更高，則可以把閾值適當地降低，例如降低到0.4；

3. 引數估計---損失函式（Loss Function）和成本函式（Cost Function）

在二類分類中，假設sigmoid輸出結果表示屬於第 1 類的概率值，用的是均方損失函式

φ(z(i))表示sigmoid對第i個值的預測結果，我們將sigmoid函式帶入上述成本函式中，繪製其影象，發現這個成本函式的函式影象是一個非凸函式，如下圖所示，這個函式裡面有很多極小值，如果採用梯度下降法，則會導致陷入區域性最優解中,有沒有一個凸函式的成本函式呢？

假設sigmoid函式φ(z)表示屬於1類的概率，於是做出如下的定義：

將兩個式子綜合來，可以改寫為下式：

上式將分類為0和分類和1的概率計算公式合二為一。假設分類器分類足夠準確，此時對於一個樣本，如果它是屬於1類，分類器求出的屬於1類的概率應該儘可能大，即p(y=1lx)儘可能接近1；如果它是0類，分類器求出的屬於0類的概率應該儘可能大，即p(y=0lx)儘可能接近1。

4. 引數估計---極大似然法求解邏輯迴歸

藉助極大似然法估計引數w和b，對數似然函式並整理：

對於邏輯迴歸的求解，已然沿用我們上次跟大家討論的梯度下降演算法。給出似然函式，轉換對數似然（跟線性迴歸一致），但是我們現在的優化目標卻跟之前不太一樣了，線性迴歸的時候我們要求解的是最小值（最小二乘法），但是現在我們想得到的卻是使得該事件發生得最大值，為了沿用梯度下降來求解，可以做一個簡單的轉換新增一個負號以及一個常數很簡單的兩步就可以把原始問題依然轉換成梯度下降可以求解的問題。

邏輯迴歸是一個二分類演算法，那如果我的實際問題是一個多分類該怎麼辦呢？這個時候就需要Softmax啦，引入了歸一化機制，來將得分值對映成概率值。