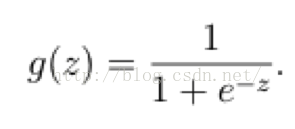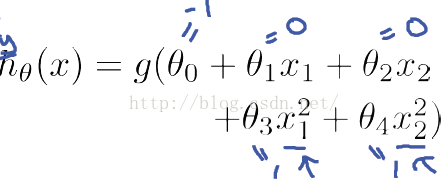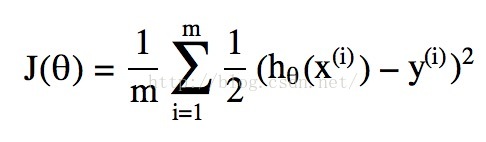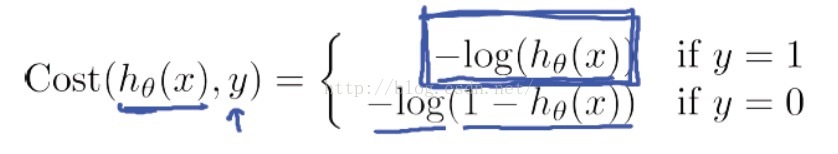1、總述

邏輯迴歸是應用非常廣泛的一個分類機器學習演算法，它將資料擬合到一個logit函式(或者叫做logistic函式)中，從而能夠完成對事件發生的概率進行預測。

2、由來

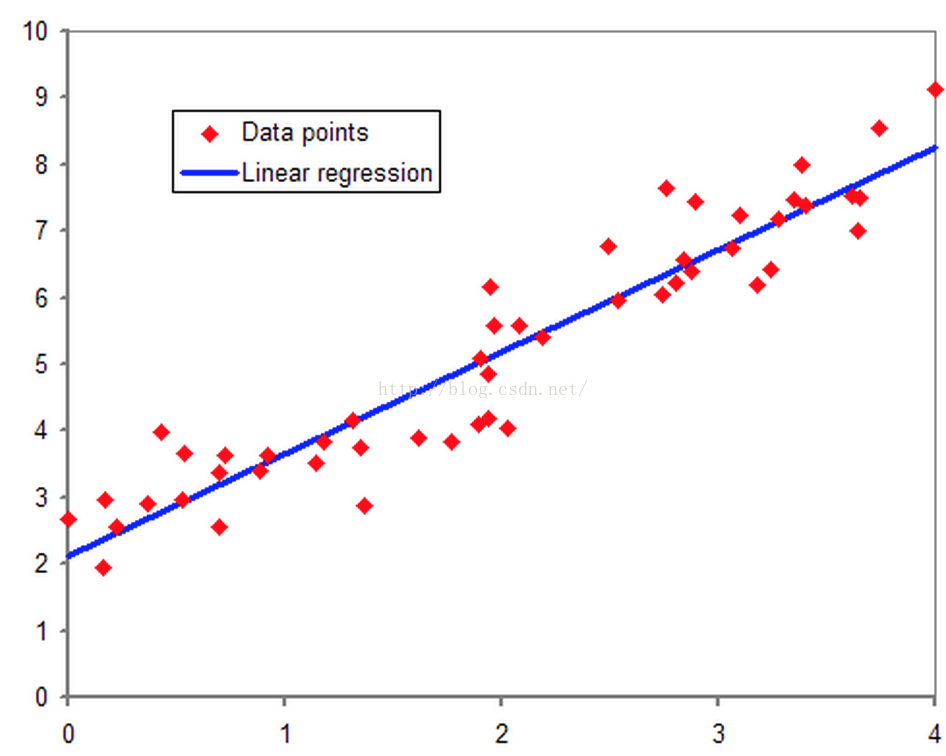
    要說邏輯迴歸，我們得追溯到線性迴歸，想必大家對線性迴歸都有一定的瞭解，即對於多維空間中存在的樣本點，我們用特徵的線性組合去擬合空間中點的分佈和軌跡。如下圖所示：

    線性迴歸能對連續值結果進行預測，而現實生活中常見的另外一類問題是，分類問題。最簡單的情況是是與否的二分類問題。比如說醫生需要判斷病人是否生病，銀行要判斷一個人的信用程度是否達到可以給他發信用卡的程度，郵件收件箱要自動對郵件分類為正常郵件和垃圾郵件等等。

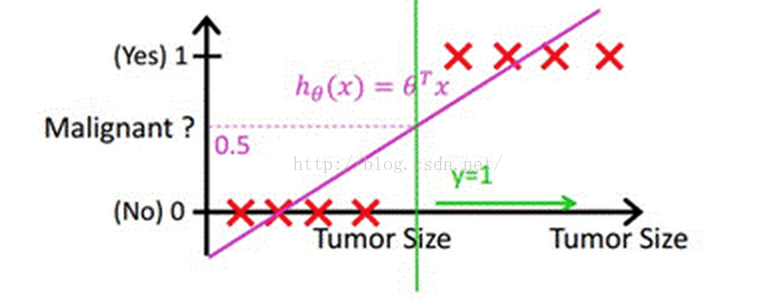
    當然，我們最直接的想法是，既然能夠用線性迴歸預測出連續值結果，那根據結果設定一個閾值是不是就可以解決這個問題了呢？事實是，對於很標準的情況，確實可以的，這裡我們套用Andrew Ng老師的課件中的例子，下圖中X為資料點腫瘤的大小，Y為觀測結果是否是惡性腫瘤。通過構建線性迴歸模型，如hθ(x)所示，構建線性迴歸模型後，我們設定一個閾值0.5，預測hθ(x)≥0.5的這些點為惡性腫瘤，而hθ(x)<0.5為良性腫瘤。

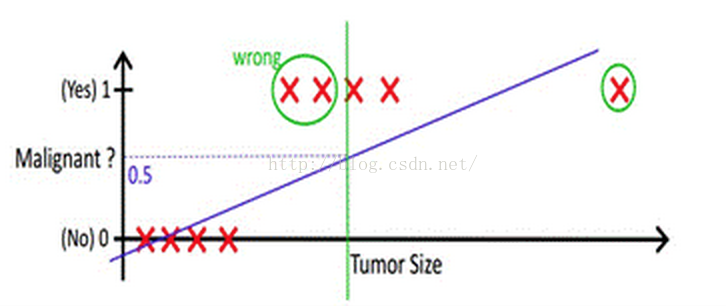
    但很多實際的情況下，我們需要學習的分類資料並沒有這麼精準，比如說上述例子中突然有一個不按套路出牌的資料點出現，如下圖所示：

    你看，現在你再設定0.5，這個判定閾值就失效了，而現實生活的分類問題的資料，會比例子中這個更為複雜，而這個時候我們藉助於線性迴歸+閾值的方式，已經很難完成一個魯棒性很好的分類器了。

    在這樣的場景下，邏輯迴歸就誕生了。它的核心思想是，如果線性迴歸的結果輸出是一個連續值，而值的範圍是無法限定的，那我們有沒有辦法把這個結果值對映為可以幫助我們判斷的結果呢。而如果輸出結果是 (0,1) 的一個概率值，這個問題就很清楚了。我們在數學上找了一圈，還真就找著這樣一個簡單的函數了，就是很神奇的sigmoid函式(如下)：

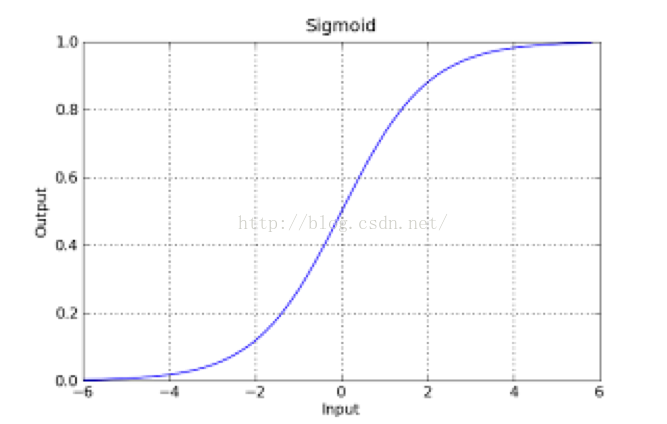
    如果把sigmoid函式影象畫出來，是如下的樣子：

Sigmoid Logistic Function

    從函式圖上可以看出，函式y=g(z)在z=0的時候取值為1/2，而隨著z逐漸變小，函式值趨於0，z逐漸變大的同時函式值逐漸趨於1，而這正是一個概率的範圍。

    所以我們定義線性迴歸的預測函式為Y=W^TX，那麼邏輯迴歸的輸出Y= g(W^TX)，其中y=g(z)函式正是上述sigmoid函式(或者簡單叫做S形函式)。

3、判定邊界

    我們現在再來看看，為什麼邏輯迴歸能夠解決分類問題。這裡引入一個概念，叫做判定邊界，可以理解為是用以對不同類別的資料分割的邊界，邊界的兩旁應該是不同類別的資料。

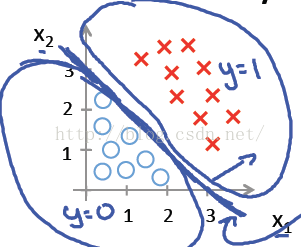
    從二維直角座標系中，舉幾個例子，大概是如下這個樣子：

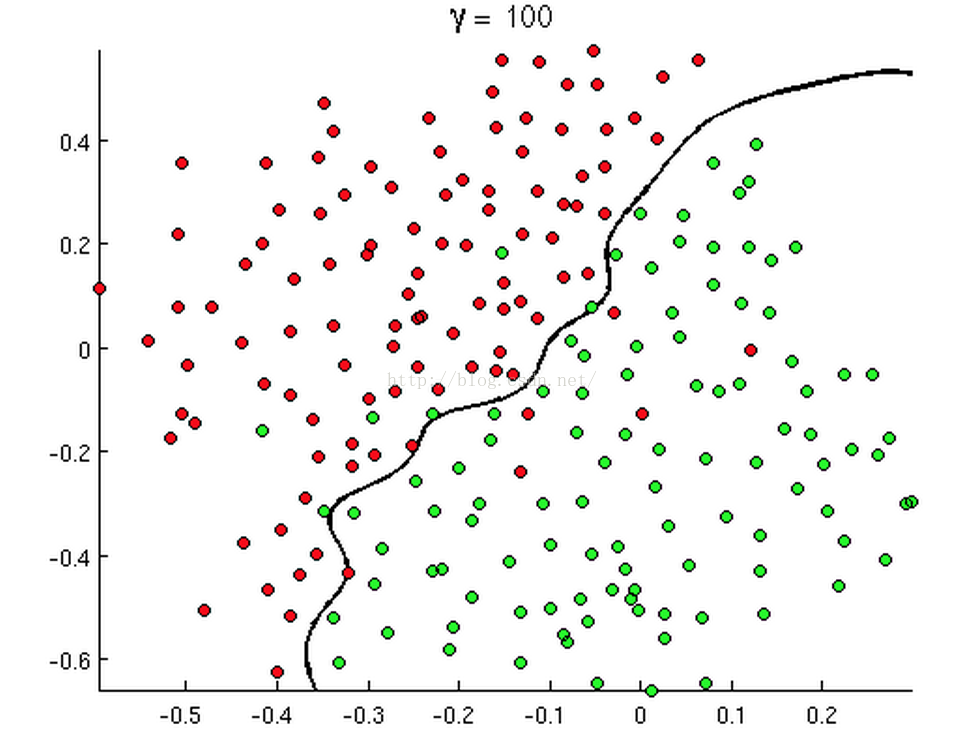
    有時候是這個樣子：

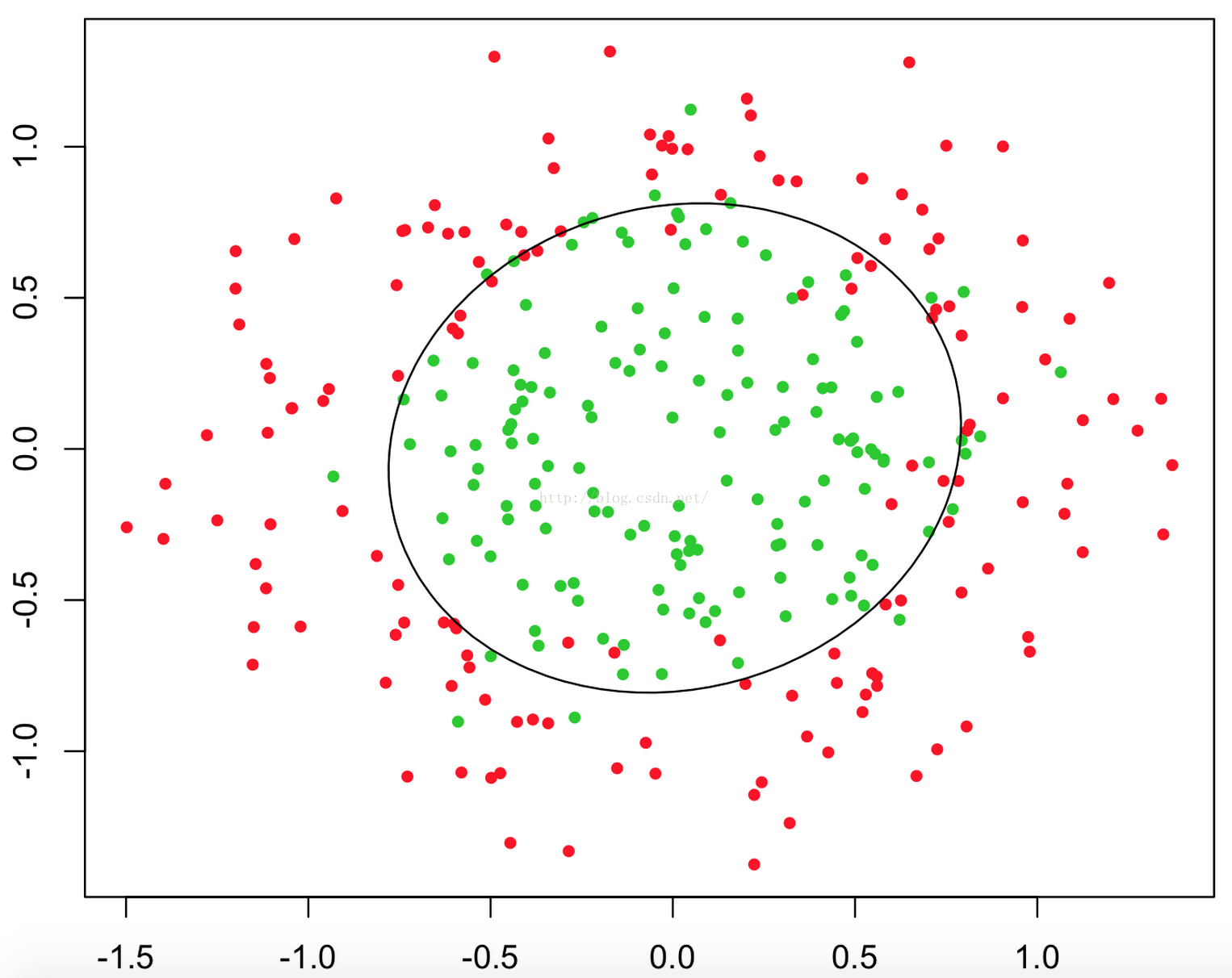
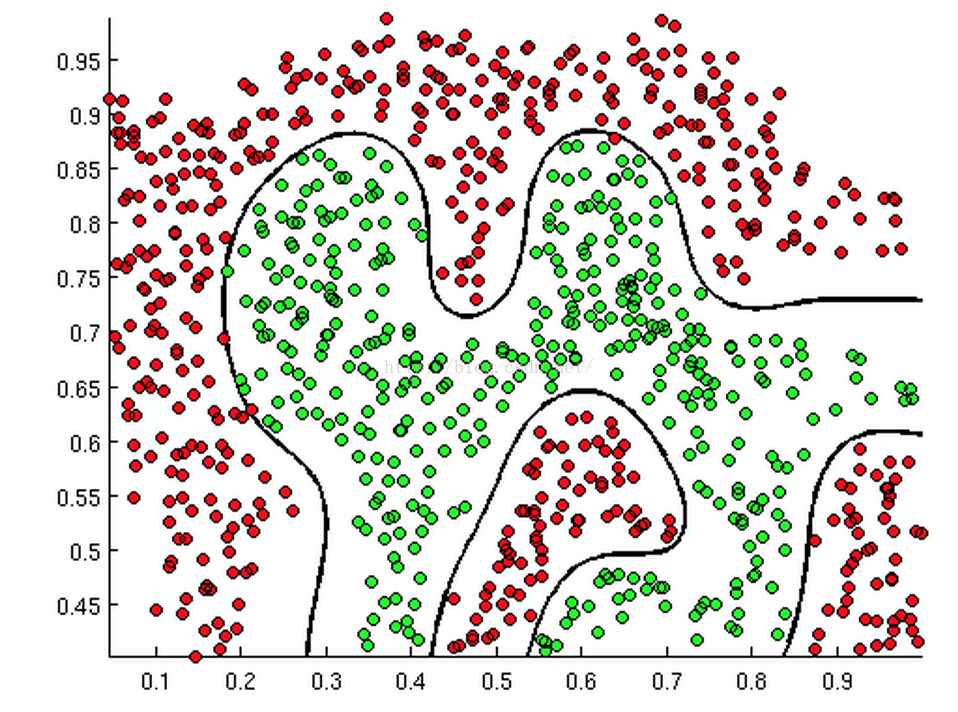
    甚至可能是這個樣子：

    上述三幅圖中的紅綠樣本點為不同類別的樣本，而我們劃出的線，不管是直線、圓或者是曲線，都能比較好地將圖中的兩類樣本分割開來。這就是我們的判定邊界，下面我們來看看，邏輯迴歸是如何根據樣本點獲得這些判定邊界的。

    我們依舊借用Andrew Ng教授的課程中部分例子來講述這個問題。

    回到sigmoid函式，我們發現：  

        當g(z)≥0.5時, z≥0;

        對於hθ(x)=g(θ^TX)≥0.5, 則θ^TX≥0, 此時意味著預估y=1;

        反之，當預測y = 0時，θ^TX<0;

    所以我們認為θ^TX =0是一個決策邊界，當它大於0或小於0時，邏輯迴歸模型分別預測不同的分類結果。

    先看第一個例子hθ(x)=g(θ₀+θ₁X₁+θ₂X₂)，其中θ_{0 ,}θ_{1 ,}θ₂分別取-3, 1, 1。則當−3+X₁+X₂≥0時, y = 1; 則X₁+X₂=3是一個決策邊界，圖形表示如下，剛好把圖上的兩類點區分開來：

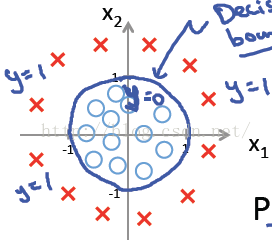
    例1只是一個線性的決策邊界，當hθ(x)更復雜的時候，我們可以得到非線性的決策邊界，例如：

    這時當x₁²+x₂²≥1時，我們判定y=1，這時的決策邊界是一個圓形，如下圖所示：

    所以我們發現，理論上說，只要我們的hθ(x)設計足夠合理，準確的說是g(θTx)中θTx足夠複雜，我們能在不同的情形下，擬合出不同的判定邊界，從而把不同的樣本點分隔開來。

4、代價函式與梯度下降

    我們通過對判定邊界的說明，知道會有合適的引數θ使得θTx=0成為很好的分類判定邊界，那麼問題就來了，我們如何判定我們的引數θ是否合適，有多合適呢？更進一步，我們有沒有辦法去求得這樣的合適引數θ呢？

    這就是我們要提到的代價函式與梯度下降了。

    所謂的代價函式Cost Function，其實是一種衡量我們在這組引數下預估的結果和實際結果差距的函式，比如說線性迴歸的代價函式定義為:

當然我們可以和線性迴歸類比得到一個代價函式，實際就是上述公式中hθ(x)取為邏輯迴歸中的g(θTx)，但是這會引發代價函式為“非凸”函式的問題，簡單一點說就是這個函式有很多個區域性最低點，如下圖所示：

而我們希望我們的代價函式是一個如下圖所示，碗狀結構的凸函式，這樣我們演算法求解到區域性最低點，就一定是全域性最小值點。

      因此，上述的Cost Function對於邏輯迴歸是不可行的，我們需要其他形式的Cost Function來保證邏輯迴歸的成本函式是凸函式。

      我們跳過大量的數學推導，直接出結論了，我們找到了一個適合邏輯迴歸的代價函式:

      Andrew Ng老師解釋了一下這個代價函式的合理性，我們首先看當y=1的情況：

       如果我們的類別y = 1, 而判定的hθ(x)=1，則Cost = 0，此時預測的值和真實的值完全相等，代價本該為0；而如果判斷hθ(x)→0，代價->∞，這很好地懲罰了最後的結果。

       而對於y=0的情況，如下圖所示，也同樣合理：

       下面我們說說梯度下降，梯度下降演算法是調整引數θ使得代價函式J(θ)取得最小值的最基本方法之一。從直觀上理解，就是我們在碗狀結構的凸函式上取一個初始值，然後挪動這個值一步步靠近最低點的過程，如下圖所示：

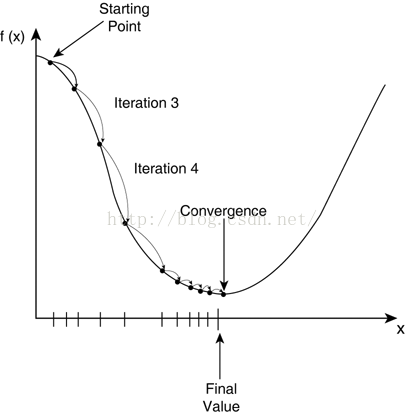
      我們先簡化一下邏輯迴歸的代價函式：

       從數學上理解，我們為了找到最小值點，就應該朝著下降速度最快的方向(導函式/偏導方向)邁進，每次邁進一小步，再看看此時的下降最快方向是哪，再朝著這個方向邁進，直至最低點。

       用迭代公式表示出來的最小化J(θ)的梯度下降演算法如下：

5、程式碼與實現

    我們來一起看兩個具體資料上做邏輯迴歸分類的例子，其中一份資料為線性判定邊界，另一份為非線性。

    示例1。

    第一份資料為data1.txt，部分內容如下：

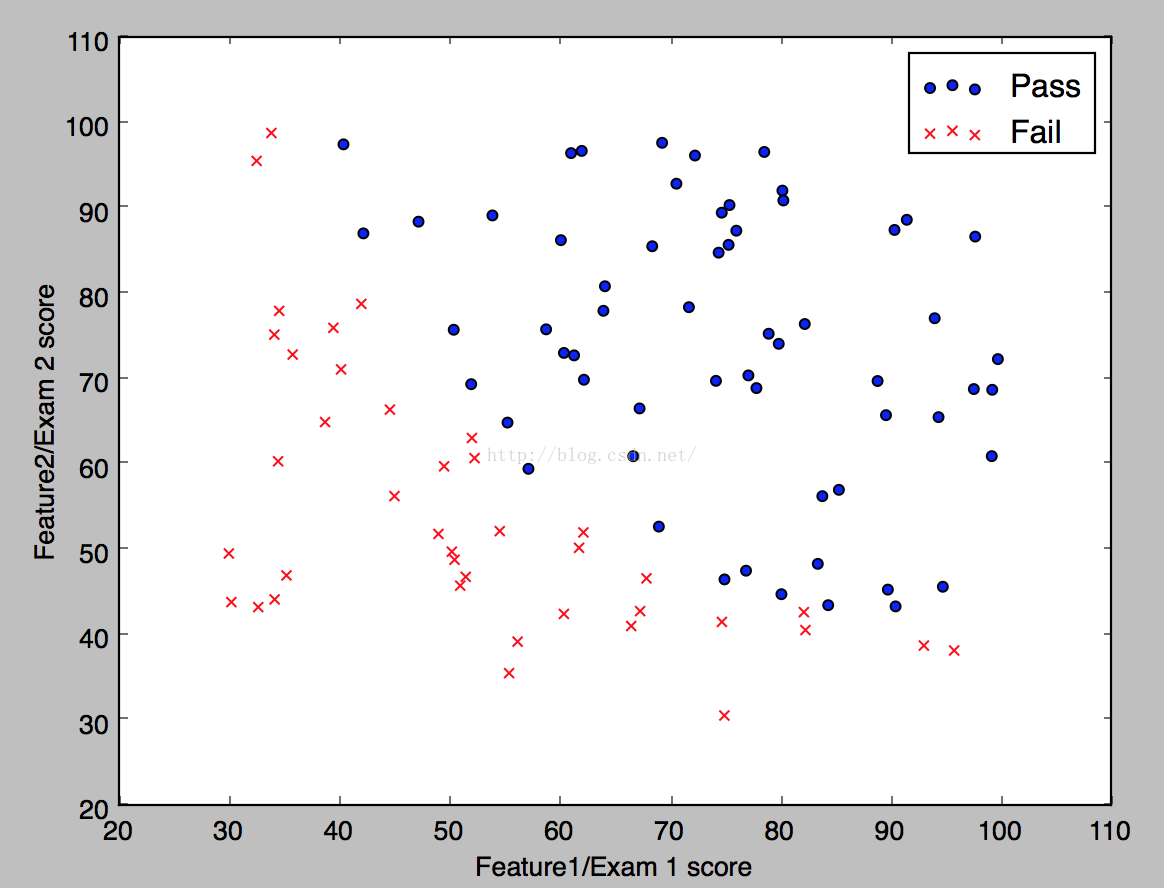
    我們先來看看資料在空間的分佈，程式碼如下。

1. from numpy import loadtxt, where  
2. from pylab import scatter, show, legend, xlabel, ylabel  
3. #load the dataset
4. data = loadtxt('/home/HanXiaoyang/data/data1.txt', delimiter=',')  
5. X = data[:, 0:2]  
6. y = data[:, 2]  
7. pos = where(y == 1)  
8. neg = where(y == 0)  
9. scatter(X[pos, 0], X[pos, 1], marker='o', c='b')  
10. scatter(X[neg, 0], X[neg, 1], marker='x', c='r')  
11. xlabel('Feature1/Exam 1 score')  
12. ylabel('Feature2/Exam 2 score')  
13. legend(['Fail', 'Pass'])  
14. show()  

    得到的結果如下：

    下面我們寫好計算sigmoid函式、代價函式、和梯度下降的程式：

1. def sigmoid(X):  
2.     '''''Compute sigmoid function '''
3.     den =1.0+ e **(-1.0* X)  
4.     gz =1.0/ den  
5.     return gz  
6. def compute_cost(theta,X,y):  
7.     '''''computes cost given predicted and actual values'''
8.     m = X.shape[0]#number of training examples
9.     theta = reshape(theta,(len(theta),1))  
10.     J =(1./m)*(-transpose(y).dot(log(sigmoid(X.dot(theta))))- transpose(1-y).dot(log(1-sigmoid(X.dot(theta)))))  
11.     grad = transpose((1./m)*transpose(sigmoid(X.dot(theta))- y).dot(X))  
12.     #optimize.fmin expects a single value, so cannot return grad
13.     return J[0][0]#,grad
14. def compute_grad(theta, X, y):  
15.     '''''compute gradient'''
16.     theta.shape =(1,3)  
17.     grad = zeros(3)  
18.     h = sigmoid(X.dot(theta.T))  
19.     delta = h - y  
20.     l = grad.size  
21.     for i in range(l):  
22.         sumdelta = delta.T.dot(X[:, i])  
23.         grad[i]=(1.0/ m)* sumdelta *-1
24.     theta.shape =(3,)  
25.     return  grad  

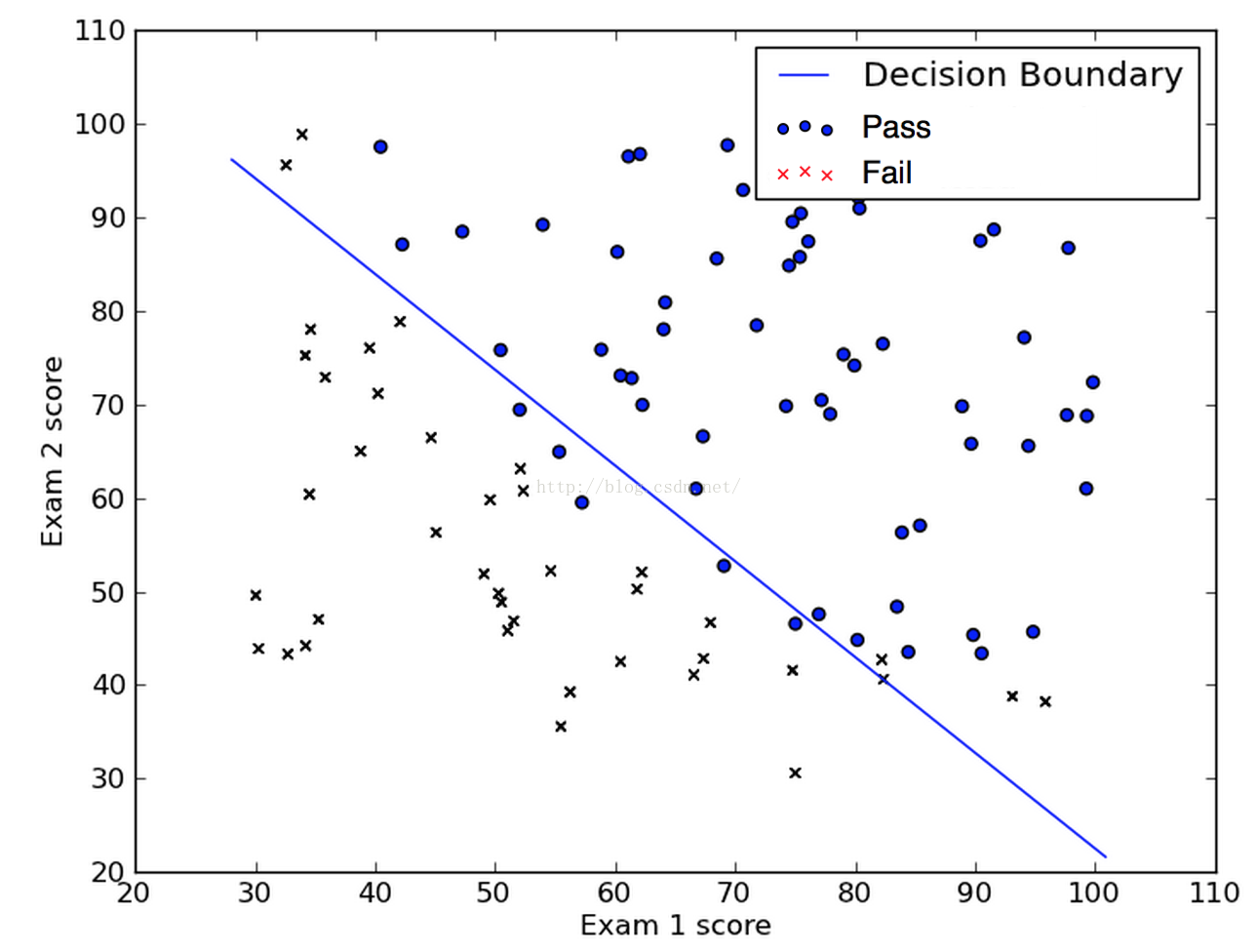
    我們用梯度下降演算法得到的結果判定邊界是如下的樣子：

    最後我們使用我們的判定邊界對training data做一個預測，然後比對一下準確率：

1. def predict(theta, X):  
2.     '''''Predict label using learned logistic regression parameters'''
3.     m, n = X.shape  
4.     p = zeros(shape=(m,1))  
5.     h = sigmoid(X.dot(theta.T))  
6.     for it in range(0, h.shape[0]):  
7.         if h[it]>0.5:  
8.             p[it,0]=1
9.         else:  
10.             p[it,0]=0
11.     return p  
12. #Compute accuracy on our training set
13. p = predict(array(theta), it)  
14. print'Train Accuracy: %f'%((y[where(p == y)].size / float(y.size))*100.0)  

    計算出來的結果是89.2%

    示例2.

    第二份資料為data2.txt，部分內容如下：

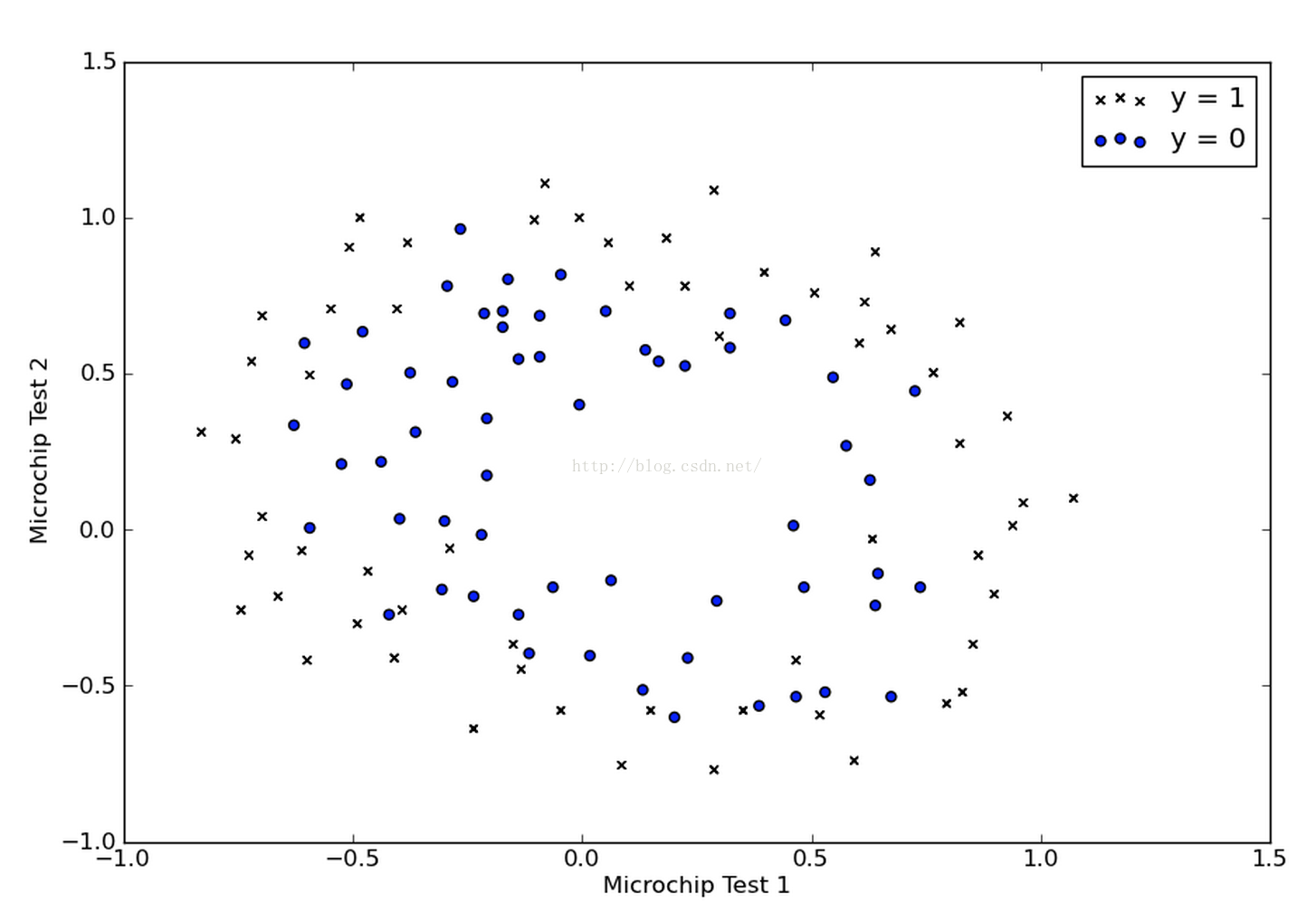
    我們同樣把資料的分佈畫出來，如下：

    我們發現在這個例子中，我們沒有辦法再用一條直線把兩類樣本點近似分開了，所以我們打算試試多項式的判定邊界，那麼我們先要對給定的兩個feature做一個多項式特徵的對映。比如說，我們做了如下的一個對映：

    程式碼如下：

1. def map_feature(x1, x2):  
2.     ''''' 
3.     Maps the two input features to polonomial features. 
4.     Returns a new feature array with more features of 
5.     X1, X2, X1 ** 2, X2 ** 2, X1*X2, X1*X2 ** 2, etc... 
6.     '''
7.     x1.shape =(x1.size,1)  
8.     x2.shape =(x2.size,1)  
9.     degree =6
10.     mapped_fea = ones(shape=(x1[:,0].size,1))  
11.     m, n = mapped_fea.shape  
12.     for i in range(1, degree +1):  
13.         for j in range(i +1):  
14.             r =(x1 **(i - j))*(x2 ** j)  
15.             mapped_fea = append(<span style="font-family: Arial, Helvetica, sans-serif;">mapped_fea</span><span style="font-family: Arial, Helvetica, sans-serif;">, r, axis=1)</span>  
16.     return mapped_fea  
17. mapped_fea = map_feature(X[:,0], X[:,1])  

      接著做梯度下降：

1. def cost_function_reg(theta, X, y, l):  
2.     '''''Compute the cost and partial derivatives as grads 
3.     '''
4.     h = sigmoid(X.dot(theta))  
5.     thetaR = theta[1:,0]  
6.     J =(1.0/ m)*((-y.T.dot(log(h)))-((1- y.T).dot(log(1.0- h)))) \  
7.             +(l /(2.0* m))*(thetaR.T.dot(thetaR))  
8.     delta = h - y  
9.     sum_delta = delta.T.dot(X[:,1])  
10.     grad1 =(1.0/ m)* sumdelta  
11.     XR = X[:,1:X.shape[1]]  
12.     sum_delta = delta.T.dot(XR)  
13.     grad =(1.0/ m)*(sum_delta + l * thetaR)  
14.     out = zeros(shape=(grad.shape[0], grad.shape[1]+1))  
15.     out[:,0]= grad1  
16.     out[:,1:]= grad  
17.     return J.flatten(), out.T.flatten()  
18. m, n = X.shape  
19. y.shape =(m,1)  
20. it = map_feature(X[:,0], X[:,1])  
21. #Initialize theta parameters
22. initial_theta = zeros(shape=(it.shape[1],1))  
23. #Use regularization and set parameter lambda to 1
24. l =1
25. # Compute and display initial cost and gradient for regularized logistic
26. # regression
27. cost, grad = cost_function_reg(initial_theta, it, y, l)  
28. def decorated_cost(theta):  
29.     return cost_function_reg(theta, it, y, l)  
30. print fmin_bfgs(decorated_cost, initial_theta, maxfun=500)  

      接著在資料點上畫出判定邊界：

1. #Plot Boundary
2. u = linspace(-1,1.5,50)  
3. v = linspace(-1,1.5,50)  
4. z = zeros(shape=(len(u), len(v)))  
5. for i in range(len(u)):  
6.     for j in range(len(v)):  
7.         z[i, j]=(map_feature(array(u[i]), array(v[j])).dot(array(theta)))  
8. z = z.T  
9. contour(u, v, z)  
10. title('lambda = %f'% l)  
11. xlabel('Microchip Test 1')  
12. ylabel('Microchip Test 2')  
13. legend(['y = 1','y = 0','Decision boundary'])  
14. show()  
15. def predict(theta, X):  
16.     '''''Predict whether the label 
17.     is 0 or 1 using learned logistic 
18.     regression parameters '''
19.     m, n = X.shape  
20.     p = zeros(shape=(m,1))  
21.     h = sigmoid(X.dot(theta.T))  
22.     for it in range(0, h.shape[0]):  
23.         if h[it]>0.5:  
24.             p[it,0]=1
25.         else:  
26.             p[it,0]=0
27.     return p  
28. #% Compute accuracy on our training set
29. p = predict(array(theta), it)  
30. print'Train Accuracy: %f'%((y[where(p == y)].size / float(y.size))*100.0)  

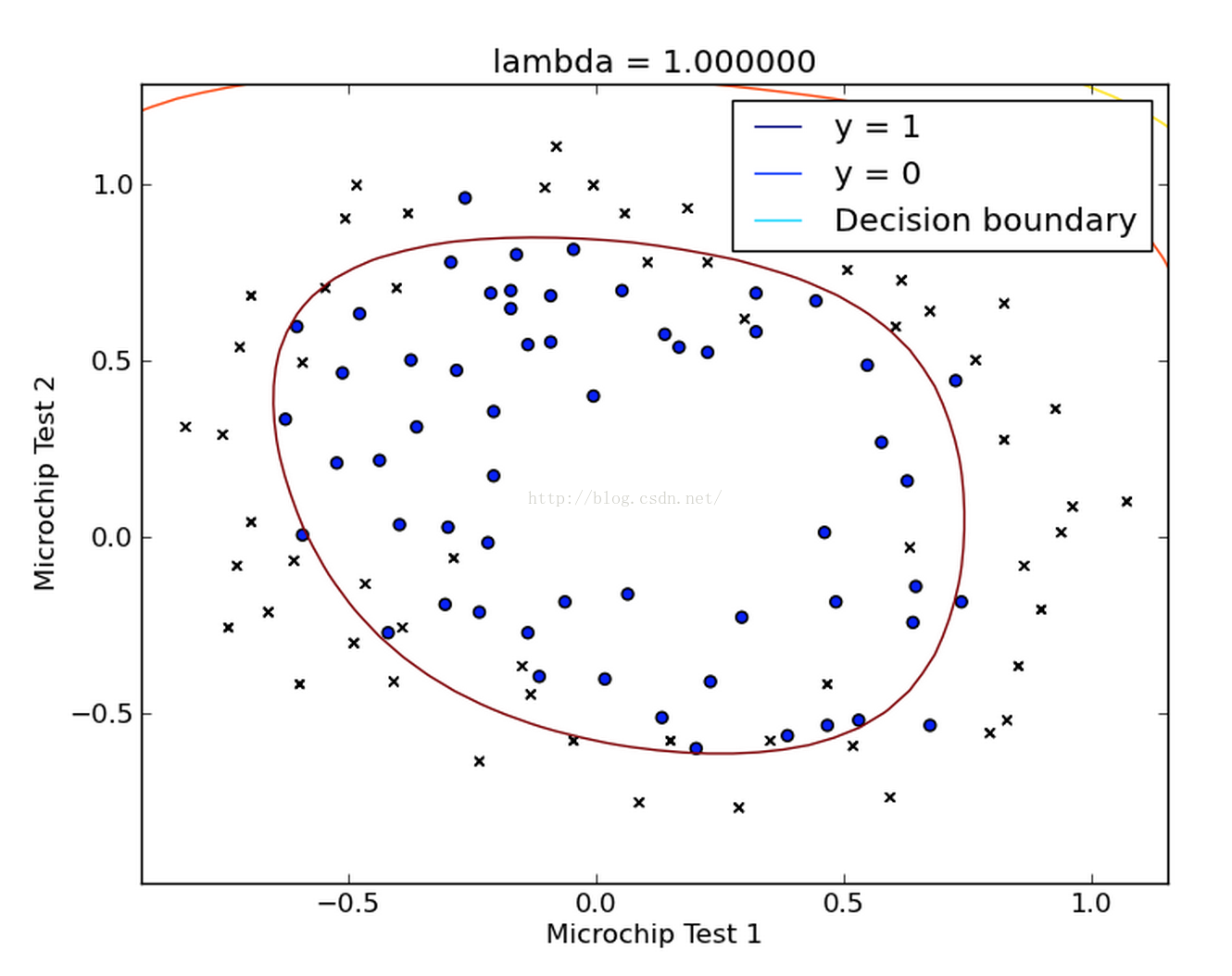
       得到的結果如下圖所示：

       我們發現我們得到的這條曲線確實將兩類點區分開來了。

6、總結

       最後我們總結一下邏輯迴歸。它始於輸出結果為有實際意義的連續值的線性迴歸，但是線性迴歸對於分類的問題沒有辦法準確而又具備魯棒性地分割，因此我們設計出了邏輯迴歸這樣一個演算法，它的輸出結果表徵了某個樣本屬於某類別的概率。

       邏輯迴歸的成功之處在於，將原本輸出結果範圍可以非常大的θ^TX 通過sigmoid函式對映到(0,1)，從而完成概率的估測。

        而直觀地在二維空間理解邏輯迴歸，是sigmoid函式的特性，使得判定的閾值能夠對映為平面的一條判定邊界，當然隨著特徵的複雜化，判定邊界可能是多種多樣的樣貌，但是它能夠較好地把兩類樣本點分隔開，解決分類問題。

       求解邏輯迴歸引數的傳統方法是梯度下降，構造為凸函式的代價函式後，每次沿著偏導方向(下降速度最快方向)邁進一小部分，直至N次迭代後到達最低點。

7、補充

      本文的2份資料可在http://pan.baidu.com/s/1pKxJl1p上下載到，分別為data1.txt和data2.txt，歡迎大家自己動手嘗試。