優化演算法

優化演算法的功能就是改善訓練方式，來最小化（最大化）損失函式

模型內部有些引數，是用來計算測試集中目標值 Y 的真實值和預測值的偏差，基於這些引數，就形成了損失函式E(x)。

比如說，權重($ω$)和偏差(b)就是這樣的內部引數，一般用於計算輸出值，在訓練神經網路模型時起到主要作用。

在有效地訓練模型併產生準確結果時，模型的內部引數起到了非常重要的作用。這也是為什麼我們應該用各種優化策略和演算法，來更新和計算影響模型訓練和模型輸出的網路引數，使其逼近或達到最優值。

優化演算法分為兩大類

一階優化演算法

這種演算法使用各引數的梯度值來最小化或最大化損失函式，最常用的一階優化演算法是梯度下降

函式梯度：導數 dy / dx 的多變量表達式，用來表示y相對於x的瞬時變化率。往往為了計算多變數函式的導數時，會用梯度取代導數，並使用偏導數來計算梯度。梯度和導數之間的一個主要區別是函式的梯度形成了一個向量場。

因此，對單變數函式，使用導數來分析；而梯度是基於多變數函式而產生的。更多理論細節在這裡不再進行詳細解釋。

隨機梯度下降法

經典的隨機梯度下降法（Stochastic Gradient Descent，簡稱SGD）是神經網路訓練的基本演算法，即每次批處理訓練時計算網路誤差並作誤差反向傳播，後根據一階梯度資訊對引數進行更新，其更新策略可表示為： $\omega_t =\omega_{t-1 }- \eta * \nabla{\omega_t})$

其中，一階梯度資訊 $\nabla{\omega_t}$ 完全依賴與當前批資料在網路目標函式上的誤差，故可以將學習率$\eta$理解為當前批的梯度對網路整體引數更新的影響程度。

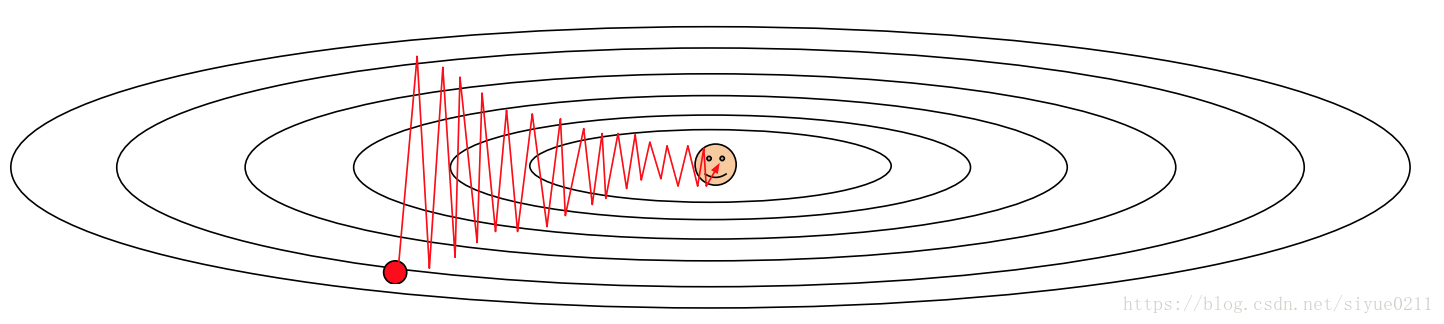
經典的隨機梯度下降是最常見的神經網路優化方法，收斂效果穩定，不過收斂速度慢。

• 為什麼收斂速度慢 因為梯度方向和較小值方向並不是在一條直線上，所以之字形的來回迭代 而且隨機梯度下降演算法容易陷在區域性最小值或者鞍點，區域性最小值在低維度的時候看著比較嚴重，但是在高緯度時鞍點才是核心問題。因為高緯度的時候，引數就有上千個，不同引數的變化很容易造成某些緯度損失增大，某些緯度損失減小，總的損失很小

###基於動量的隨機梯度下降法 隨機梯度下降演算法是非常受歡迎的優化方法，但學習過程會有時很慢。動量方法旨在加速學習，特別是處理高曲率，小但一致的梯度或是帶噪聲的梯度。動量的方法積累了之前梯度指數級衰減的移動平均，並且沿著該方向移動。

上圖為沒有動量，下圖為有動量，可以看出動量相當於在連續梯度指向相同方向時，加大步長。我們可以將梯度下降比喻成一個小球在冰上，每當它沿著表面最抖的部分下降時，它會累計繼續在該方向上滑行的速度，直到其開始向上滑為止。在上滑時步長變小。 公式為： $v_t = \mu * v_{t-1} - \eta * g$ $\omega_t = \omega_{t-1} + v_t$

這個公式和SDG的區別其實就是加上了一個$\mu * v_{t-1}$ 其中$\mu$為動量因子，控制動量資訊對整體梯度更新的影響程度，一般取值0.5, 0.9, 0.99。 基於動量的隨機梯度下降演算法除了可以抑制震盪，還可以在網路訓練後期趨於收斂，網路引數在區域性最小值附近來回震盪時幫助其跳出區域性限制。 當其梯度指向實際移動方向時，動量項$v$增大；當梯度與實際移動方向相反時，$v$減小。這種方式意味著動量項只對相關樣本進行引數更新，減少了不必要的引數更新，從而得到更快且穩定的收斂，也減少了振盪過程。 ###Nesterov型動量隨機下降法 Nesterov型動量隨機梯度下降方法是在上述動量梯度下降法更新梯度時加入對當前梯度的校正。相比一般動量方法，Nesterov型動量法對於凸函式在收斂性上有更強的理論保證。同時，Nesterov型動量也有更好的表現。 自己理解：動量隨機梯度下降法從公式上看應該只是對於連續梯度指向同一個方向時，加大步長。而Nesterov是不僅僅改變步長，而且還對梯度方向進行調整。 $\omega_{ahead} = \omega_{t-1} + \mu * v_{t-1}$ $v_t = \mu * v_{t-1} - \eta * \nabla_{\omega_{ahead}}$ $\omega_t = \omega_{t-1} + v_t$

Require：學習率η, 動量引數μ
Require:初始引數w，初始速度v
   while 沒有達到停止條件準則 do
     從訓練集中找m個樣本X={x1，x2...xm}的小批量，對應目標yi
     應用臨時更新： w' = w + μv
     計算梯度（在臨時點）g = 1/m ▽w'
     計算速度更新： v =  μ*v- η*g
     應用更新：w = w + v

###Adagrad Adagrad 能獨立地適應所有模型引數的學習率，縮放每個引數反比與其它所有梯度歷史平方值總和的平方根。具有損失最大偏導的引數相應地有一個快速下降的學習率，而具有小偏導的引數在學習率上有相對較小的下降。淨效果是在引數空間中更為平緩的傾斜方向會取得更大進步。 AdaGrad演算法具有一些令人滿意的理論性質。然而，經驗上已經發現，對於訓練神經網路模型而言，從訓練開始累計梯度平方會導致有效的學習率過早和過量的減小。

Require:全域性學習率η
Require:初始引數w
Require：小常數δ， 為了數值穩定大約設定為10^-7
  初始化梯度累計變數 r=0
  while 沒有達到停止準則 do
    從訓練集中採包含m個樣本X={x1，x2...xm}的小批量，對應目標yi
    計算梯度（在臨時點）g = 1/m ▽w'
    累積平方梯度： r = r + g*g (g 和 g逐元素相乘)
    計算更新 w' = η / (δ + sqrt(r))*g
    應用更新 w = w + w'
 end while

###RMSProp RMSProp改進了Adagrad在訓練開始就累計梯度平方會導致有效的學習率過早和過量的減少。

Require:全域性學習率η, 衰減速率ρ
Require:初始引數w
Require：小常數δ， 為了數值穩定大約設定為10^-6
  初始化梯度累計變數 r=0
  while 沒有達到停止準則 do
    從訓練集中採包含m個樣本X={x1，x2...xm}的小批量，對應目標yi
    計算梯度（在臨時點）g = 1/m ▽w'
    累積平方梯度： r = ρr + (1-ρ)g*g (g 和 g逐元素相乘)
    計算更新 w' = η / (δ + sqrt(r))*g
    應用更新 w = w + w'
 end while

RMSProp使用指數衰減平均以丟棄遙遠過去的歷史，使其能夠找到凹碗之後快速收斂。 ###使用Nesterov動量的RMSProp演算法

Require:全域性學習率η, 衰減速率ρ, 動量係數μ
Require:初始引數w， 初始引數v
Require：小常數δ， 為了數值穩定大約設定為10^-6
  初始化梯度累計變數 r=0
  while 沒有達到停止準則 do
    從訓練集中採包含m個樣本X={x1，x2...xm}的小批量，對應目標yi
    應用臨時更新： w' = w + μv
    計算梯度（在臨時點）g = 1/m ▽w'
    累積平方梯度： r = ρr + (1-ρ)g*g (g 和 g逐元素相乘)
    計算更新 w' = μ * v - η / (sqrt(r))*g
    應用更新 w = w + w'
 end while

二階優化演算法

二階優化演算法使用了二階導數(也叫做Hessian方法)來最小化或最大化損失函式。由於二階導數的計算成本很高，所以這種方法並沒有廣泛使用。

深度卷積神經網路通常採用隨機梯度下降型別的優化演算法進行模型訓練和引數求解。經過近些年相關領域的發展，出現了一系列有效的網路訓練優化新演算法。許多工具箱都提供了了這些優化演算法，工程實踐中只需要根據自身的任務的需求選擇合適的優化演算法即可。 以下介紹為了簡化起見，我們假設待學習引數$\omega$，學習率或步長為$\eta$，一階梯度值為$g$，$t$表示第t輪訓練。

###Adam

Require: 步長η（預設為：0.001）
Require: 距估計的指數衰減速率，ρ1和ρ2在區間[0, 1)內，建議0.9 / 0.99
Require：用於數值穩定的小常數δ(建議預設為10^-8)
Require: 初始引數w
 初始化一階和二階矩變數 s=0， r=0
 初始化時間步t=0
 while沒有達到停止準則 do
   從訓練集中採包含m個樣本X={x1，x2...xm}的小批量，對應目標yi
   計算梯度（在臨時點）g <- 1/m ▽w'
   t <- t+1
   更新有偏一階距估計： s <- ρ1*s + (1 - ρ1)g
   更新有偏二階距估計： r <- ρ2*r + (1 - ρ2)g*g  (*表示點乘)
   更新一階矩的偏差：s' <- s / (1 - ρ1(t))
   更新二階矩的偏差：r' <- r / (1 - ρ2(t))
   計算更新：w' = -η * s' / ()sqrt(r')+δ)
   應用更新 w <- w + w'
 end while

##微調神經網路 除了從頭訓練自己的網路之外，一種更加有效，高效的方法是微調已訓練好的網路模型。微調預訓練模型簡單有效，就是用目標任務資料在原先預訓練模型上繼續進行訓練過程。

1. 由於網路在原始資料集上已經收斂，因此應設定較小的學習率在目標資料上微調，如$10^{-4}$數量級以下。
2. 卷積神經網路淺層擁有更泛化的特徵（如邊緣，紋理等），深層的特徵則更抽象對應高層語義。因此，在新資料上微調時泛化特徵更新可能或程度很小，高層語義特徵更新可能程度較大，故可根據層神對不同層設定不同學習率：網路深層的學習率可稍大於淺層學習率
3. 根據目標任務資料與原始資料相似程度採用不同微調策略： a) 當目標資料較少且目標資料與原始資料非常相似時，可僅微調網路靠近目標函式的後幾層； b) 當目標資料充足且相似時，可微調更多網路層，也可全部微調； c) 當目標資料充足但與原始資料差異較大，此時須多調節一些網路層，直至微調全部； d) 當目標資料極少，同時還與原始資料有較大差異時，這種情形比較麻煩，微調成功與否要具體 問題具體對待，不過仍可嘗試首先微調網路後幾層後再微調整個網路模型。

針對“當目標資料極少，同時還與原始資料有較大差異時”的情況，目前比較有效的方式是藉助部分原始資料與目標資料協同訓練。Ge和Yu提出，因預訓練模型的淺層網路特徵更具有泛化力，故可在淺層空間選擇目標資料的近鄰作為原始資料子集。之後，將微調階段改為多工學習（多工學習就是有兩個不同的任務，用同一個網路，同時生成兩個結果）：一者將目標任務基於原始資料子集，二者將目標任務基於全部目標資料。

##參考文獻 [1] 解析卷積神經網路——深度學習實踐手冊 [2] 深度學習（花書）