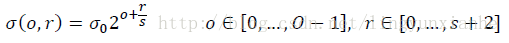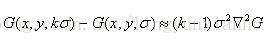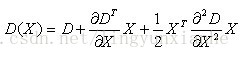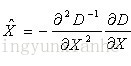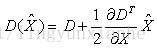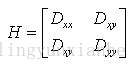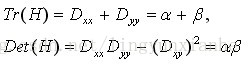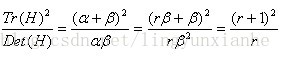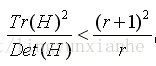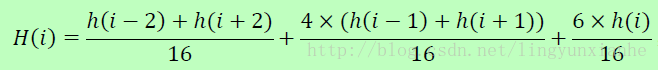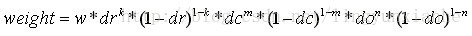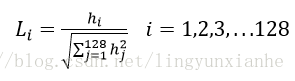計算機視覺中的特徵點提取演算法比較多，但SIFT除了計算比較耗時以外，其他方面的優點讓其成為特徵點提取演算法中的一顆璀璨的明珠。SIFT演算法的介紹網上有很多比較好的部落格和文章，我在學習這個演算法的過程中也參看網上好些資料，即使評價比較高的文章，作者在文章中對有些比較重要的細節、公式來歷沒有提及，可能寫部落格的人自己明白，也覺得簡單，因此就忽略了這些問題，但是對剛入門的人來說，看這些東西，想搞清楚這些是怎麼來的還是比較費時費力的。比如SIFT演算法中一個重要的操作：求取描述子的主方向。好多文章只是一提而過或忽略，然後直接給出一個公式，SIFT演算法的原作者也提使用拋物線插值，但是具體怎麼插的就不太詳盡了，對於初學者來說更是不知所云。因此本文打算在參看的文章上對有關這些細節給出一些比較詳細的說明，還有本文儘量對操作過程配備對應圖片或示意圖說明，同時附上robwhesss開源SIFT C程式碼對應程式塊並給予註解，方便理解。    

一、 SIFT演算法

1、演算法簡介

尺度不變特徵轉換即SIFT (Scale-invariant feature transform)是一種計算機視覺的演算法。它用來偵測與描述影像中的區域性性特徵，它在空間尺度中尋找極值點，並提取出其位置、尺度、旋轉不變數，此演算法由 David Lowe在1999年所發表，2004年完善總結。

       其應用範圍包含物體辨識、機器人地圖感知與導航、影像縫合、3D模型建立、手勢辨識、影像追蹤和動作比對。

      區域性影像特徵的描述與偵測可以幫助辨識物體，SIFT特徵是基於物體上的一些區域性外觀的興趣點而與影像的大小和旋轉無關。對於光線、噪聲、些微視角改變的容忍度也相當高。基於這些特性，它們是高度顯著而且相對容易擷取，在母數龐大的特徵資料庫中，很容易辨識物體而且鮮有誤認。使用 SIFT特徵描述對於部分物體遮蔽的偵測率也相當高，甚至只需要3個以上的SIFT物體特徵就足以計算出位置與方位。在現今的電腦硬體速度下和小型的特徵資料庫條件下，辨識速度可接近即時運算。SIFT特徵的資訊量大，適合在海量資料庫中快速準確匹配。

      SIFT演算法的實質是在不同的尺度空間上查詢關鍵點(特徵點)，並計算出關鍵點的方向。SIFT所查詢到的關鍵點是一些十分突出，不會因光照，仿射變換和噪音等因素而變化的點，如角點、邊緣點、暗區的亮點及亮區的暗點等。

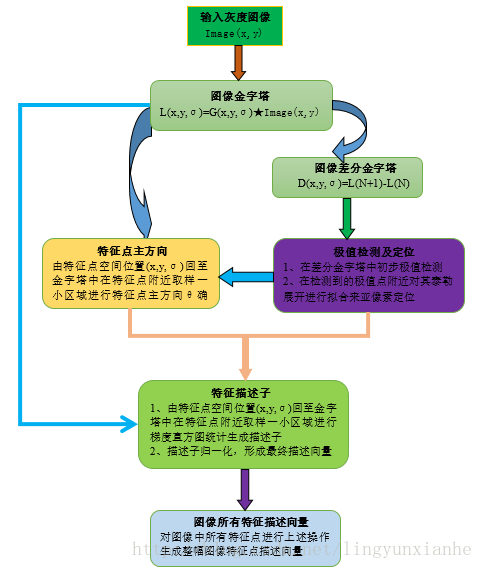
2、SIFT演算法流程圖

     

二、SIFT演算法操作步驟

1、影象金字塔

1.1、高斯金字塔

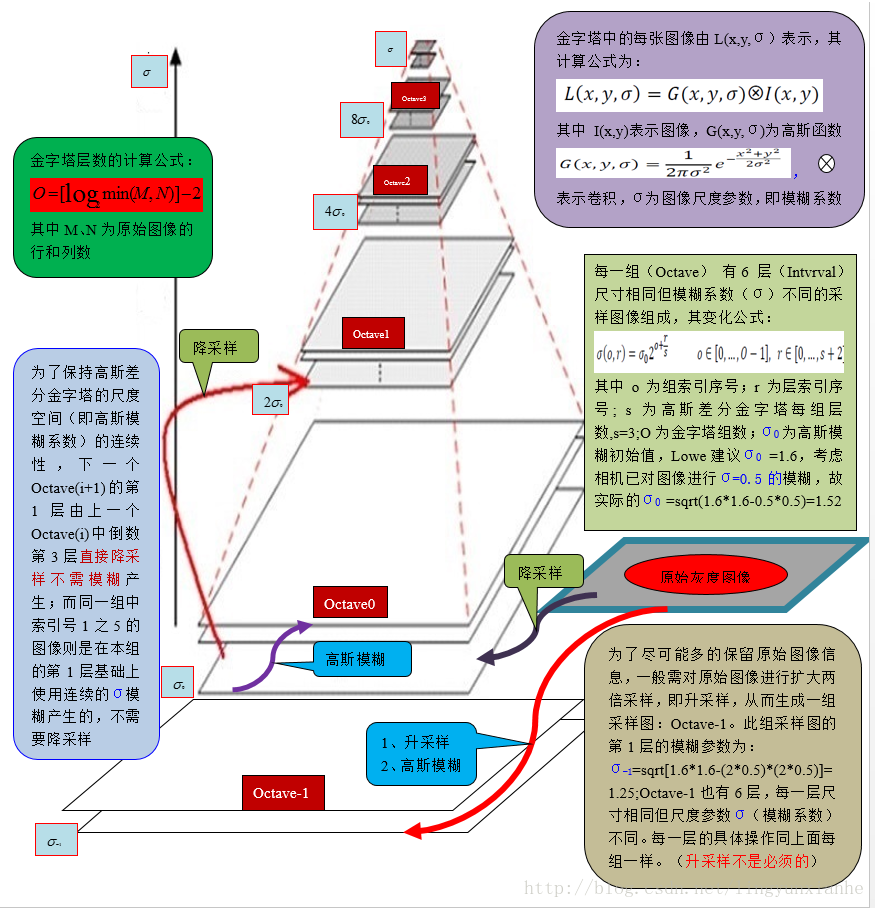
影象高斯金字塔(Gaussian Pyramid)是採用高斯函式對影象進行模糊以及降取樣處理得到。其形成過程可如下圖所示：    

其中高斯模糊係數計算公式如下：

其中高斯模糊係數計算公式如下：

1.1.1、高斯函式與影象卷積

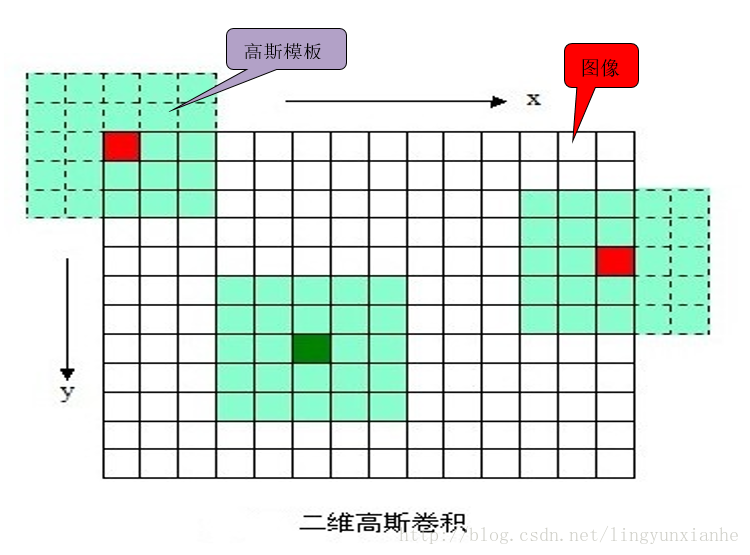
根據3σ原則，使用NxN的模板在影象每一個畫素點處操作，其中N=[（6σ+1）]且向上取最鄰近奇數。

其操作如下圖：

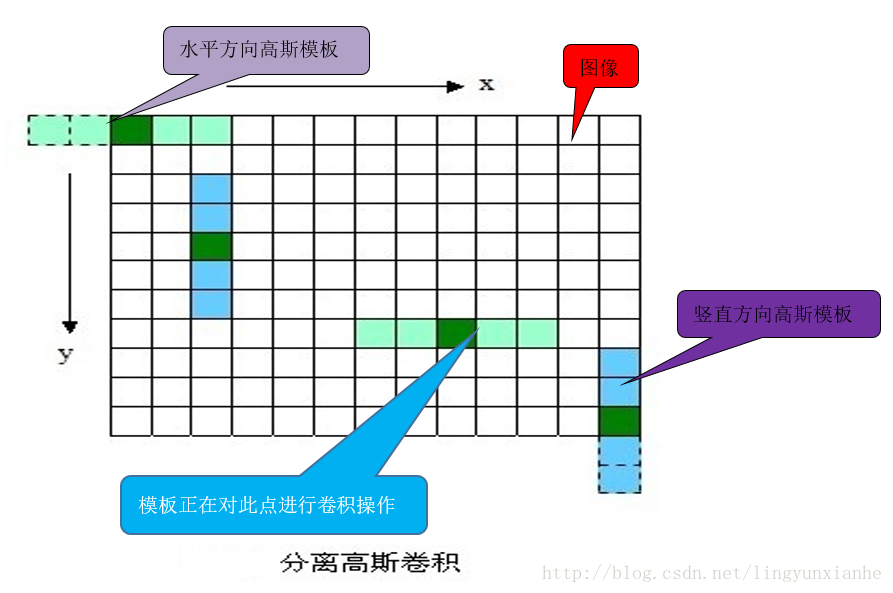
1.1.2、分離高斯卷積

上面這樣直接與影象卷積，速度比較慢，同時影象邊緣資訊也會損失嚴重。後來，後來、、、，不知哪位學者發現，可以使用分離的高斯卷積（即先用1xN的模板沿著X方向對影象卷積一次，然後用Nx1的模板沿著Y方向對影象再卷積一次，其中N=[（6σ+1）]且向上取最鄰近奇數），這樣既省時也減小了直接卷積對影象邊緣資訊的嚴重損失。

1.1.3、高斯金子塔原始碼分析

for (o = 0; o < octvs; o++)//金字塔組數為octvs，
	for (i = 0; i < intvls + 3; i++)//每一組有intvls + 3 層，intvls一般為3
		{
		if (o == 0 && i == 0)//如果是第一組第1層
			gauss_pyr[o][i] = cvCloneImage(base);//base 為原始灰度影象經過升取樣或降取樣得到的影象
	/* base of new octvave is halved image from end of previous octave */
		else if (i == 0)//建立非第一組的第1層
			gauss_pyr[o][i] = downsample(gauss_pyr[o - 1][intvls]);//降取樣影象
		/* blur the current octave's last image to create the next one */
		else//建立非第一組的非第1層
			{
			gauss_pyr[o][i] = cvCreateImage(cvGetSize(gauss_pyr[o][i - 1]),IPL_DEPTH_32F, 1);
			cvSmooth(gauss_pyr[o][i - 1], gauss_pyr[o][i],CV_GAUSSIAN, 0, 0, sig[i], sig[i]);// sig[i]為模糊係數
			}//cvSmooth 為平滑處理函式，也即模糊處理。CV_GAUSSIAN 為選用高斯函式對影象模糊
	return gauss_pyr;//返回建好的金字塔

1.2、高斯差分金字塔

2002年Mikolajczyk在詳細的實驗比較中發現尺度歸一化的高斯拉普拉斯函式的極大值和極小值同其它的特徵提取函式，例如：梯度，Hessian或Harris角特徵比較，能夠產生最穩定的影象特徵。而Lindeberg早在1994年就發現高斯差分函式（簡稱DOG運算元）與尺度歸一化的高斯拉普拉斯函式非常近似。如下式：

其中k-1是個常數，並不影響極值點位置的求取。

1.2.1、差分金字塔的建立

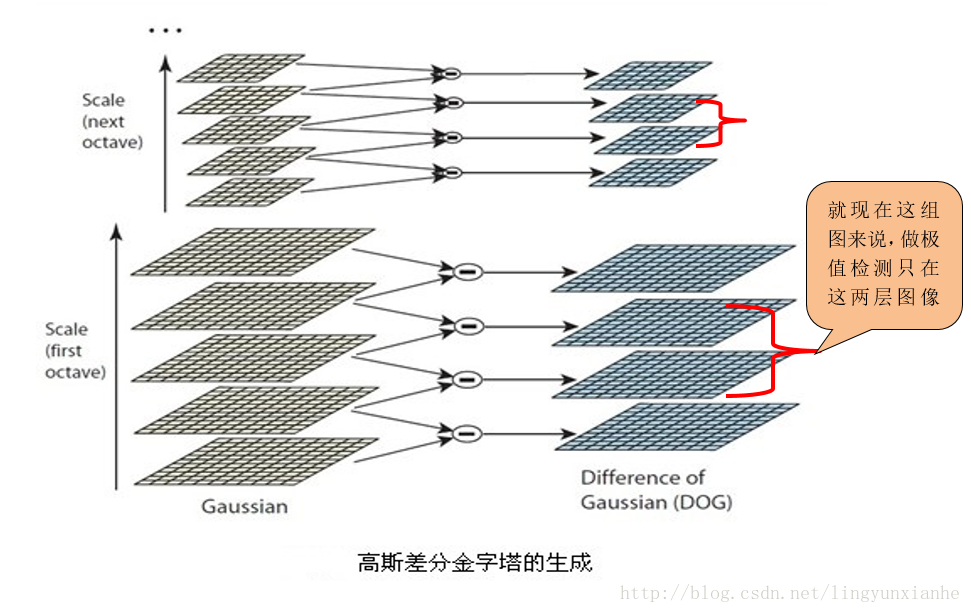
差分金字塔的是在高斯金字塔的基礎上操作的，其建立過程是：在高斯金子塔中的每組中相鄰兩層相減（下一層減上一層）就生成高斯差分金字塔.

高斯差分金字塔其操作如下圖：

1.2.2、差分金字塔原始碼分析

for (o = 0; o < octvs; o++)//octvs為高斯金字塔組數
	for (i = 0; i < intvls + 2; i++)//因為相減，故高斯金字塔中每組有（intvls + 2）層影象
		{
		dog_pyr[o][i] = cvCreateImage(cvGetSize(gauss_pyr[o][i]),IPL_DEPTH_32F, 1);
		cvSub(gauss_pyr[o][i + 1], gauss_pyr[o][i], dog_pyr[o][i], NULL);//cvSub為opencv內建相減函式
		}
	return dog_pyr;//返回高斯差分金字塔
 

2、空間極值點（即關鍵點）檢測

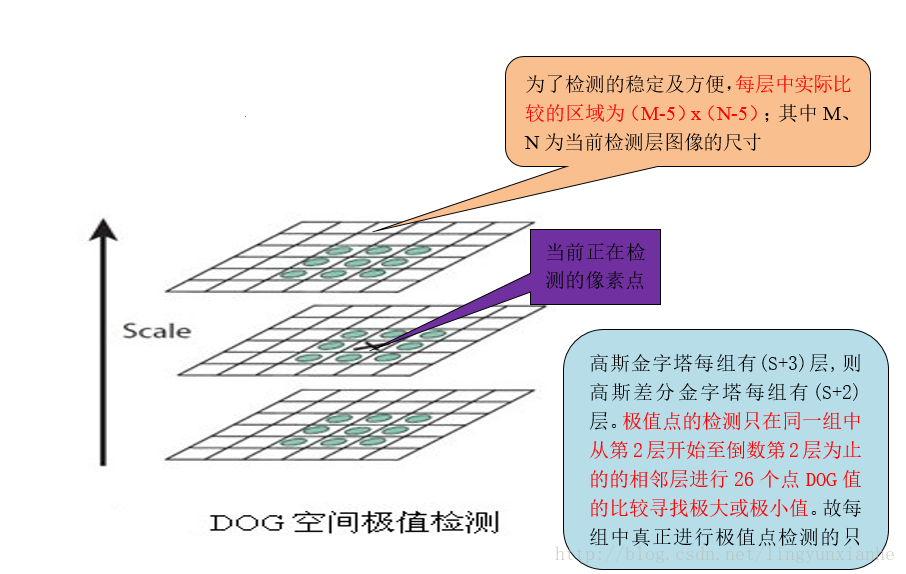
關鍵點是由DOG空間的區域性極值點組成的，關鍵點的初步探查是通過同一組內各DoG相鄰兩層影象之間比較完成的。為了尋找DoG函式的極值點，每一個畫素點要和它所有的相鄰點比較，看其是否比它的影象域和尺度域的相鄰點大或者小。如圖下圖所示，中間的檢測點和它同尺度的8個相鄰點和上下相鄰尺度對應的9×2個點共26個點比較，以確保在尺度空間和二維影象空間都檢測到極值點。

2.1、極值點檢測過程

2.1.1、極值點檢測示意

2.1.2、極值點檢測原始碼分析

if (val > 0)//極大值檢測{

for (i = -1; i <= 1; i++)

for (j = -1; j <= 1; j++)

for (k = -1; k <= 1; k++)

if (val < pixval32f(dog_pyr[octv][intvl + i], r + j, c + k))//pixval32f為提取影象畫素位置上的灰度值

return 0;}

else /* check for minimum */

{

for (i = -1; i <= 1; i++)

for (j = -1; j <= 1; j++)

for (k = -1; k <= 1; k++)

if (val > pixval32f(dog_pyr[octv][intvl + i], r + j, c + k))//r c為影象的行數和列數，dog_pyr為高斯差分圖

return 0;

2.2、關鍵點定位

以上方法檢測到的極值點是離散空間的極值點，以下通過擬合三維二次函式來精確確定關鍵點的位置和尺度，同時去除低對比度的關鍵點和不穩定的邊緣響應點(因為DoG運算元會產生較強的邊緣響應)，以增強匹配穩定性、提高抗噪聲能力。

2.2.1、關鍵點精確定位

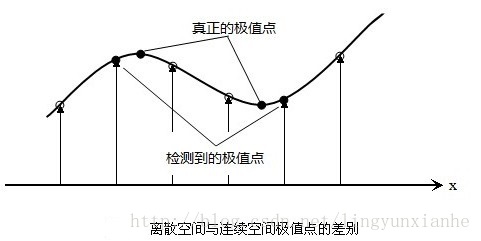
離散空間的極值點並不是真正的極值點，下圖顯示了二維函式離散空間得到的極值點與連續空間極值點的差別。利用已知的離散空間點插值得到的連續空間極值點的方法叫做子畫素插值。

為了提高關鍵點的穩定性，需要對尺度空間DoG函式進行曲線插值。利用DoG函式在尺度空間的Taylor展開式(插值函式)為：

上面算式的矩陣表示如下：

 其中，X求導並讓方程等於零，可以得到極值點的偏移量為：

對應極值點，方程的值為：

其中, X^代表相對插值中心的偏移量，當它在任一維度上的偏移量大於0.5時（即x或y或 σ），意味著插值中心已經偏移到它的鄰近點上，所以必須改變當前關鍵點的位置。同時在新的位置上反覆插值直到收斂；也有可能超出所設定的迭代次數或者超出影象邊界的範圍，此時這樣的點應該刪除，在Lowe中進行了5次迭代。另外，過小的點易受噪聲的干擾而變得不穩定，所以將 小於某個經驗值(Lowe論文中使用0.03，Rob Hess等人實現時使用0.04/S)的極值點刪除。同時，在此過程中獲取特徵點的精確位置(原位置加上擬合的偏移量)以及尺度(σ)。

2.2.2、消除邊緣響應

       一個定義不好的高斯差分運算元的極值在橫跨邊緣的地方有較大的主曲率，而在垂直邊緣的方向有較小的主曲率。DOG運算元會產生較強的邊緣響應，需要剔除不穩定的邊緣響應點。獲取特徵點處的Hessian矩陣，主曲率通過一個2x2 的Hessian矩陣H求出（D的主曲率和H的特徵值成正比）：

      

假設H的特徵值為α和β（α、β代表x和y方向的梯度）且α>β。令α=rβ則有：

其中Tr(H)求取H的對角元素和；Det(H)為求H的行列式值。

則公式(r+1)^2/r的值在兩個特徵值相等時最小，隨著的增大而增大。值越大，說明兩個特徵值的比值越大，即在某一個方向的梯度值越大，而在另一個方向的梯度值越小，而邊緣恰恰就是這種情況。所以為了剔除邊緣響應點，需要讓該比值小於一定的閾值，因此，為了檢測主曲率是否在某域值r下，只需檢測:

論文建議r=10,OpenCv也採用r=10

2.2.3、精確定位中的泰勒插值原始碼分析

while (i < SIFT_MAX_INTERP_STEPS)//SIFT_MAX_INTERP_STEPS=5為最大迭代次數，避免長時迭代

{

interp_step(dog_pyr, octv, intvl, r, c, &xi, &xr, &xc);// 泰勒展開擬合，xi,xr,xc依次為x、y、σ方向偏移量,

if (ABS(xi) < 0.5 && ABS(xr) < 0.5 && ABS(xc) < 0.5)//如果當前偏移量絕對值中的每個值均小於0.5，退出迭代

break;

c += cvRound(xc);//計算行座標，cvRound 為四捨五入。

r += cvRound(xr);

intvl += cvRound(xi);

if (intvl < 1 ||//不在計算的影象層中

intvl > intvls ||//高斯差分每組的層數為intvls

c < SIFT_IMG_BORDER ||//靠近影象邊緣5個畫素的區域不做檢測，SIFT_IMG_BORDER=5,

r < SIFT_IMG_BORDER ||

c >= dog_pyr[octv][0]->width - SIFT_IMG_BORDER ||//靠近影象邊緣5個畫素的區域不做檢測

r >= dog_pyr[octv][0]->height - SIFT_IMG_BORDER)

{

return NULL;

}

i++;//迭代計數

}

3、關鍵點方向分配

為了使描述符具有旋轉不變性，需要利用影象的區域性特徵為給每一個關鍵點分配一個基準方向。使用影象梯度的方法求取區域性結構的穩定方向。

3.1、特徵點的梯度

3.1.1、梯度的計算

對於在DOG金字塔中檢測出的關鍵點點，採集其所在高斯金字塔影象3σ領域視窗內畫素的梯度和方向分佈特徵。梯度的模值和方向如下：

L為關鍵點所在的尺度空間值，按Lowe的建議，梯度的模值m(x,y)按 σ=1.5σ_oct 的高斯分佈加成，按尺度取樣的3σ原則，領域視窗半徑為 3x1.5σ_oct。

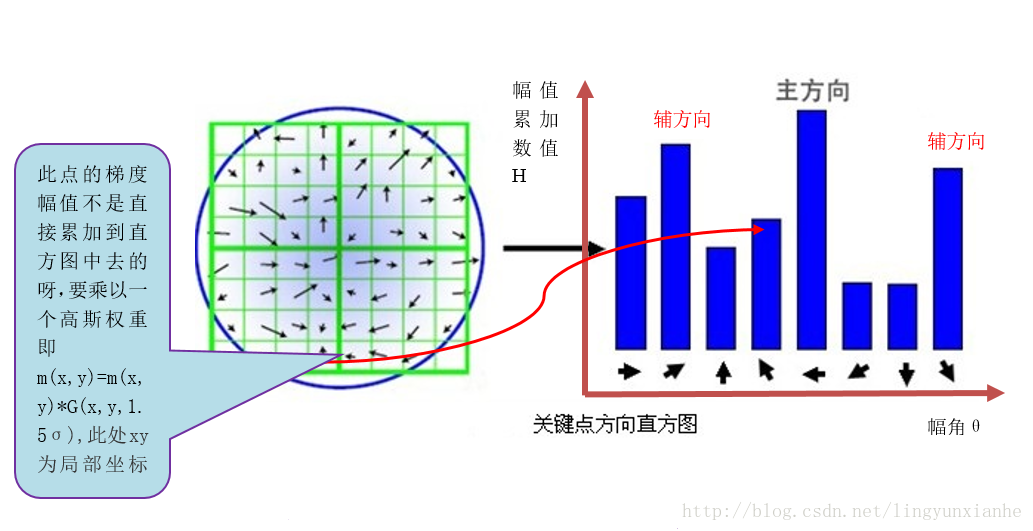
3.1.1、梯度直方圖

在完成關鍵點的梯度計算後，使用直方圖統計領域內畫素的梯度和方向。梯度直方圖將0~360度的方向範圍分為36個柱(bins)，其中每柱10度。如圖5.1所示，直方圖的峰值方向代表了關鍵點的主方向，(為簡化，圖中只畫了八個方向的直方圖)。

3.2、特徵點主方向的確定

      方向直方圖的峰值則代表了該特徵點處鄰域梯度的方向，以直方圖中最大值作為該關鍵點的主方向。為了增強匹配的魯棒性，只保留峰值大於主方向峰值80％的方向作為該關鍵點的輔方向。因此，對於同一梯度值的多個峰值的關鍵點位置，在相同位置和尺度將會有多個關鍵點被建立但方向不同。僅有15％的關鍵點被賦予多個方向，但可以明顯的提高關鍵點匹配的穩定性。實際程式設計實現中，就是把該關鍵點複製成多份關鍵點，並將方向值分別賦給這些複製後的關鍵點，並且，離散的梯度方向直方圖要進行插值擬合處理，來求得更精確的方向角度值。

3.2.1、梯度影象的平滑處理

      為了防止某個梯度方向角度因受到噪聲的干擾而突變，我們還需要對梯度方向直方圖進行平滑處理。Opencv  所使用的平滑公式為：

      

其中i∈[0,35],h 和H 分別表示平滑前和平滑後的直方圖。由於角度是迴圈的，即00=3600，如果出現h(j)，j超出了(0,…,35)的範圍，那麼可以通過圓周迴圈的方法找到它所對應的、在00=3600之間的值，如h(-1) = h(35)。

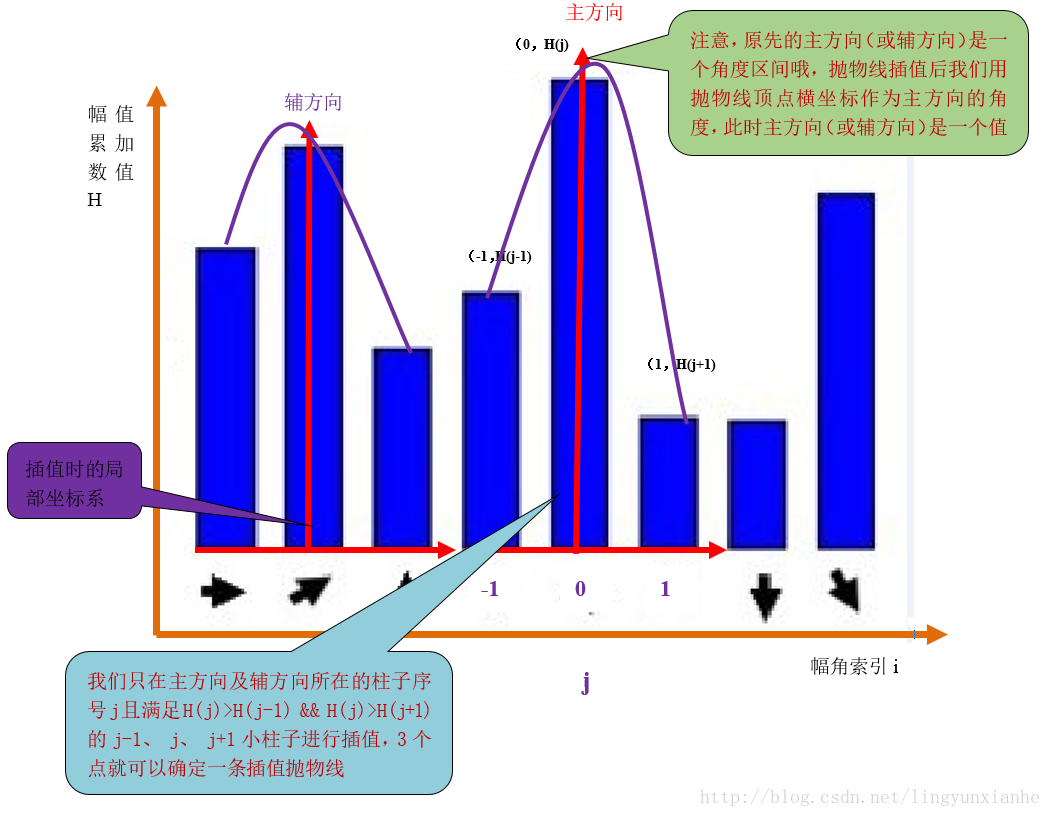
3.2.2、梯度直方圖拋物線插值

假設我們在第i個小柱子要找一個精確的方向，那麼由上面分析知道：

設插值拋物線方程為h(t)=at2+bt+c,其中a、b、c為拋物線的係數，t為自變數，t∈[-1,1],此拋物線求導並令它等於0。

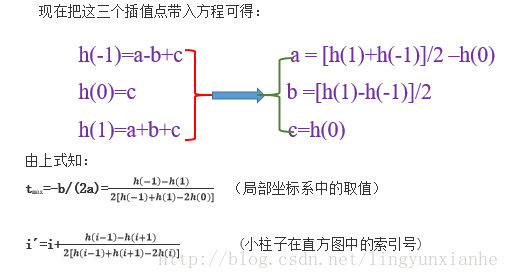
即h(t)´=0 得tmax=-b/(2a)

現在把這三個插值點帶入方程可得：

3.2.3、拋物線插值原始碼分析

#define interp_hist_peak( l, c, r ) ( 0.5 * ((l)-(r)) / ((l) - 2.0*(c) + (r)) )//插值計算式，l為左側柱子值，r為左側柱子值

static void add_good_ori_features(CvSeq* features, double* hist, int n,

double mag_thr, struct feature* feat)//精確主方向及輔方向

{

struct feature* new_feat;

double bin, PI2 = CV_PI * 2.0;//CV_PI=pi

int l, r, i;

for (i = 0; i < n; i++)// 直方圖有n=36個小柱子

{

l = (i == 0) ? n - 1 : i - 1;//把小柱子看成是迴圈的，角度的取值為0-360即一個圓周

r = (i + 1) % n;

//只對小柱子的值大於等於主峰80%且此小柱子比左右兩邊小柱子都高的柱子進行拋物線插值

if (hist[i] > hist[l] && hist[i] > hist[r] && hist[i] >= mag_thr)// mag_thr為>=80%的最高峰值

{

bin = i + interp_hist_peak(hist[l], hist[i], hist[r]);//interp_hist_peak 插值函式

bin = (bin < 0) ? n + bin : (bin >= n) ? bin - n : bin;//角度取值約束在0-360之間，且是連續迴圈的

new_feat = clone_feature(feat);//幅值特徵點

new_feat->ori = ((PI2 * bin) / n) - CV_PI;//？

cvSeqPush(features, new_feat);

free(new_feat);

}

 至此，影象的關鍵點已檢測完畢，每個關鍵點有三個資訊：位置、所處尺度、方向。由此可以確定一個SIFT特徵區域。

4、特徵點描述符

     通過以上步驟，對於每一個關鍵點，擁有三個資訊：位置、尺度以及方向。接下來就是為每個關鍵點建立一個描述符，使其不隨各種變化而改變，比如光照變化、視角變化等等。並且描述符應該有較高的獨特性，以便於提高特徵點正確匹配的概率。 

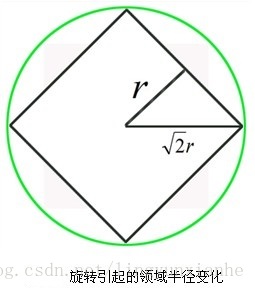
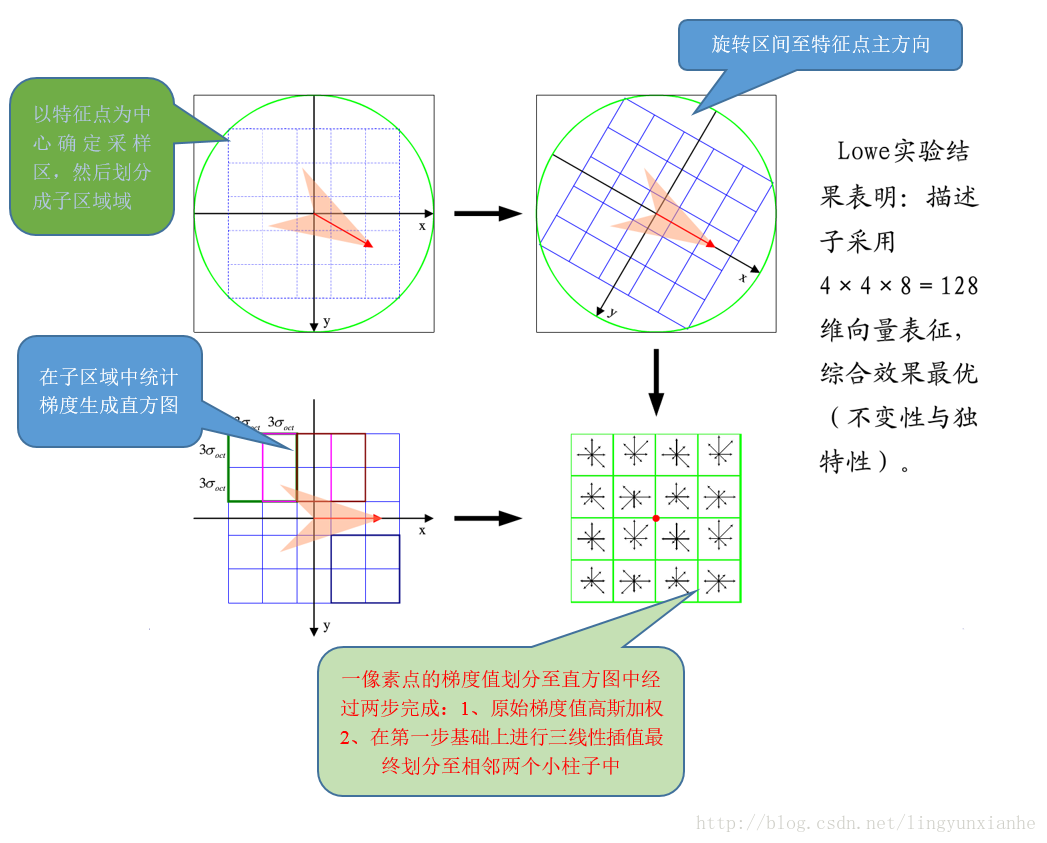
4.1、特徵的生成過程4.1.1、確定計算描述子所需的區域

       將關鍵點附近的區域劃分為d*d(Lowe建議d=4)個子區域，每個子區域作為一個種子點，每個種子點有8個方向。考慮到實際計算時，需要採用三線性插值，所需影象視窗邊長為3x3xσ_oct x(d+1)  。在考慮到旋轉因素(方便下一步將座標軸旋轉到關鍵點的方向)，如下圖6.1所示，實際計算所需的影象區域半徑為：

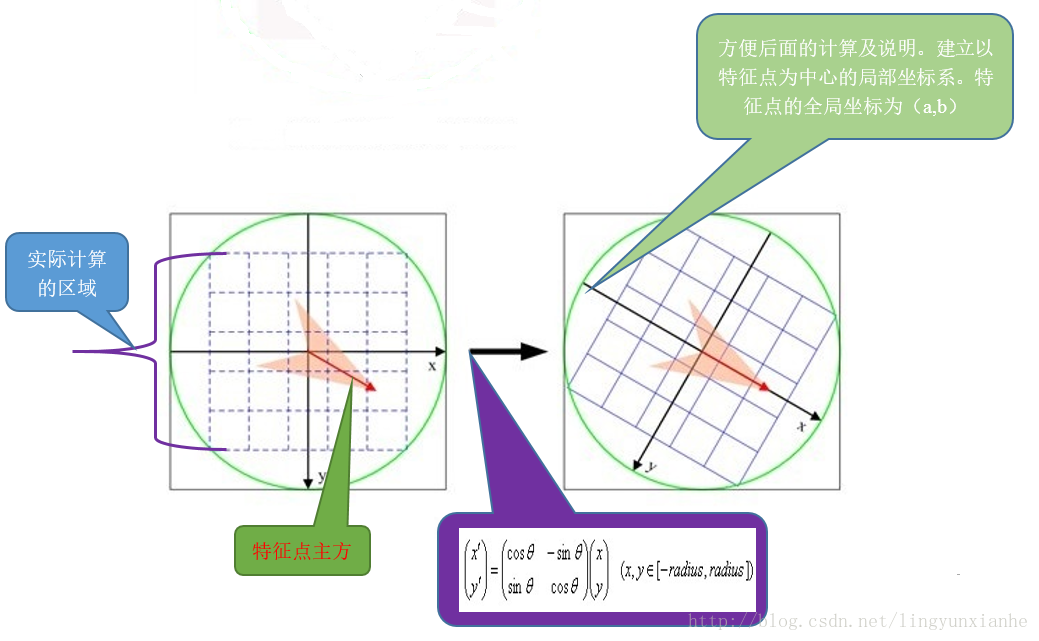
4.1.2、座標軸旋轉至主方向

將座標軸旋轉為關鍵點的方向，以確保旋轉不變性。

4.1.3、梯度直方圖的生成

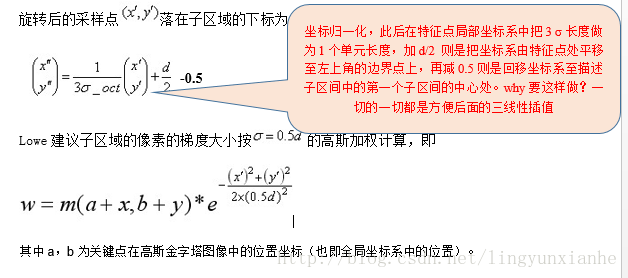
      將鄰域內的取樣點分配到對應的子區域內，將子區域內的梯度值分配到8個方向上，計算其權值。

旋轉後的取樣點 落在子區域的下標為

4.1.4、三線性插值

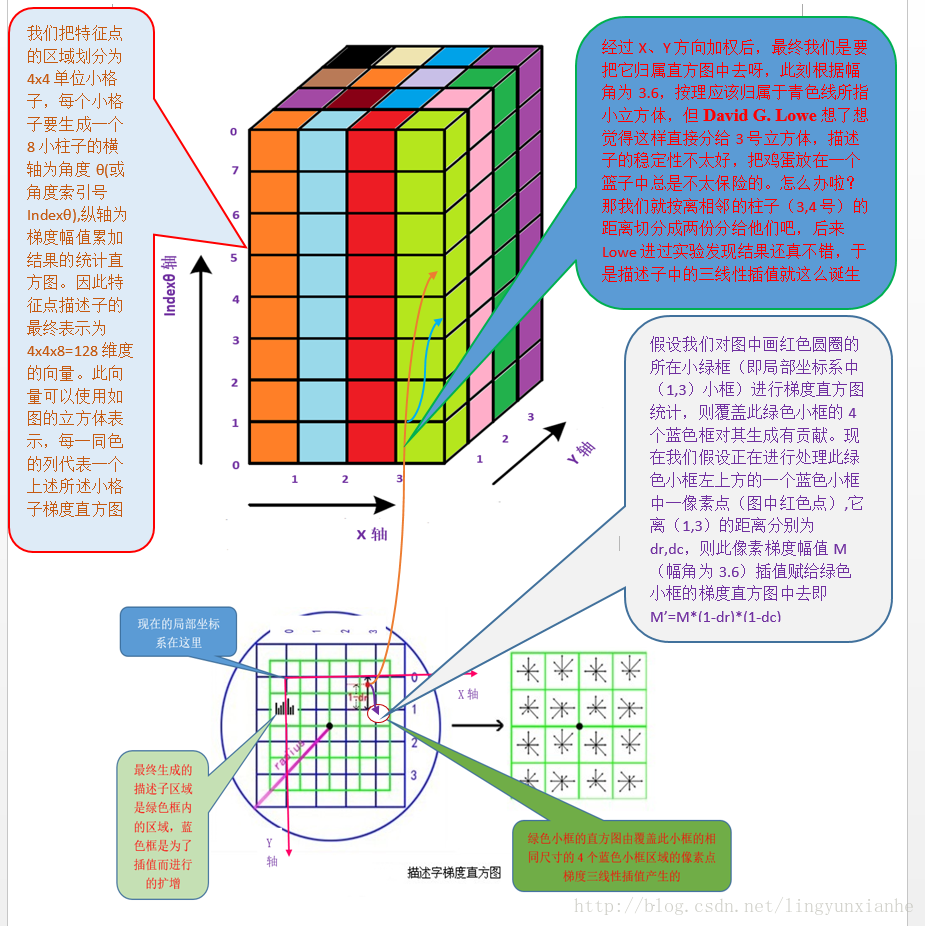
    插值計算每個種子點八個方向的梯度。

       取樣點在子區域中的下標(x'',y'')                              (圖中藍色視窗內紅色點)線性插值，計算其對每個種子點的貢獻。如圖中的紅色點，落在第0行和第1行之間，對這兩行都有貢獻。對第0行第3列種子點的貢獻因子為dr，對第1行第3列的貢獻因子為1-dr，同理，對鄰近兩列的貢獻因子為dc和1-dc，對鄰近兩個方向的貢獻因子為do和1-do。則最終累加在每個方向上的梯度大小為：

其中k，m，n為0（畫素點超出了對要插值區間的四個鄰近子區間所在範圍）或為1（畫素點處在對要插值區間的四個鄰近子區間之一所在範圍）。

4.1.5、特徵描述子

  如上統計的4*4*8=128個梯度資訊即為該關鍵點的特徵向量。

特徵向量形成後，為了去除光照變化的影響，需要對它們進行歸一化處理，對於影象灰度值整體漂移，影象各點的梯度是鄰域畫素相減得到，所以也能去除。得到的描述子向量為H=(h1,h2,.......,h128)，歸一化後的特徵向量為L=(L1,L2,......,L128)，則

      

4.1.6、描述子的門限化

        非線性光照，相機飽和度變化對造成某些方向的梯度值過大，而對方向的影響微弱。因此設定門限值(向量歸一化後，一般取0.2)截斷較大的梯度值(大於0.2的則就令它等於0.2，小於0.2的則保持不變)。然後再進行一次歸一化處理，提高特徵的鑑別性。

4.2、描述子相關分析

     用一組圖來概括描述子的生成過程

4.2.1、描述子生成總括

   

4.2.3、描述子三線性插值原始碼分析

static void interp_hist_entry(double*** hist, double rbin, double cbin,

double obin, double mag, int d, int n)

{

double d_r, d_c, d_o, v_r, v_c, v_o;

double** row, *h;

int r0, c0, o0, rb, cb, ob, r, c, o;

r0 = cvFloor(rbin);//向下取整

c0 = cvFloor(cbin);

o0 = cvFloor(obin);

d_r = rbin - r0;//小數餘項

d_c = cbin - c0;

d_o = obin - o0;

for (r = 0; r <= 1; r++)//沿著行方向不超過1個單位長度

{

rb = r0 + r;

if (rb >= 0 && rb < d)//如果此刻還在真正的描述子區間內

{

v_r = mag * ((r == 0) ? 1.0 - d_r : d_r);//d_r = rbin - r0;

row = hist[rb];

for (c = 0; c <= 1; c++)//沿著行方向不超過1個單位長度

{

cb = c0 + c;

if (cb >= 0 && cb < d)

{

v_c = v_r * ((c == 0) ? 1.0 - d_c : d_c);

h = row[cb];

for (o = 0; o <= 1; o++)//沿著直方圖方向不超過1個單位角度

{

ob = (o0 + o) % n；//n=8，8個小柱子

v_o = v_c * ((o == 0) ? 1.0 - d_o : d_o);

h[ob] += v_o;

}

}

}

}

      通過上面的1至4個大步驟就可以完成SIFT演算法對影象特徵點的提取。至此SIFT演算法完結。影象特徵提取是影象匹配的基礎，經過此演算法提取出來的特徵點用於後續的影象特徵匹配和特徵識別中，關於影象特徵匹配相關內容將在後續講解。

參考文獻

1、sift演算法詳解及應用（課件）。（本文件簡明扼要的簡述了SIFT演算法和影象匹配以及匹配修正。圖文並茂，一覽全貌）

2、SIFT演算法詳解（sift操作過程理論通俗，尤其是高階泰勒展開式及高階導數分析的很好，對理解亞畫素定位擬閤中的影象具體程式設計操作很有用）

3、SIFT特徵分析與原始碼解讀（1模擬金字塔的過程解釋的很詳細，帶有動畫模擬；2 在尋找特徵點進行亞畫素定位擬閤中的影象很形象）

4、【OpenCV】SIFT原理與原始碼分析：關鍵點描述（對關鍵點描述子區域的取捨講解的很詳細）

5、【OpenCV】SIFT原理與原始碼分析（對sift 演算法採用分部分敘述且帶有原始碼分析說明）

6、opencv2.4.9sift原始碼分析(1趙春江的這篇文章是我目前看到分析sift演算法比較全面的；2尤其給出了使用三維直方圖來分析三線性插值，對理解描述子的生成作用很大；3 給出了原始碼分析和演示結果）

（1演算法中尋找主方向使用的拋物線插值擬合方法；2 描述子三次插值）

8、RobHess的SIFT原始碼分析：綜述(各個子程式詳解及分析很細緻，一概全貌）

9、特徵點檢測學習_1(sift演算法)（1這篇文章沒有太多理論分析，但結合QT和OpenCV做出了生動的sift演算法匹配演示，有圖很直觀生動呀，用程式配圖一目瞭然；2 簡述對robhess 的c版本sift程式碼在c++中的使用注意問題 ）

 10、OpenCV 中c版本sift原始碼網址

11、【特徵匹配】SIFT原理與C原始碼剖析（這個也不錯，圖文並茂，還帶有  原始碼分析，總體來說是以程式帶動問題分析）

12、插值與擬合（對多項式及其插值講解還不錯）

http://wenku.baidu.com/link?url=wWcqLrpokQrjZZKzFbuJ4QDbZXZkMByCu-KaVKrSyGD6fh9Bpk1kZOPitpkFpNBw_no8UoyWY2DGQg9I7aL_tO3oi7z5mUK7cN8Sca6dX-O

13、線性插值與拋物線插值（對這兩種插值講解的很詳細，是目前發現最 好的一版

14、奇異值分解（對奇異值怎麼來的講解比較細緻）