JointFlow: Temporal Flow Fields for Multi Person Pose Tracking
摘要
- 多目標姿態跟蹤
- 使用了時間流場(Temporal Flow Fields)
- 基於相鄰兩幀
和
- 時間網路的通用設計,使得其可以和多種人體姿態估計的空間網路搭配,這裡指時間網路主要處理track問題,而空間網路主要針對detect問題
- 使用CNN提取相鄰兩幀的影象feature 和 pose feature
- 時間網路根據這兩種feature 推理出Temporal Flow Fields(TFF), TFF是一個向量場(感覺和光流差不多),蘊含了pose從幀
到幀
的運動方向
- 根據這種新穎的表達TFF,可以設計出一種檢測pose之間相似性的度量
- 而設計出的相似性,可以作為二分圖優化問題的邊權重,用於多姿態跟蹤問題的求解
- 文章表明,這些TFF可以通過一個相對較小的CNN網路(跟蹤領域新穎的星羅網路(Siamese Network)學習,同時實現最先進的多人姿態跟蹤結果
介紹
FIRA(Rohit Girdhar, Georgia Gkioxari, Lorenzo Torresani, Manohar Paluri, and Du Tran. Detect-and-track: Efficient pose estimation in videos. CVPR, 2018.)
Pose Flow (Yuliang Xiu, Jiefeng Li, Haoyu Wang, Yinghong Fang, and Cewu Lu. Pose Flow:
Efficient online pose tracking. BMVC, 2018.)
這兩種state-of-the-art 方法使用現成的多人姿態估計方法檢測姿態,然後接一個額外的後處理用於連結不同幀的相同目標。
現有的兩種時間上關聯目標的方法:
- 線上的方法,來一幀處理一幀,根據當前幀和上一幀的相似性進行目標關聯,代表作有,MSRA,
- 離線的方法,先把整個視訊的pose都檢測出來,然後執行pose track方法使得關聯結果保持全域性一致性,代表作有:PoseTrack,
上述的關聯方法都依賴於一些相似性的度量,同時這相似性度量的選擇非常重要,相似性度量和track方法必須相匹配,度量要要滿足track方法對相似性的表現要求,現有的相似性度量有以下方法:
- PCKh,在pose估計的資料集中有定義,代表作有 FIRA(Rohit Girdhar, Georgia Gkioxari, Lorenzo Torresani, Manohar Paluri, and Du Tran. Detect-and-track: Efficient pose estimation in videos. CVPR, 2018.)
- OKS(Object Keypoint Similarity)代表作有,MSRA
- IOU FIRA
- Optical flow ArtTrack: Articulated Multi-person Tracking in the Wild, PoseTrack, Pose Flow: Efficient online pose tracking.
一方面基於位置的度量如PCKh、OKS或IoU,假定姿勢隨時間的推移而平穩變化,因此,在大型相機或身體姿勢運動和由於相機變焦引起的比例變化的情況下,會遇到困難。
另一方面,基於外觀的相似性度量或光流資訊不能處理由於人的遮擋或截斷、運動模糊等造成的外觀變化。
離線方法試圖通過加強長期時間一致性來應對這些挑戰。這通常是通過使用複雜的時空圖來構造問題來實現的(ArtTrack: Articulated Multi-person Tracking in the Wild, PoseTrack),這導致了很高的推理時間,因此,這些方法在許多應用中是不可行的。
這文章中,筆者指出上述的相似性度量都並非是專為這個問題設計的(task-agnostic)
提出使用(task-spacific)TFF 來輔助定義相鄰幀之間相關性的度量(時間域上的)
這個TFF受啟發於PAF,PAF是用於單幀內關節之間相關性度量的(空間域上的)
通過TFF定義相關度,構成二分圖,利用貪婪的匹配演算法求解track問題
方法
首先是網路推理部分:

- 兩幀圖片經過Siamese網路提取特徵
- 特徵一方面分別經過Spatial Inference得到各幀的pose以及PAF
- 一方面兩幀feature結合送給Temporal Model 估計TFF
然後是邏輯推理部分:
- 首先在單幀內使用PAF方法連結不同的關節點得到不同的人個體
- 然後是不同幀的人關聯,利用TFF構建二分圖
- 使用貪婪演算法求解二分圖匹配,把上一幀的標籤 pass 到當前幀(文章好像沒有提如何匹配,但是下面的根據TFF最後得到的優化目標是可以通過匈牙利演算法或者貪婪匹配演算法(參考MSRA)求得的)
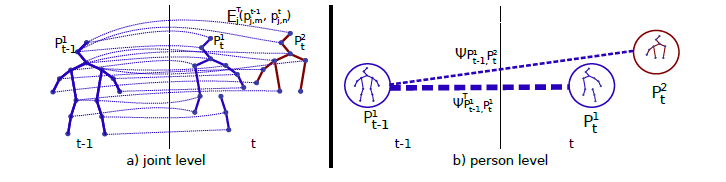
利用TFF構建二分圖
如上圖右邊所示,定義每個人的pose 為關鍵點集合,總共J個關鍵點,
是關鍵點
的座標
幀中共有
個目標,構成集合
優化的目標定義為:
s.t. and
其中
是二值變數,1表示這兩幀中的這兩個目標相關,由匹配演算法得到
是這兩幀中這兩個目標的相關度,定義是根據關節相關度的,如下
定義的是關節是否被檢測到,如果
兩個關節都被檢測到,則
定義的是兩個關節的相關度,定義如下:
如果兩個關節的位置特別相近就定義為1,否則就根據TFF定義:
這裡是一個積分,積分變數為,
是點座標
是一個向量,定義為兩個關節點之間連線上所有點p的,在該關節的TFF中,向量T(p)的和:
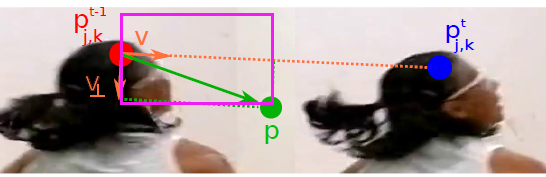
為了讓網路可以學習到TFF的分佈,即的分佈,訓練的時候定義如下的gt,對於每一點p:
,這裡考慮到所有的目標(場景中的K個人)對該點TFF的影響,求均值,有可能不同的人的關節點的
有重合,這時就求均值。也可以看成,每個人都產生一個關於關節J的TFF的向量場,而關節J的TFF向量場,是這些各個目標向量場的均值。(CNN設計時,輸出的TFF通道數和關節數量相等,而和圖片中人的數量無關,對於每一個關節,CNN推理一個TFF向量場,總共J個TFF向量場,每一個向量場要考慮所有的目標)
如果該點p在上圖中,由定義的紫色框內,則等於
,否則等於0
