Triplet Loss入門

Face verification vs. face recogntion

Verification

• Input image, name/ID
• Output whether the input image is that of the claimed person.

Recognition

• Has a database of K peosons(or not recognized)

Relations

We can use a face verification system to make a face recognition system. The accuracy of the verification system has to be high (around 99.9% or more) to be use accurately within a recognition system because the recognition system accuracy will be less than the verification system given K persons.

One Shot Learning

• One of the face recognition challenges is to solve one shot learning problem.
• One Shot Learning: A recognition system is able to recognize a person, learning from one image.
• Historically deep learning doesn’t work well with a small number of data.
  Instead to make this work, we will learn a similarity function:
  $d$
  ( i m g 1 , i m g
  2 ) d( img1, img2 ) = degree of difference between images.
  We want d result to be low in case of the same faces.
  We use $\tau$ as a threshold for d:
  If $d( img1, img2 ) <= \tau$ Then the faces are the same.
• Similarity function helps us solving the one shot learning. Also its robust to new inputs.

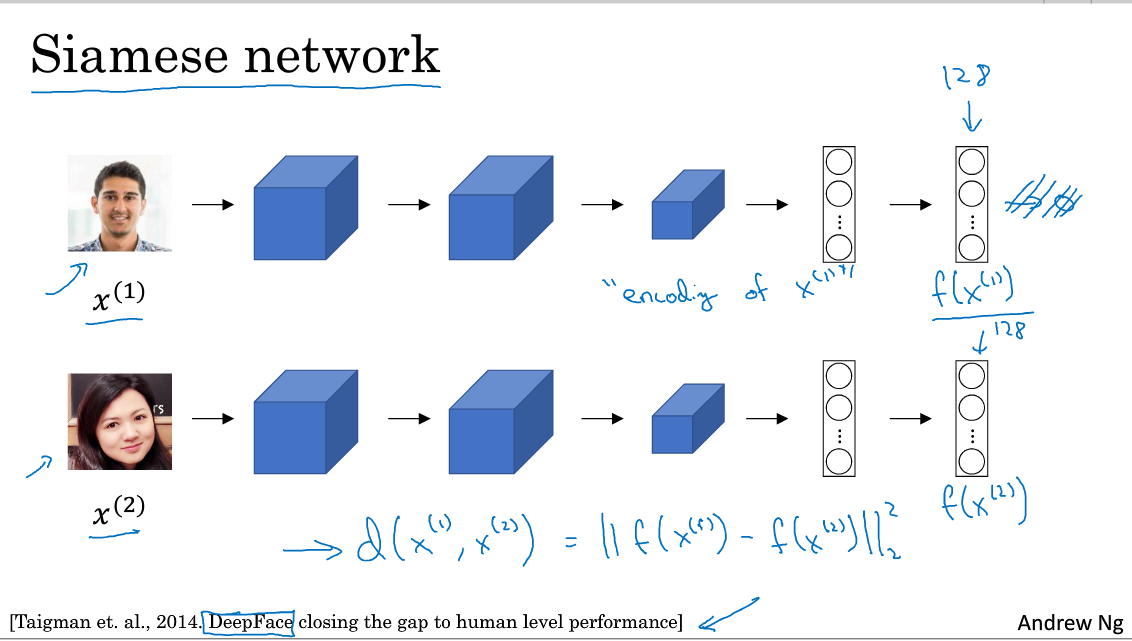
Siamese Network

• We will implement the similarity function using a type of NNs called Siamease Network in which we can pass multiple inputs to the two or more networks with the same architecture and parameters.
• The loss function will be $d(x^1, x^2) = || f(x^1) - f(x^2) ||^2$
  

Triplet Loss

Firstly

• Triplet Loss is one of the loss functions we can use to solve the similarity distance in a Siamese network.
• $||f(A) - f(P)||^2 <= ||f(A) - f(N)||^2$
• $||f(A) - f(P)||^2 - ||f(A) - f(N)||^2 <= 0$
• $||f(A) - f(P)||^2 - ||f(A) - f(N)||^2 <= -\alpha$ to make sure the NN won’t get an output if zero

Secondly

• Given 3 images (A, P, N)
• $L(A, P, N) = max (||f(A) - f(P)||^2 - ||f(A) - f(N)||^2 + alpha , 0)$
• $J = \sum(L(A[i], P[i], N[i]) , i) $for all triplets of images.

Thirdly

• During training if A, P, N are chosen randomly (Subjet to A and P are the same and A and N aren’t the same) then one of the problems this constrain is easily satisfied
• What we want to do is choose triplets that are hard to train on.

Offline triplet mining

1.最簡單的想法就是離線演算法，先找到B個triplets計算它們的loss然後再送進網路學習，但是這樣很低效，要遍歷整個網路。

Online triplet mining

1.對於一個有B個樣本的batch，我們最多可以產生 $B^3$個triplets。這裡面雖然有很多無效的（沒有兩個P，一個N），但是卻可以在一個batch中產生更多的triplets。
2.Batch hard strategy
找到每個anchor最hardest的P和N

• 計算一個2D距離矩陣然後將無效的設定為0，將有效的pair留下來（ $a\neq p,$ a和p有著相同的label），然後在修改後的矩陣計算每一行的最大值。
• 計算最小值N的時候不能將無效的設定為0（無效的是a和
  n有著相同的label）。

def batch_hard_triplet_loss(labels, embeddings, margin, squared=False):
    """Build the triplet loss over a batch of embeddings.

    For each anchor, we get the hardest positive and hardest negative to form a triplet.

    Args:
        labels: labels of the batch, of size (batch_size,)
        embeddings: tensor of shape (batch_size, embed_dim)
        margin: margin for triplet loss
        squared: Boolean. If true, output is the pairwise squared euclidean distance matrix.
                 If false, output is the pairwise euclidean distance matrix.

    Returns:
        triplet_loss: scalar tensor containing the triplet loss
    """
    # Get the pairwise distance matrix
    pairwise_dist = _pairwise_distances(embeddings, squared=squared)

    # For each anchor, get the hardest positive
    # First, we need to get a mask for every valid positive (they should have same label)
    mask_anchor_positive = _get_anchor_positive_triplet_mask(labels)
    mask_anchor_positive = tf.to_float(mask_anchor_positive)

    # We put to 0 any element where (a, p) is not valid (valid if a != p and label(a) == label(p))
    anchor_positive_dist = tf.multiply(mask_anchor_positive, pairwise_dist)

    # shape (batch_size, 1)
    hardest_positive_dist = tf.reduce_max(anchor_positive_dist, axis=1, keepdims=True)

    # For each anchor, get the hardest negative
    # First, we need to get a mask for every valid negative (they should have different labels)
    mask_anchor_negative = _get_anchor_negative_triplet_mask(labels)
    mask_anchor_negative = tf.to_float(mask_anchor_negative)

    # We add the maximum value in each row to the invalid negatives (label(a) == label(n))
    max_anchor_negative_dist = tf.reduce_max(pairwise_dist, axis=1, keepdims=True)
    anchor_negative_dist = pairwise_dist + max_anchor_negative_dist * (1.0 - mask_anchor_negative)

    # shape (batch_size,)
    hardest_negative_dist = tf.reduce_min(anchor_negative_dist, axis=1, keepdims=True)

    # Combine biggest d(a, p) and smallest d(a, n) into final triplet loss
    triplet_loss = tf.maximum(hardest_positive_dist - hardest_negative_dist + margin, 0.0)

    # Get final mean triplet loss
    triplet_loss = tf.reduce_mean(triplet_loss)

    return triplet_loss