歸併排序

一.概述

這裡歸併的含義將兩個或兩個以上的有序表組合成一個新有序表，本文講述二路歸併排序。

二、排序過程

1. 初始序列看成n個有序子序列，每個子序列長度為1
2. 兩兩合併，得到（n/2向下取整數）個長度為2或1的有序子序列
3. 再兩兩合併，重複直至得到一個長度為n的有序序列為止

二路歸併排序主旨是“分解”與“歸併”

分解：　　

　1.將一個數組分成兩個陣列，分別對兩個陣列進行排序。

　2.迴圈第一步，直到劃分出來的“小陣列”只包含一個元素，只有一個元素的陣列預設為已經排好序。
　
歸併：

　1.將兩個有序的數組合併到一個大的陣列中。

　2.從最小的只包含一個元素的陣列開始兩兩合併。此時，合併好的陣列也是有序的。
　

1.將兩個順序表合併成一個有序表

首先我們來看看兩個順序表是如何變成一個有序表的，實際上做法就是將兩個指標指向兩個陣列，然後進行比較，看那個指標指向的資料小，將小的資料插入新的數組裡，然後將這個指標加1.如圖所示。

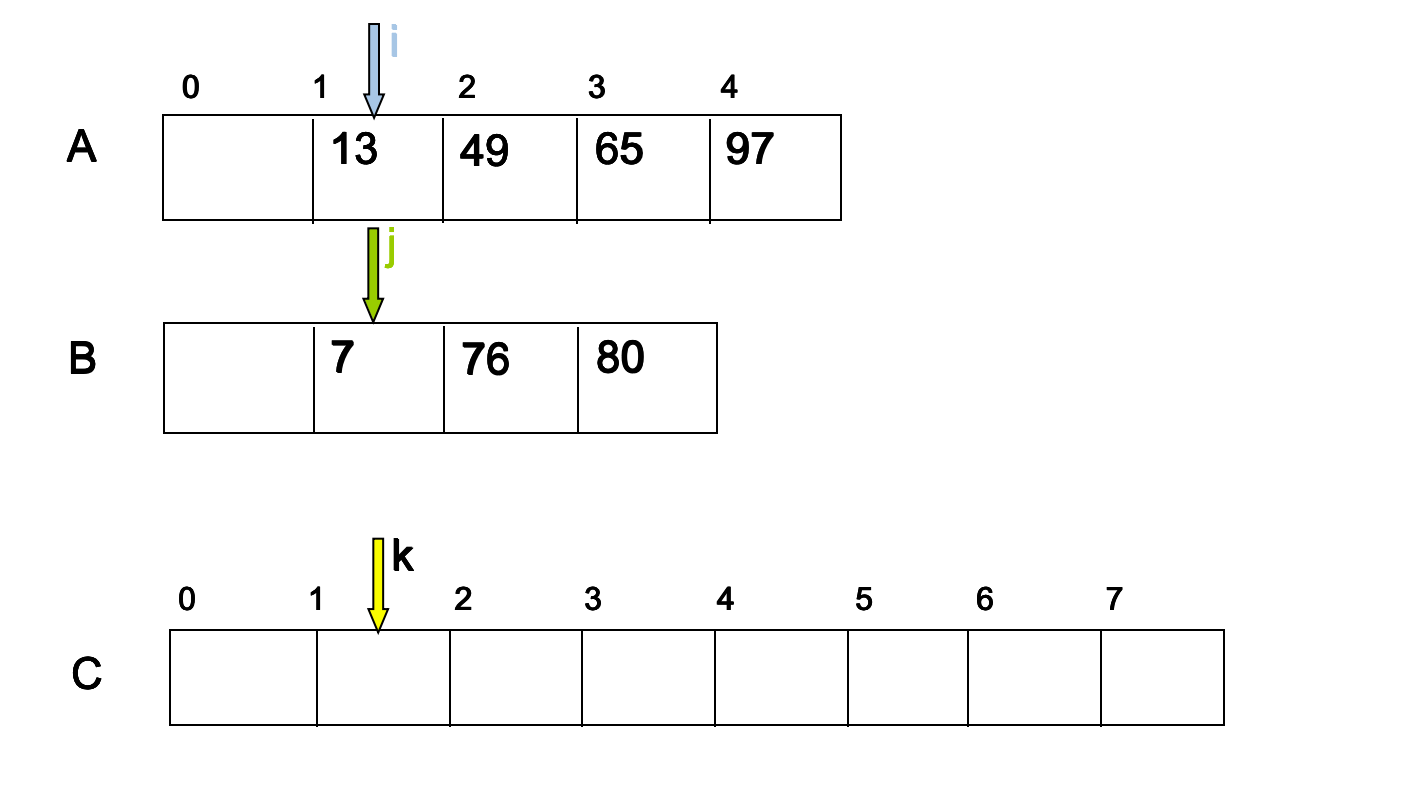
程式碼如下：

int [] mergeSort(int a[] , int b[],){
    int c[a.length + b.length] ;
    int i = 0; 
    int j = 0;
    int k = 0;
    while (i < a.length && j < b.length){
       if ( a[i] < b [j]){
          c[k ++] = a[i];
          i ++;
       }else{
 
         c[k ++] = b[j];
         j++;
       }  
   }
   while ( i < a.length ){
        c[k] = a [i];
        i ++;
        k ++;
   }
   while ( j <b .length ){
       c[k] = a [j];
       j ++;
       k ++;
   }
 return c;
}
 

2.過程

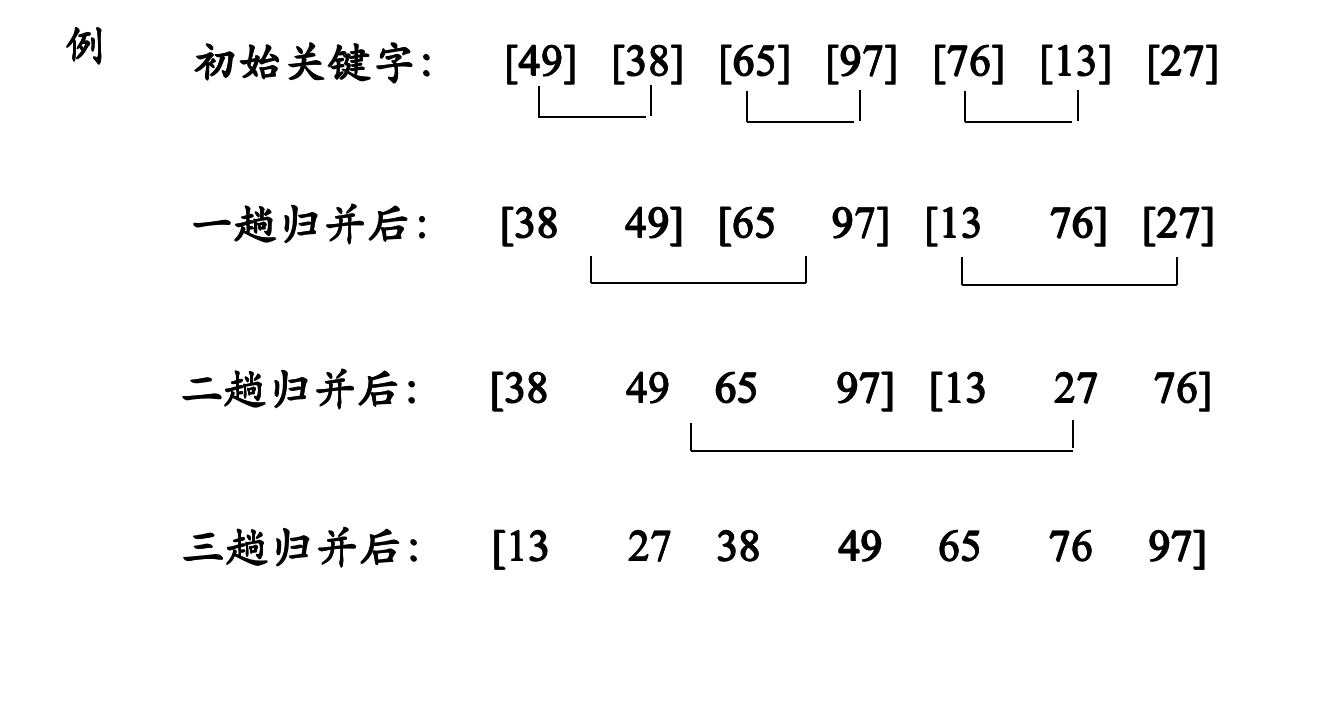
可以看出這個過程，每次兩兩進行比較的時候，都可以表示是兩個有序的陣列，變成一個有序陣列的過程。經過數次的變化，就好變成排序狀態的陣列。

三.演算法分析

時間效率：$O(nlog_2n) $
空間效率：\(O（n）\)
穩 定 性：穩定

四.完整程式碼

public class MergeSort {

    public static int[] sort(int[] nums, int low, int high) {
        int mid = (low + high) / 2;
        if (low < high) {
            // 左邊
            sort(nums, low, mid);
            // 右邊
            sort(nums, mid + 1, high);
            // 左右歸併
            merge(nums, low, mid, high);

        }
        return nums;
    }

    public static void merge(int[] nums, int low, int mid, int high) {
        int[] temp = new int[high - low + 1];
        int i = low;// 左指標
        int j = mid + 1;// 右指標
        int k = 0;

        // 把較小的數先移到新陣列中
        while (i <= mid && j <= high) {
            if (nums[i] < nums[j]) {
                temp[k++] = nums[i++];

            } else {
                temp[k++] = nums[j++];

            }

        }
        // 把左邊剩餘的數移入陣列
        while (i <= mid) {
            temp[k++] = nums[i++];

        }

        // 把右邊邊剩餘的數移入陣列
        while (j <= high) {
            temp[k++] = nums[j++];

        }

        // 把新陣列中的數覆蓋nums陣列
        for (int k2 = 0; k2 < temp.length; k2++) {
            nums[k2 + low] = temp[k2];

        }

    }

}
 

參考 ：
https://www.cnblogs.com/horizonice/p/4102553.html
《資料結構》 嚴蔚敏
《演算法導論》2.1章節