標籤（空格分隔）： 神經網路

0.回顧

cs231n （一）影象分類識別講了KNN
cs231n （二）講了線性分類器：SVM和SoftMax
cs231n （三）優化問題及方法
cs231n （四）反向傳播
cs231n （五）神經網路 part 1:構建架構
cs231n （六）神經網路 part 2:傳入資料和損失
cs231n （七）神經網路 part 3 : 學習和評估
cs231n （八）神經網路總結：最小網路案例研究

1. 引言

經過一系列的學習終於抵達了傳說中的卷積神經網路，他和一般的網路很類似，前面學過的東西這裡全都能用上，那麼有什麼不同呢？

ConvNet結構假設輸入是影象，這就允許我們將某些屬性編碼到體系結構中，來吧，一般究竟哈？~~~emmmm

2. 總體概述

總體結構就是：輸入向量————>隱含層非線性變換————>輸出

對於前面講過的，CIFAR-10資料是32x32x3=3072（權重數）， 如果影象很大呢，比如一般影象的尺寸都達到了1000x1000x3 = 3000000（權重），這時候：

計算機說：我不幹了，累死我算了
卷積網路中的神經元是三維排列的，卷積只與前一層的部分連線，那麼對於DIFAR資料最後一層應該是1x1x10。

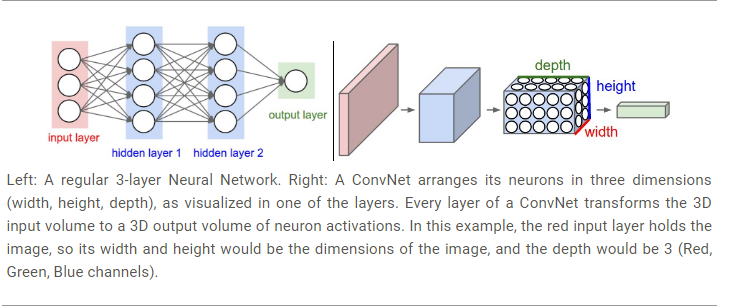
左邊：三層神經網路 右邊：卷積神經網路

卷積神經網路由層組成， 每層都有相應的API，用一些可導函式把輸入的3D資料轉換為輸出的3D資料。

3. 構建卷積網路的每個層

主要由三層組成：卷積——————池化——————全連線層！
比如CIFAR資料的話：

輸入層-————卷積層-————ReLU層（尺寸不變-———池化層-———全連線層
32x32x3————32x32x12——————32x32x12————————16x16x12————————1x1x10

• 輸入資料變為——————輸出資料
• CNN由很多層一般包含上述幾種層
• 每層輸入是3D資料，然後使用可導函式把它變為3D輸出資料
• 有的層含引數，有的沒有（卷積層和全連線層有，ReLU層和池化層沒）
  

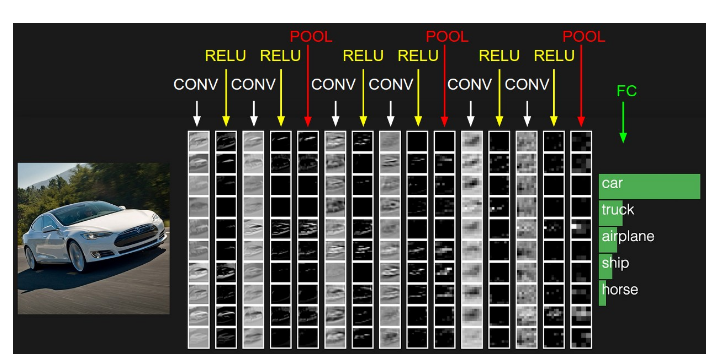
上圖中的結構是一個小型VGG網路

1. 卷積層

這層是核心層，主要是由一些濾波器構成，現在使用一套濾波器（比如12個）， 每層都會產生一個圖資料，然後疊加就是此層的輸出。

**例如：**輸入資料體尺寸[32x32x3]（比如CIFAR-10的RGB影象），卷積核大小是5x5，那麼卷積層中的每個神經元會有輸入資料體中[5x5x3]區域的權重，共5x5x3=75個權重（還要加一個偏差引數）。注意這個連線在深度維度上的大小必須為3，和輸入資料體的深度相同。

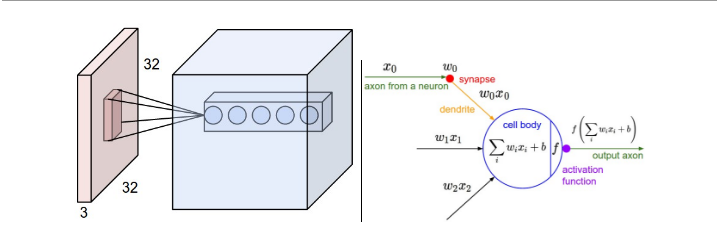
左邊：輸入資料，藍色是5個卷積核疊加形成的
右邊：計算的還是權重和輸入的內積。

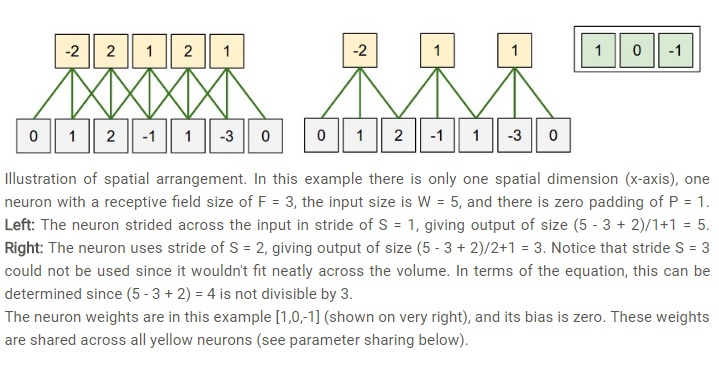
卷積層的輸出： 由深度（多深），步長（一次移動多遠），零填充（影象周圍加零）決定。

輸入資料尺寸：W 卷積核大小：F
步長:S 零填充數量：P

輸出的尺寸就是： (W-F+2P)/S + 1

P取多少為好？ 輸入與輸出相同尺寸時候滿足：P=(F-1)/2

引數共享：將深度維度上一個單獨的2維通道（就是一層）看做深度切片（depth slice）
比如：一個數據體尺寸為[55x55x96]的就有96個深度切片，每個尺寸為[55x55]，每個深度切片上的神經元都使用同樣的權重和偏差，

這樣卷積層輸出就有96個權重不同權重集，權重集合稱為濾波器（filter），這96個濾波器的尺寸都是[11x11x3]，每個都被55x55個神經元共享？

Krizhevsky等學習到的濾波器例子

具體Numpy例子

1. 位於(x,y)的深度列將會是X[x,y,:]
2. 位於深度d的切片應該是X[:,:,d]

假設輸入資料X的尺寸X.shape:(11,11,4)，不使用零填充，濾波器的尺寸：F=5，步長S=2，
輸出尺寸就是(11-5)/2+1=4

• V[0,0,0] = np.sum(X[:5,:5,:] * W0) + b0
• V[1,0,0] = np.sum(X[2:7,:5,:] * W0) + b0
• V[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0
• V[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0

小結： 總結一下卷積層的性質：

輸入資料體的尺寸為$ W_1\times H_1\times D_1$

4個超引數：
- 濾波器的數量K

• 濾波器的空間尺寸F
• 步長S
• 零填充數量P

輸出資料體的尺寸為$W_2\times H_2\times D_2 $，其中：$W_2=(W_1-F+2P)/S+1$

$H_2=(H_1-F+2P)/S+1$ （寬度和高度的計算方法相同）
$D_2=K$

1. 由於引數共享，每個濾波器包含$F\cdot F\cdot D_1$個權重，卷積層一共有$F\cdot F\cdot D_1\cdot K$個權重和$K$個偏置。

2. 在輸出資料體中，第d個深度切片（空間尺寸是$W_2\times H_2$），用第d個濾波器和輸入資料進行有效卷積運算的結果（使用步長S），最後在加上第d個偏差。

對這些超引數，常見的設定: F=3，S=1，P=1
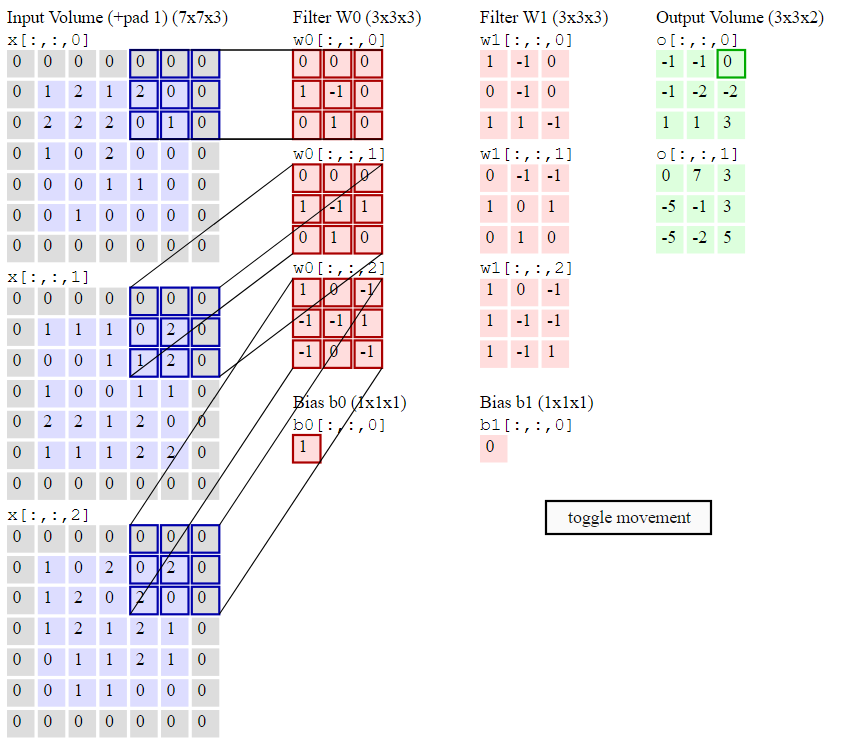
動態演示
輸入：$W_1=5,H_1=5,D_1=3$
卷積層引數: $K=2,F=3,S=2,P=1$
輸出: 是(5-3+2)/2+1=3

有2個濾波器，濾波器的尺寸是$3\cdot 3$，它們的步長是2.

動圖

1x1卷積，有意義: 因為如果我們處理的三維卷積，那麼比點積更有效。
擴張卷積讓濾波器中元素之間有間隙,在某維度上濾波器w的尺寸是3，
那麼計算輸入x的方式是：$w[0]*x[0] + w[1]*x[1] + w[2]*x[2]$，此時擴張為0.
那麼計算為, 如果擴張為1： $w[0]*x[0] + w[1]*x[2] + w[2]*x[4]$

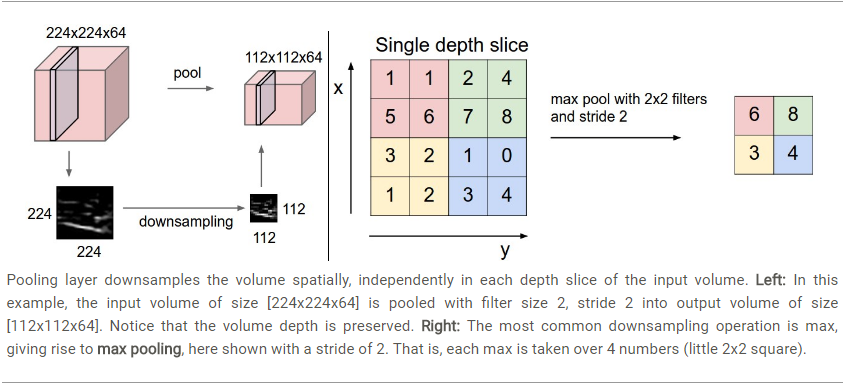
2. pooling池化層

一般會在連續的卷積層之間會週期性地插入一個池化層，可以降低資料體的維度，減少引數數量，能有效控制過擬合。

輸入資料體尺寸$W_1\cdot H_1\cdot D_1$
輸出資料體尺寸$W_2\cdot H_2\cdot D_2$，其中
$W_2=(W_1-F)/S+1$
$H_2=(H_1-F)/S+1$
$D_2=D_1$

在池化層中很少用零填充
常用引數：F = 3,S = 2； F = 2, S = 2.

有平均池化，有最大池化， L2池化等。

其實池化層的未來趨勢就是很少使用。

3. 歸一化層

4. 全連線層

神經元對前一層連線和前面學過的一般神經網路網路連線是一樣的。

5. 全連線層轉化為卷積層

• 卷積層和全連線層是可以相互轉化的
  如何轉轉化？
  一般hi全連線層轉化為卷積層更有用
  輸入：224x224x3
  經過一系列變換
  某層資料體：7x7x512

AlexNet中就是，使用5個池化層，每次尺寸下降一半，最終尺寸為224/2/2/2/2/2=7
AlexNet使用兩個尺寸為4096的全連線層，最後有1000個神經元的全連線層計算分數。

這3個全連線層中的一個轉化為卷積層的話：

• 對第一個連線區域 7x7x512 濾波器F=7，輸出就是1x1x4096
• 對於第二層，濾波器F=1, 輸出就是：1x1x4098
• 最後一個全連線層，F=1，輸出就是：1x1x1000

4. 如何構建卷積神經網路的結構

那麼如何組合這些，卷積層、池化層、全連線層、ReLU也算一層。

1. 層的排列方式

常見結構：**INPUT —> [[CONV -> RELU]*N -> POOL?]M -> [FC -> RELU]K —> FC
其中*N代表重複了N次，N<=3 且M>=0,K>=0,通常K<3，下面列出了常見的網路結構：

• INPUT -> FC,實現一個線性分類器，此處N = M = K = 0
• INPUT -> CONV -> RELU -> FC
• INPUT -> [CONV -> RELU -> POOL]*2 -> FC -> RELU -> FC
• INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL]*3 -> [FC -> RELU]*2 -> FC
• 上面的網路結構：在執行具有破壞性的池化前，多重的卷積可從輸入中學到更多複雜特徵

多個小濾波器卷積組合好於一個大濾波器
有點：輸出更多的特徵，且使用的特徵少。
缺點：在進行反向傳播時，中間的卷積層可能會導致佔用更多的記憶體。

2. 層的大小設定規律

**輸入層：**應該是可以被2整除很多次的，

3. 相關案例學習（LeNet/ AlexNet/ ZFNet/ GoogLeNet/ VGG）

4. 一些計算上的考慮

6. 其他資源