Adaptive Bilateral Filter for Sharpness Enhancement and Noise Removal 閱讀理解
ABF則是一直新的基於訓練的影象恢復演算法,它的範圍是處理適合數碼攝影的圖片,不考慮那些嚴重退化的影象。影象恢復演算法的廣泛應用的成功將取決於演算法開發的退化模型的一般程度,以及演算法的整體結構對偏離假設的退化模型的程度有多強。
ABF通過增加邊緣的斜率從而達到影象銳度增強的效果,並且不會出現過銳等問題,它不需要進行邊緣檢測,邊緣方向計算以及邊緣的橫截面進行計算。當然與USM這種通過增加高頻演算法進行影象增強演算法也不一樣。ABF中,邊緣的斜度變化是通過區域性直方圖分佈變化,這個區域性直方圖通過一個自適應寬度和偏移量的灰度值濾波器實現。ABF的引數是通過大量的樣本訓練得到。ABF可以同時繼續影象增強和去噪。
1 雙邊濾波如何實現保邊濾波的?
傳統的高斯濾波只考慮空間域進行平滑,離中心點越近權重越大,反之越小。這種低通濾波會丟失很多高頻資訊,因此人們提出了雙邊濾波,通過增加值域濾波器,也就是考慮畫素之間的差值,差值越小的臨近畫素權重越大。因此可以對邊緣等高頻區進行一定的保留。
2 ABF相比傳統的BF做了什麼修改?
ABF相比BF,有兩點不一樣:第一點,其值域核的delta自適應,該delta不是一個固定的值,而是基於區域性某種特徵(區域性高斯拉普拉斯運算元)計算得到(下面會細細道來);第二點,值域濾波器的本質是考慮畫素間的差值,差值越小,權重越大,因此可以將值域濾波器看作處理影象的灰度直方圖的一維濾波器。通過修改中心畫素點與領域內畫素的差值大小從而修改原有的權重分佈,從而達到畫素值的變化。因此第二點就是修改中心畫素點與鄰域內畫素的差值,也就是對差值增加一個偏移量
3 為什麼ABF可以增加影象的銳化度?
第一點,值域核的delta自適應,它控制著值域濾波器的寬度,我們知道delta越大(方差越大),各個鄰域畫素的權重差不多,會使得值域濾波器的左右降低,極端情況會等效於空域濾波器。反之delta小,則使得值域濾波器佔主導,該雙邊濾波器的權重更多的靠值域濾波器。可以發現delta只是一種銳化增強的前提,僅僅是保證原有的影象銳度,如果要增強影象的銳化度,還得依靠偏移量epslison。文章通過幾張影象形象的表述了為什麼可以增強,我這裡簡單的說一下,值域濾波器通過中心點與鄰域畫素的差值來決定當前鄰域各個畫素的權重。通過權重的修改我們可以使得當前畫素的值得到變化,那麼如何變化就得看當前畫素屬於哪類畫素,本文通過當前畫素的強度與該區域性均值的差值來將當前畫素分為
3. ABF如何確定應該用多大的delta和epslison?
要控制好銳化的效果要同時取決與delta和epslison,那麼如何確定呢?這次採用基於樣本訓練的方法,類似深度學習,通過大量樣本訓練得到。這裡將delta和epslison的求解問題看作一個最小均方誤差問題,將畫素分為T類,因為delta和epslison是一起訓練得到,這個問題沒有閉解,因此設定的一個解空間,delta的範圍為【5,45】,epslison 的範圍為【-60,60】,delta的變化率為1,epslison為2,因此總共的引數組合為50*60 =3000個。 即要確定當畫素值為A類時,應該用那個引數對。因此下一步確定如何對畫素分類,前面我們說可以通過當前畫素與均值的差值確定當前畫素的類別(這裡粗分為3類),根據epslison的值不同需要進一步分類。也就是找到一個合理的特徵,有了好的特徵才能更好的分類,當前畫素值與均值的差值確實很好的關聯了銳化和平滑效果,但是它容易受到噪聲干擾。而考慮特徵點的合理有三點:1.能夠反映邊緣的強度大小;2可以區域當前畫素點屬於哪個區域(邊緣的高低畫素區域或者平滑區);3抗噪聲干擾。
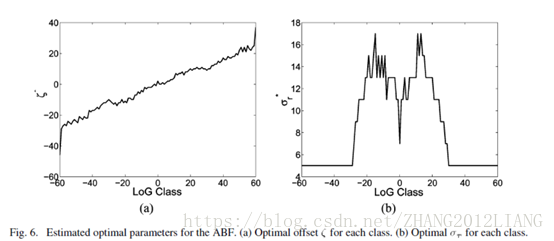
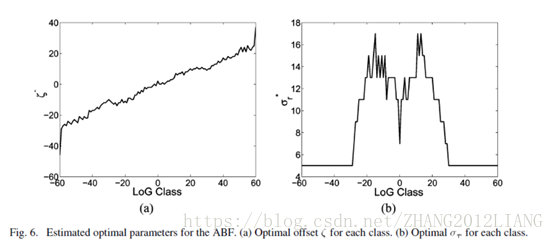
基於特徵的選擇考慮,本文采用的時LOG(高斯拉普拉斯運算元),原因三點:1 它的值反應了當前畫素區域類別(平滑區或者邊緣區域),有一個特例就是當中心點位於邊緣中心,此時LOG的值也為0,跟平滑區一樣,但是還好雙邊濾波還有一個空間域濾波器,作者用圖5解釋了這個特例不影響效果。2,LOG有一個高斯濾波的過程,會對噪聲進行減弱;3,LOG的值的正負可以直接反應當前的中心畫素位於均值的左邊還是右邊也就是邊緣的高畫素區域還是低畫素區域,從而決定epslison的取值。因此epslison的取值不再靠當前中心畫素與均值的差值來決定而是由LOG的值。作者進一步解釋了Log的核的大小以及其delta的取值理由。確定了特徵,通過LOG的輸出值類代表畫素的類別,不同類別的畫素值需要找到最合適的引數對(delta,epslison)。因此作者進行樣本訓練,得出結論見下圖:LOG的輸出值只考慮【-60,60】即畫素一共120種類別,圖a表示epslison與類別幾乎成線性關係即其1/2。圖b則表示delta與類別成一個W型的折線關係。得到了這兩幅圖就可以作用到要處理的影象上了。
4. 為什麼LOG可以用作特徵?
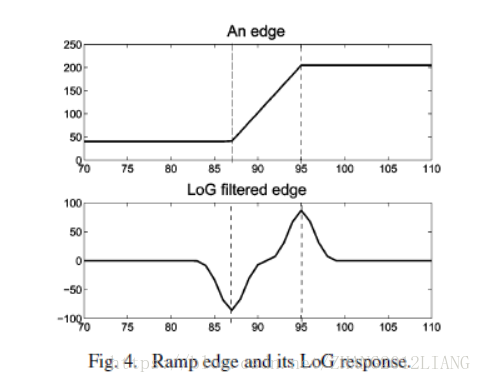
首先看下圖:斜坡邊緣和它對應的LOG反應。邊緣假設為48慢慢的上升到200。我們要做的事就是將這個斜坡變得更陡一點。拉普拉斯運算元屬於一個二階導數,剛好在邊緣中心為0,因此通過0值可以定位到唯一的一條邊,不像一階導數的運算元會檢測出兩條邊。 因此在邊緣低畫素邊,LOG值波谷,高畫素邊,LOG值波峰,邊緣中心為0,很好的區分了畫素類別,再看看訓練出來的delta和epslison與LOG值的關係,epslison偏移量從-30到30,符合前面討論的增強的理論,delta越小,值域所佔權重越大,可以發現從邊緣中心(邊緣橫切面)到低畫素區域的臨界邊或者到高畫素區域的臨界邊都是先增後減。增加時,空間濾波的權重增加,因此可以進行降噪的操作,到達一定時候減少時,又開始增加值域濾波器的權重,確保epslison的效果。為了保證偏移量來產生最大的影響,當LOG小於-29或者大於30時將delta確保較小因此都直接弄到較小值。