貝葉斯和樸素貝葉斯,傻瓜式筆記
阿新 • • 發佈:2018-12-11
目標是調參大師!首先要明白自己在調什麼
貝葉斯定理(抄自資料探勘概念與技術(例子部分有篡改)):設X是資料元組。在貝葉斯的術語中,X看做證據。通常,X用n個屬性集的測量值描述(特徵)。令H為某種假設,如資料元組X屬於某個特定類C。對於分類問題,希望確定給定證據或觀測資料元組X,假設H成立的概率p(H|X)。換言之,給定X的屬性描述,找出元祖X屬於類C的概率。(根據特徵,找到屬於某一類的概率)。
P(H|X)是後驗概率,或在條件X下,H的後驗概率。例如,資料元組由屬性身高,職業,月薪來描述一個人。而X是一個身高190,月薪3000元的學生。令H為某種假設,比如今天中午學生吃肯德基。那麼P(H|X)反映當我們知道身高190,月薪3000,職業是學生時,中午吃肯德基的概率。
相反,P(H)是先驗概率,或H的先驗概率。對於我們的例子,他是任意給定人中午吃肯德基的概率,而不管他的特徵。後驗概率P(H|X)比先驗概率P(H)基於更多的資訊(特徵)。P(H)獨立於X。
類似的,P(X|H)是條件H下,X的後驗概率。也就是,已知一個人中午吃肯德基,那麼他身高190,月薪3000,職業為學生的概率是多少。
P(X)是X的先驗概率。是所有人中身高190,月薪3000,職業為學生的概率是多少。
下面給出貝葉斯公式:
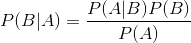
A=X,B=H
樸素貝葉斯:
對於一個月薪300,身高190的學生來說,中午吃肯德基,麥當勞,還是慶豐包子,這三個類別的P(X)是不變的,所以把注意力轉移到P(X|C)P(C)上。(C為具體類別)
對於具有很多屬性的屬性集,計算P(X|C)的開銷可能非常大,為了降低開銷,做出假設,屬性值之間相互獨立,互不相干。(樸素在這了)。然後根據訓練集裡的資料來估算每一項的P(X|C),代入計算即可。
寫給自己看的筆記
