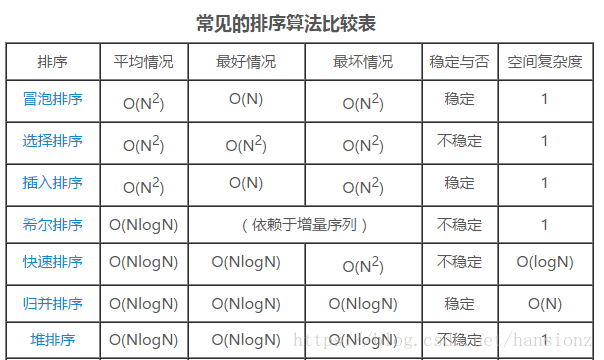
常見排序演算法總結及效能比較
阿新 • • 發佈:2018-12-11
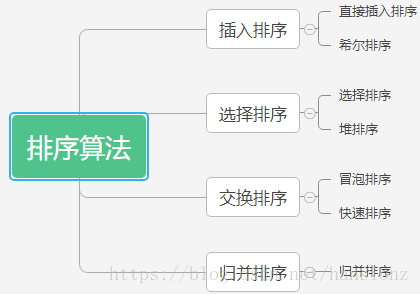
一.常見排序演算法有哪些
二. 插入排序
1.直接插入排序
-
基本思想:插入排序是每次將一個待排序的記錄,按照大小,插入到前面已經排好的有序區中適當的位置,直到將所有記錄插入完位置。大概思想是將待排序記錄放在陣列
R[0..N]中,R[0]是有序區,R[1..N]為無序區,無序區從R[1]開始按照大小插入到有序區中。 -
程式碼實現:
//直接插入排序
int InsertSort(int *num,int len)
{
assert(num);
int i = 0;
//第一個元素已經為有序序列,所以要進行len-1次排序
for (; i < len - 1; 2.希爾排序
-
基本思想:希爾排序是對直接插入排序的優化,它先進行
預排序,使得待排序列基本有序,在進行一次直接插入排序,使得待排序列完全有序。 -
具體實現方法:單獨總結於我的另一篇部落格:希爾排序
三.選擇排序
1.直接選擇排序
- 基本思想:剛開始的時候,有序區沒有元素,每一趟在無序區中選出來一個
最小的元素,然後與無序區第一個元素交換,則此時有序區多一個元素,而無序區少一個元素,直到無序區剩下一個元素結束。 既第一趟排序在R[0…n]中選出一個最小的元素與R[0]交換,第二趟在R[1…n]中選擇最小元素,與第一個與R[1]交換,直到無序區的元素只剩下一個排序完成。 - 程式碼實現:
//選擇排序
void SelectSort(int* num, int len)
{ - 直接排序優化:同時在無序區找出
最大值和最小值下標,先後分別和無序區最左邊最右邊交換(一次確定兩個值) - 具體實現方法見我的另一篇部落格:直接插入排序優化
2.堆排序
-
基本思想:堆排序本質上是一種
樹形選擇排序。它也是對直接選擇排序的一種優化,堆結構在物理儲存上也是一種陣列,但是它在邏輯上是一棵完全二叉樹,在進行堆排序(升序)時,我們可以先建一個大堆,最大的元素在堆頂上,我們可以以O(1)的時間找到最大的元素,然後和最後一個元素交換。此時,這個堆的左右子樹仍然是一個堆,我們只要把[n-1]個數向下調整一次重新建個大堆即可,直到堆中剩下一個元素,既排序完成。 -
排升序–>建大堆 && 排降序–>建小堆
-
具體實現見我的另一篇部落格:堆排序實現
-
程式碼實現:
//向下調堆
void AdjustDown(int* num, int n, int parent)
{
if (num == NULL || n <= 0)
return;
int child = 2 * parent + 1;
while (child < n)
{
//處理讓child指向左右孩子中較大的哪一個
if ((child + 1 < n) && (num[child] < num[child + 1]))
child++;
//比較交換並調整
if (num[child]>num[parent])
{
Swap(&num[child], &num[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
//堆排序
void HeapSort(int* num, int len)
{
if (num == NULL || len <= 0)
return;
//1.建堆(升序->大堆,降序->小堆)
for (int i = (2 * len - 2) / 2; i >= 0; i--)
{
AdjustDown(num, len, i);
}
//2.交換最後一個元素和第一個元素
int end = len - 1;
while (end > 0)
{
Swap(&num[0], &num[end]);
AdjustDown(num, end, 0);
--end;
}
}
四.交換排序
1.氣泡排序
- 基本思想:一次確定一個最大值或者最小值,兩兩比較,將最大值或者最小交換到最右邊或者最左邊,
N個元素需要N-1趟排序。 - 程式碼實現:
//氣泡排序
void BubbleSort(int* num, int len)
{
if (num == NULL || len <= 0)
return;
//確定迴圈躺數
for (int i = 0; i < len - 1; i++)
{
//確定比較次數
for (int j = 0; j < len - 1 - i; j++)
{
if (num[j]>num[j + 1])
Swap(&num[j], &num[j + 1]);
}
}
}
- 氣泡排序還存在幾種優化方法:見我的另一篇部落格氣泡排序的三種優化方法
2.快速排序
- 基本思想:在待排序序列中
任意取一個元素作為基準元素,按照該基準元素將待排序序列分為兩個子序列,左邊子序列的值都小於基準值,右邊子序列的值都大於基準值。然後把左右子序列當做一個子問題,以同樣的方法處理左右子序列,直到所有的元素都排列在相對應的位置上為止。快排是一個遞迴問題,它是按照二叉遞迴樹的前序路線去劃分的。 - 關於快速排序,我詳細將快排的細節總結於我的另一篇部落格:快排總結
五.歸併排序
1.歸併排序
- 基本思想:歸併排序是一個
外排序,它可以對磁碟的檔案進行排序。它將待排序的元素序列分成兩個長度相等的子序列,對每一個子序列排序,然後在將他們合併為一個序列。合併兩個子序列的過程稱為二路歸併。歸併排序主要分為兩步分組和歸併。 - 程式碼實現:
//歸併排序
void MergeSort(int* num, int len)
{
if (num == NULL || len <= 0)
return;
//開闢臨時空間,用來存放每次合併後的子序列
int* tmp = (int*)malloc(sizeof(int)*len);
_MergeSort(num, 0, len - 1, tmp);
//釋放空間
free(tmp);
tmp = NULL;
}
//歸併排序分開過程(遞迴樹按照前序路線展開)
void _MergeSort(int* num, int begin, int end,int* tmp)
{
assert(num&&tmp);
int mid = begin + (end - begin) / 2;
//只有一個元素,說明這個序列已經有序
if (begin == end)
return;
//子問題劃分左子序列
_MergeSort(num, begin, mid, tmp);
//子問題劃分右子序列
_MergeSort(num, mid + 1, end, tmp);
//合併兩個有序陣列
Merge(num, begin, mid, mid + 1, end, tmp);
}
//歸併排序合併過程
void Merge(int* num, int start1, int end1, int start2, int end2, int* tmp)
{
assert(num&&tmp);
int begin = start1;
int index = start1;//從start1的地方合併
//和兩條有序單鏈表的合併的過程類似
while ((start1 <= end1) && (start2 <= end2))
{
if (num[start1] < num[start2])
{
tmp[index++] = num[start1++];
}
else
{
tmp[index++] = num[start2++];
}
}
//把剩餘的合併到tmp上
while (start1 <= end1)
tmp[index++] = num[start1++];
while (start2 <= end2)
tmp[index++] = num[start2++];
//tmp是個臨時空間,最後到把合併的內容拷貝到num上
memcpy(num + begin, tmp + begin, sizeof(int)*(end2 - begin + 1));
}