題目背景

在雙人對決的競技性比賽，如乒乓球、羽毛球、國際象棋中，最常見的賽制是淘汰賽和迴圈賽。前者的特點是比賽場數少，每場都緊張刺激，但偶然性較高。後者的特點是較為公平，偶然性較低，但比賽過程往往十分冗長。

本題中介紹的瑞士輪賽制，因最早使用於18951895年在瑞士舉辦的國際象棋比賽而得名。它可以看作是淘汰賽與迴圈賽的折中，既保證了比賽的穩定性，又能使賽程不至於過長。

題目描述

2 \times N2×N 名編號為 1-2N1−2N 的選手共進行R 輪比賽。每輪比賽開始前，以及所有比賽結束後，都會按照總分從高到低對選手進行一次排名。選手的總分為第一輪開始前的初始分數加上已參加過的所有比賽的得分和。總分相同的，約定編號較小的選手排名靠前。

每輪比賽的對陣安排與該輪比賽開始前的排名有關：第11 名和第22 名、第 33 名和第 44名、……、第2K - 12K−1名和第2K2K名、…… 、第2N - 12N−1名和第2N2N名，各進行一場比賽。每場比賽勝者得11分，負者得 00分。也就是說除了首輪以外，其它輪比賽的安排均不能事先確定，而是要取決於選手在之前比賽中的表現。

現給定每個選手的初始分數及其實力值，試計算在R 輪比賽過後，排名第QQ 的選手編號是多少。我們假設選手的實力值兩兩不同，且每場比賽中實力值較高的總能獲勝。

輸入輸出格式

輸入格式：

第一行是三個正整數N,R ,QN,R,Q,每兩個數之間用一個空格隔開，表示有 2 \times N2×N名選手、RR 輪比賽，以及我們關心的名次 QQ。

第二行是2 \times N2×N 個非負整數s_1, s_2, …, s_{2N}s1​,s2​,…,s2N​，每兩個數之間用一個空格隔開，其中s_isi​表示編號為ii 的選手的初始分數。 第三行是2 \times N2×N 個正整數w_1 , w_2 , …, w_{2N}w1​,w2​,…,w2N​，每兩個數之間用一個空格隔開，其中 w_iwi​ 表示編號為ii 的選手的實力值。

輸出格式：

一個整數，即RR 輪比賽結束後，排名第QQ 的選手的編號。

輸入輸出樣例

輸入樣例#1

2 4 2 
7 6 6 7 
10 5 20 15 

輸出樣例#1

1

說明

【樣例解釋】

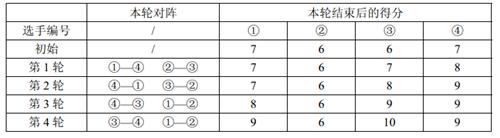
【資料範圍】

對於30\%30%的資料，1 ≤ N ≤ 1001≤N≤100；

對於50\%50%的資料，1 ≤ N ≤ 10,0001≤N≤10,000；

對於100\%100%的資料，1 ≤ N ≤ 100,000,1 ≤ R ≤ 50,1 ≤ Q ≤ 2N,0 ≤ s_1, s_2, …, s_{2N}≤10^8,1 ≤w_1, w_2 , …, w_{2N}≤ 10^81≤N≤100,000,1≤R≤50,1≤Q≤2N,0≤s1​,s2​,…,s2N​≤108,1≤w1​,w2​,…,w2N​≤108。

noip2011普及組第3題。

思路

誰說模擬（%你）是60分？我就AC了！

對於本題，先來bb兩句：

sort肯定超時，因為sort類似於快排，快排就是不斷再序列中間立個flag。
相鄰兩個人分數變化後,有時是不會改變位置的，每次全部修改,所以造成浪費。但是開o2能過（光速逃） 

所以，這才是用歸併排序的精髓。

stable_sort

歸併排序的演算法，和sort基本一致。但是卻只有80分。快讀+o1就過了。（光速逃）

主要是本蒟蒻不會歸併排序。。

#include <stdio.h>
#include <iostream>
#include <algorithm>
#pragma GCC optimize(1)
#define maxsqrt 65536
using namespace std;
int n,r,q;
typedef struct
{
	int id,v,vf;//id編號，v實力值，vf初始值 
}lxydl;//結構體（或聯合體）就有一個特別好的優點：資料統一性 
lxydl a[200001];
int qread()//快讀，哪怕只是快10ms也是好的。 
{
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){ if(ch=='-') f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){ x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
bool cmp(const lxydl &a,const lxydl &b)
{
	if(a.vf!=b.vf) 
		return a.vf>b.vf;//初始實力值高的再前面 
	else 
		return a.id<b.id;//一樣的話就按編號從小往大 
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	register int i,j;
	n=qread(),r=qread(),q=qread();//就是這樣讀入的快讀 
	for(i=1;i<=2*n;i++)
	{
		a[i].vf=qread();//初始實力值 
		a[i].id=i;//編號 
	}
	for(i=1;i<=2*n;i++)
	{
		a[i].v=qread();//實力值 
	}
	stable_sort(a+1,a+n*2+1,cmp);//歸併排序，和sort是一個用法，複雜度O(nlogn)且穩定
	//但是目前最快的排序演算法是倍增排序，複雜度O(n)，可惜再本題是用不了的
	//sort肯定超時，因為sort類似於快排，快排就是不斷再序列中間立個flag
	//相鄰兩個人分數變化後,有時是不會改變位置的，每次全部修改,所以造成浪費。但是開o2能過（光速逃） 
	for(i=1;i<=r;i++)//開始模擬
	{
		for(j=1;j<=2*n;j=j+2)
		{
			if(a[j].v>a[j+1].v)//兩個人的實力比較，如果前一個人比後一個人大 
			{
				a[j].vf++;//前一個人分數+1 
			}
			else//如果前一個人比後一個人小 
			{
				a[j+1].vf++;//後一個人分數+1 
			}
		}
		stable_sort(a+1,a+n*2+1,cmp);//然後將修改好的序列再排序 
	}
	cout<<a[q].id<<endl;//最後的a[q]一定是分最高的 
	return 0;
}