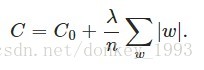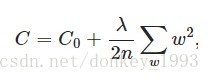吳恩達 改善深層神經網路：超引數除錯、正則化以及優化 課程筆記 

第一週 深度學習裡面的實用層面

1.1 測試集/訓練集/開發集

       原始的機器學習裡面訓練集，測試集和開發集一般按照6:2:2的比例來進行劃分。但是傳統的機器學習的訓練資料很少只需要幾千到幾萬的資料就可以訓練。但是當前基於深度學習的演算法訓練網路的資料有幾百萬張，所以他的開發集和測試集的數量雖然增加了但是由於基數大所以佔得比例變小了可能是9:0.5:0.5這樣。

1.2 偏差和方差

訓練集的錯誤率是：10%

開發集的錯誤率是：12%

偏差 = 訓練集的錯誤率

方差 = 開發集 - 訓練集 = 2%

1.3 正則化問題

正則化可以解決高偏差和過擬合問題。L1和L2正則化是在損失函式的基礎上加上了權重w。λ是正則化引數，通過訓練得到。

L1正則化：

L2正則化：

L2正則化又稱為  權重衰減。

為什麼正則化可以防止過擬合？

直觀的理解：當λ增大，w就會變小，一些神經元就會變為0失效。神經元減少了，網路相對簡單就會緩解過擬合問題。

客觀理解：

如下圖所示，λ增大，w減小，z=w*a+b，對應的z也會減小，z減小了取值範圍就會變小，取值範圍如下圖紅色區域所示。z的取值範圍變小，可以將它的函式看作是一個線性函式（紅色區域），當啟用函式變成線性函式網路就變得線性更加簡單。

1.4 Dropout正則化和其他正則化方法

隨機刪除網路中的神經元。

資料增強，提前終止

1.5 梯度消失和梯度爆炸

假設網路結構如上圖，啟用函式使用簡單f（x）=x。那麼y=w1*w2*w3*...*w9*x。當w>1的時候 y = w^9*x，就會出現梯度爆炸問題，反之當w<1的時候就會出現梯度消失問題。

1.6  梯度檢驗演算法，用來驗證網路訓練是否出現異常。

雙向誤差求得的導數比單向求導更加的準確。