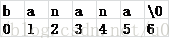1 引言

今天主要看的是樹中的兩個比較重要的資料結構——字首樹和字尾樹。在此之前，先來看兩個問題。（參考部落格：從Trie樹（字典樹）談到字尾樹）

1.1 問題１

一個文字檔案，大約有一萬行，每行一個詞，要求統計出其中最頻繁出現的前10個詞，請給出思想，給出時間複雜度分析。

之前在此文，海量資料處理面試題集錦與Bit-map詳解中給出的參考答案：用Trie樹統計每個詞出現的次數，時間複雜度是O(n*le)（le表示單詞的平均長度），然後是找出出現最頻繁的前10個詞。也可以用堆來實現（具體的操作可參考第三章、尋找最小的k個數），時間複雜度是O(n*lg10)。所以總的時間複雜度，是O(n*le)與O(n*lg10)中較大的哪一個。

1.2 問題2

找出給定字串裡的最長迴文。例子：輸入XMADAMYX。則輸出MADAM。這道題的流行解法是用字尾樹（Suffix Tree)，但其用途遠不止如此，它能高效解決一大票複雜的字串程式設計問題（當然，它有它的弱點，如演算法實現複雜以及空間開銷大），概括如下：

查詢字串S是否包含子串S1。主要思想是：如果S包含S1，那麼S1必定是S的某個字尾的字首；又因為S的字尾樹包含了所有的字尾，所以只需對S的字尾樹使用和Trie相同的查詢方法查詢S1即可（使用字尾樹實現的複雜度同流行的KMP演算法的複雜度相當）。

找出字串S的最長重複子串S1。比如abcdabcefda裡abc同da都重複出現，而最長重複子串是abc。

找出字串S1同S2的最長公共子串。注意最長公共子串（Longest CommonSubstring）和最長公共子序列（Longest CommonSubsequence, LCS）的區別：子串（Substring）是串的一個連續的部分，子序列（Subsequence）則是從不改變序列的順序，而從序列中去掉任意的元素而獲得的新序列；更簡略地說，前者（子串）的字元的位置必須連續，後者（子序列LCS）則不必。比如字串acdfg同akdfc的最長公共子串為df，而他們的最長公共子序列是adf。LCS可以使用動態規劃法解決。

Ziv-Lampel無失真壓縮演算法。 LZW演算法的基本原理是利用編碼資料本身存在字串重複特性來實現資料壓縮，所以一個很好的選擇是使用字尾樹的形式來組織儲存字串及其對應壓縮碼值的字典。

找出字串S的最長迴文子串S1。例如：XMADAMYX的最長迴文子串是MADAM（此即為上面所說的第二個問題：最長迴文問題，本文第二部分將詳細闡述此問題）。

多模式串的模式匹配問題（suffix_array + 二分）。

2 字首樹

2.1 概述

字首樹又名字典樹，單詞查詢樹，Trie樹，是一種多路樹形結構，是雜湊樹的變種，和hash效率有一拼，是一種用於快速檢索的多叉樹結構。

典型應用是用於統計和排序大量的字串（但不僅限於字串），所以經常被搜尋引擎系統用於文字詞頻統計。它的優點是：最大限度地減少無謂的字串比較，查詢效率比雜湊表高。

Trie的核心思想是空間換時間。利用字串的公共字首來降低查詢時間的開銷以達到提高效率的目的。

Trie樹也有它的缺點，Trie樹的記憶體消耗非常大。

性質：不同字串的相同字首只儲存一份。

操作：查詢，插入，刪除。

舉個栗子：給出一組單詞，inn, int, at, age, adv,ant, 我們可以得到下面的Trie：

從上面可以發現一些Trie樹的特性：

1）根節點不包含字元，除根節點外的每一個子節點都包含一個字元。

2）從根節點到某一節點的路徑上的字元連線起來，就是該節點對應的字串。

3）每個節點的所有子節點包含的字元都不相同。

4）每條邊對應一個字母。每個節點對應一項字首。葉節點對應最長字首，即單詞本身。

單詞inn與單詞int有共同的字首“in”, 因此他們共享左邊的一條分支，root->i->in。同理，ate, age, adv, 和ant共享字首"a"，所以他們共享從根節點到節點"a"的邊。

查詢操縱非常簡單。比如要查詢int，順著路徑i -> in -> int就找到了。

搭建Trie的基本演算法也很簡單，無非是逐一把每則單詞的每個字母插入Trie。插入前先看字首是否存在。如果存在，就共享，否則建立對應的節點和邊。比如要插入單詞add，就有下面幾步：

考察字首"a"，發現邊a已經存在。於是順著邊a走到節點a。

考察剩下的字串"dd"的字首"d"，發現從節點a出發，已經有邊d存在。於是順著邊d走到節點ad

考察最後一個字元"d"，這下從節點ad出發沒有邊d了，於是建立節點ad的子節點add，並把邊ad->add標記為d。

2.2 字首樹的應用

字首樹還是很好理解，它的應用也是非常廣的。

（1）字串的快速檢索

字典樹的查詢時間複雜度是O(logL)，L是字串的長度。所以效率還是比較高的。字典樹的效率比hash表高。

hash表：

通過hash函式把所有的單詞分別hash成key值，查詢的時候直接通過hash函式即可，都知道hash表的效率是非常高的為O(1)，當然這是對於如果我們hash函式選取的好，計算量少，且衝突少，那單詞查詢速度肯定是非常快的。那如果hash函式的計算量相對大呢，且衝突律高呢？這些都是要考慮的因素。

還有就是hash表不支援動態查詢，什麼叫動態查詢，當我們要查詢單詞apple時，hash表必須等待使用者把單詞apple輸入完畢才能hash查詢。當你輸入到appl時肯定不可能hash吧。

字典樹（tries樹）：

對於單詞查詢這種，還是用字典樹比較好，但也是有前提的，空間大小允許，字典樹的空間相比較hash還是比較浪費的，畢竟hash可以用bit陣列。

（2）字串排序

從上圖我們很容易看出單詞是排序的，先遍歷字母序在前面。

減少了沒必要的公共子串。

（3）最長公共字首

inn和int的最長公共字首是in，遍歷字典樹到字母n時，此時這些單詞的公共字首是in。

（4）自動匹配字首顯示字尾

我們使用辭典或者是搜尋引擎的時候，輸入appl，後面會自動顯示一堆字首是appl的東東吧。

那麼有可能是通過字典樹實現的，前面也說了字典樹可以找到公共字首，我們只需要把剩餘的字尾遍歷顯示出來即可。

3 字尾樹

3.1 概述

字尾樹，就是把一串字元的所有後綴儲存並且壓縮的字典樹。相對於字典樹來說，字尾樹並不是針對大量字串的，而是針對一個或幾個字串來解決問題。比如字串的迴文子串，兩個字串的最長公共子串等等。

性質：一個字串構造了一棵樹，樹中儲存了該字串所有的字尾。

操作：就是建立和應用。

（1）建立字尾樹

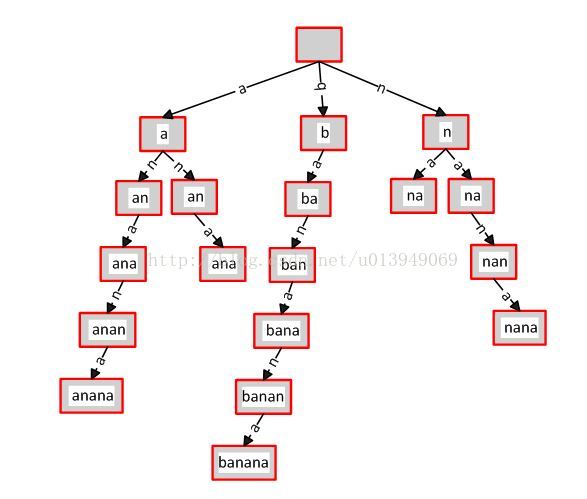
比如單詞banana，它的所有後綴顯示到下面的。0代表從第一個字元為起點，終點不用說都是字串的末尾。

以上面的字尾，我們建立一顆字尾樹。如下圖，為了方便看到字尾，我沒有合併相同的字首。

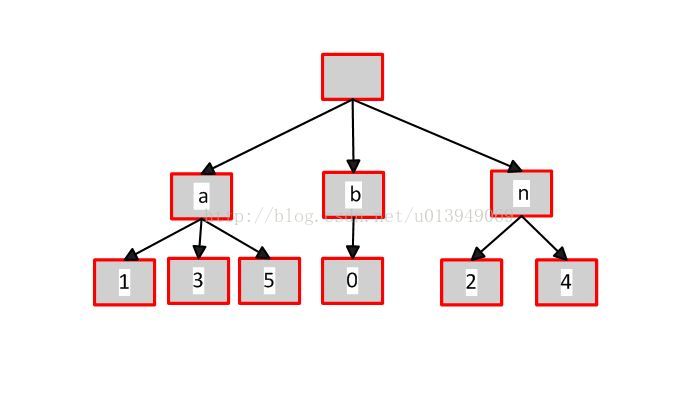
前面簡介的時候我們說了，字尾樹是把一個字串所有後綴壓縮並儲存的字典樹。所以我們把字串的所有後綴還是按照字典樹的規則建立，就成了下圖的樣子。這就是字尾樹的壓縮，可見更加節省空間。

注意還是和字典樹一樣，根節點必須為空。

3.2 字尾樹的應用

字尾樹能解決大多數字符串的問題

（1）查詢某個字串s1是否在另外一個字串s2中

這個很簡單，如果s1在字串s2中，那麼s1必定是s2中某個字尾串的字首。

理解以下字尾串的字首這個詞，其實每個字尾串也就是起始地點不同而已，字首也就是從開頭開始結尾不定。

字尾串的字首就可以組合成該原先字串的任意子串了。

比如banana，anan是anana這個字尾串的字首。

（2）指定字串s1在字串s2中重複的次數

比如說banana是s1，an是s2，那麼計算an出現的次數實際上就是看an是幾個字尾串的字首。

上圖的a節點是儲存所有起始為a字母的字尾串，我們看a字母后的n字母的引用計數即可。

（3）兩個字串S1，S2的最長公共部分（廣義字尾樹）

（4）最長迴文串（廣義字尾樹）

--------------------- 本文來自 lmjy 的CSDN 部落格 ，全文地址請點選：https://blog.csdn.net/u013949069/article/details/78056102?utm_source=copy