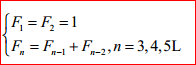（一）奇妙的斐波那契數列：

斐波那契數列的由來是“兔子問題”。

從中總結的規律就是：

（1）每個月小兔子數 = 上個月的大兔子數；

（2）每個月的大兔子數 = 上個月的大兔子數 + 上個月的小兔子數；

（3）每個月的大兔子數 = 上個月的大兔子數 + 上上個月的大兔子數。

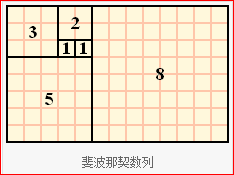
1， 1， 2， 3， 5， 8， 13， 21， 34， 55，89，,144......

即前兩項是1， 1，後面的每一項是前面兩項的和，這就是斐波那契數列。提到數列，作為大學生，學過高等數學，很自然想到求極限。所以，這裡斐波那契數列後一項與前一項比值的極限就是二分之根號五減一，約等於0.618.這就是後面要說的黃金分割比。

遞推公式為：

發現斐波納契數&&尋找斐波那契數列：

1.自然中的斐波那契數：

花基數（花瓣的數目），樹杈的生長， 菜花，松子，

 向日葵：

順時針方向的對數螺線，逆時針方向的對數螺線都是斐波納契數。更為驚人的是，順時針方向的對數螺線和逆時針方向的對數螺線是兩個相繼斐波納契數。還曾經發現過一個更大的向日葵，順時針對數螺線144條，逆時針對數螺線233條。

如下圖：

葉子的生長方式也是如此，對於許多植物來說，每片葉子從中軸附近生長出來，為了在生長的過程中一直都能最佳地利用空間（要考慮到葉子是一片一片逐漸地生長出來，而不是一下子同時出現的），每片葉子和前一片葉子之間的角度應該是222.5度，這個角度稱為“黃金角度”，因為它和整個圓周360度之比是黃金分割數0.618033989……的倒數，而這種生長方式就決定了斐波那契螺旋的產生。向日葵的種子排列形成的斐波那契螺旋有時能達到89，甚至144條。

這就是神祕的大自然！

這些現象是植物生長動力學特性造成的。相鄰器官原基之間的夾角是一個特殊角，這使種子的堆積效率達到最高。

2.斐波那契數列的推廣：

首先，思考一下，斐波那契數列的前兩項是1， 1，那可不可以是1，2呢？

如果是1,2 的話，這就成了缺少第一項的斐波那契數列，即1， 2， 3 ，5， 8，......,這不算是本質的推廣。

次簡單的，如果前兩項是1， 3呢？即1， 3， 4， 7， 11， 18，......

這就是推廣的斐波那契數列，即盧卡斯數列。

盧卡斯數列的相鄰兩項比值的極限恰好也是二分之根號五減一，也是黃金比。所以說，盧卡斯抓住了斐波那契數列的本質。

3.十秒鐘計數：

（1）前n項和 =  第 n + 2 項 - 第 2 項（這是對於盧卡斯數列來說，其實對於斐波那契數列也是適用的）。 

4.楊輝三角中隱藏著斐波那契數列：

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

......

過第一行的1向左下方作45度斜線，之後做直線的平行線，將每條直線所經過的數加起來，即得一數列，1， 1， 2， 3， 5， 8，......

5.還有.一個奇妙的屬性：

從第二項開始，每個奇數項的平方都比前後兩項之積多1；每個偶數項的平方都比前後兩項的平方少1.

6.妙之繼續：

如果任意挑兩個數為起始，比如5， -2.4，然後兩項兩項地加下去，形成5， -2.4， 2.6， 0.2， 2.8， 3， 5.8， 8.8，14.6， 23.4，......，你會發現，

（1）隨著數列的發展，前後兩相之比越來越接近黃金分割比，

（2）且某一項的平方與前後兩項之積的差值也交替相差某個值。

（3）從首項開始，依次計算前一項與後一項的比值，並精確到小數第四位，如果這一工作不斷繼續下去，這個比值將無限趨近於某一個常數，這個常數位於1.6180 與1.6181之間能精確地用黃金數能表示出來。

7.數學中尋找斐波那契數列的足跡： （1）排列組合

有一段樓梯，有10級臺階，規定每一步只能跨一級或跨兩級，要登上第10級臺階，有幾種不同的走法？

這也是一個斐波那契數列：

登第一級臺階，有一種走法；

登第二級臺階，有兩種走法；

登第三級臺階，有三種走法；

登第四級臺階，有五種走法；

......

即1， 2， 3， 5， 8， 13，......而10級，就是89種走法。

（1， 1， 2， 3， 5， 8， 13， 21， 33， 54， 89......）

（2）黃金橢圓

如果一個橢圓和圓的面積相等，那麼這個橢圓就是黃金橢圓。

8.斐波那契數列的應用：

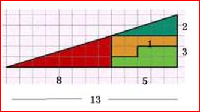
數學遊戲 一位魔術師拿著一塊邊長為8英尺的正方形地毯，對他的地毯匠朋友說：“請您把這塊地毯分成四小塊，再把它們縫成一塊長13英尺，寬5英尺的長方形地毯。”這位匠師對魔術師算術之差深感驚異，因為兩者之間面積相差達一平方英尺呢！

這真是不可思議的事！你猜得到那神奇的一平方英尺究竟跑到哪兒去呢？ 實際上後來縫成的地毯有條細縫，面積剛好就是一平方英尺。 

9.三角形的三邊關係定理與斐波那契數列的一個聯絡：

現有長為144cm的鐵絲，要截成n小段（n > 2），每段的長度不小於1釐米，如果其中任意3段都不能拼成三角形，則n的最大值為多少？

分析：

由於構成三角形的條件是:兩邊之和大於第三邊；反之，如果邊之和不超過（即小於等於）第三邊，則不能構成三角形。

截成的鐵絲最小為1，因此可以放兩個1，第三個是2，為了n儘可能大，要使剩下來的鐵絲儘量長，因此，每一條線段都是前面相鄰兩段之和，依次為  1， 1， 2， 3， 5， 8， 13， 21， 35， 55，以上各數之和為143，與144差1，因此可以取最後一段為56，此時n最大為10.

經過分析，我們發現，“每段的長度的小於1”這個條件起到了控制全域性的作用。正是這個最小數1產生了斐波那契數列，如果把1換成其他數，遞推關係保留了，

但是這個數列消失了。這裡，三角形的三邊關係定理與斐波那契數列發生了聯絡。

在上面的問題中，144 > 143，這個143就是前n項的和，我們把144超出143的部分加到最後一個數上去，如果加到其他數上，就有三條線段可以構成三角形了。 

（二）黃金分割比

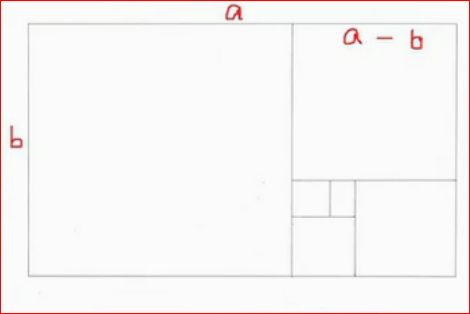
1.黃金矩形：一個矩形，從中減去一個最大的正方形，剩下的矩形的寬與長之比與原來一樣，即剩下的矩形與原來相似。則稱具有這種長寬之比的矩形為黃金矩形。黃金矩形可以按上述方法無限地分割下去。

2.黃金分割：

把任一線段分割成兩段，使 大段/全段 = 小段/大段， 這樣的分割叫做黃金分割。

這樣的比值經過計算之後，就是黃金分割比（可以有兩個分割點,並且關於終點對稱），

x^2 + x - 1 = 0

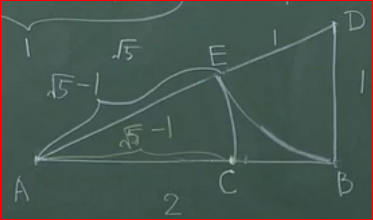
尺規作圖，做出黃金分割點

3.黃金連分數：

這不是一個普通的分數，而是一個分母上有無窮多個“1”的繁分數，通常稱這樣的分數為連分數。

上述連分數可以看做是x = 1 / ( x + 1)中，把x的表示式反覆代入等號右端所得。這一由1構成的連分數是最簡單的一個連分數，它的值為2分之根號5減1。

4.華羅庚的優選法（0.618法）：

（以下為複製內容）

“優選法”，即對某類單因素問題，用最少的試驗次數找到“最佳點”的方法。

    例如，鍊鋼時要摻入某種化學元素加大鋼的強度，摻入多少最合適？假定已經知道每噸鋼加入該化學元素的數量大約應在 1000 克到2000 克之間，現求最佳加量，誤差不得超過 1 克。最“笨”的方法是分別加入 1001 克，1002 克，…，做 1 千次試驗，就能發現最佳方案。 

    一種動腦筋的辦法是二分法，取 1000 克與 2000 克的中點 1500克。再取進一步二分法的中點 1250 克與 1750 克，分別做兩次試驗。如果 1750 克處效果較差，就刪去 1750 克到 2000 克的一段，如果 1250克處效果較差，就刪去 1000 克到 1250 克的一段。再在剩下的一段中取中點做試驗，比較效果決定下一次的取捨，這種“二分法”會不斷接近最好點，而且所用的試驗次數與上法相比，大大減少。 表面上看來，似乎這就是最好的方法。

    但華羅庚證明了，每次取中點的試驗方法並不是最好的方法；每1次取試驗區間的 0.618 處去做試驗的方法，才是最好的，稱之為“優選法”或“0.618 法”。 華羅庚證明了，這可以用較少的試驗次數，較快地逼近最佳方案。

5.黃金分割點的再生性與摺紙法：

根據黃金分割點的再生性，我們可以設計一種直觀的優選法——“摺紙法”。 仍以上邊“在鋼水中新增某種元素”的問題為例。 用一個有刻度的紙條表達 1000 克——2000 克。在這紙條長度的0.618 的地方劃一條線，在這條線所指示的刻度上做一次試驗，也就是按 1618 克做第一次試驗。 然後把紙條對摺，前一條線落在下一層紙的地方，再劃一條線，這條線在 1382 克處，再按 1382 克做第二次試驗。 

按 1236 克做第三次試驗，再和 1382 克的試驗效果比較，如果1236 克的效果較差，我們就把 1236 克以外的短的一段紙條剪去。再對摺剩下的紙條，找出第四次試驗點是 1472 克。 按 1472 克做試驗後，與 1382 克的效果比較，再剪去效果較差點以外的短的一段紙條，再對摺尋找下一次試驗點，一次比一次接近我們的需要，直到達到我們滿意的精確度。 注意，每次剪掉的都是效果較差點以外的短紙條，保留下的是效果較好的部分，而每次留下紙條的長度是上次長度的 0.618 倍。因此，紙條的長度按 0.618 的k次方倍逐次減小，以指數函式的速度迅速趨於 0。所以，“0.618 法”可以較快地找到滿意的點。事實上，當紙條 長度已經很小時，紙條上的任一個點都可以作為“滿意”的點了，因為最優點就在紙條上，你取的點與最優點的誤差一定小於紙條的長。0.618 這個“黃金比”能產生“優選法”，這告訴我們，美的東西與有用的東西之間，常常是有聯絡的。

用導數的方法求極值是用連續的手段處理最優化問題，優選法“0.618 法”則是用離散的手段處理最優化問題。