矩陣的逆、偽逆、左右逆，最小二乘，投影矩陣
主要內容：
- 矩陣的逆、偽逆、左右逆
- 矩陣的左逆與最小二乘
- 左右逆與投影矩陣
一、矩陣的逆、偽逆、左右逆
1、矩陣的逆
定義：
設A是數域上的一個n階方陣，若在相同數域上存在另一個n階矩陣B，使得： AB=BA=I。 則我們稱B是A的逆矩陣，而A則被稱為可逆矩陣。
可逆條件：
A是可逆矩陣的充分必要條件是，即可逆矩陣就是非奇異矩陣。（當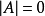
時，A稱為奇異矩陣）
性質：
- 矩陣A可逆的充要條件是A的行列式不等於0。
- 可逆矩陣一定是方陣。
- 如果矩陣A是可逆的，A的逆矩陣是唯一的。
- 可逆矩陣也被稱為非奇異矩陣、滿秩矩陣。
- 兩個可逆矩陣的乘積依然可逆。
- 可逆矩陣的轉置矩陣也可逆。
- 矩陣可逆當且僅當它是滿秩矩陣。
求逆方法：
伴隨矩陣法、初等變換法
2、矩陣的偽逆和左右逆
偽逆矩陣：
偽逆矩陣是逆矩陣的廣義形式。由於奇異矩陣或非方陣的矩陣不存在逆矩陣，但在matlab裡可以用函式pinv(A)求其偽逆矩陣。基本語法為X=pinv(A),X=pinv(A,tol),其中tol為誤差,pinv為pseudo-inverse的縮寫：max(size(A))*norm(A)*eps。函式返回一個與A的轉置矩陣A' 同型的矩陣X，並且滿足：AXA=A,XAX=X.此時，稱矩陣X為矩陣A的偽逆，也稱為廣義逆矩陣。pinv(A)具有inv(A)的部分特性，但不與inv(A)完全等同。 如果A為非奇異方陣，pinv(A)=inv(A)，但卻會耗費大量的計算時間，相比較而言，inv(A)花費更少的時間。
偽逆矩陣求法：
A 為m*n矩陣，r代表矩陣的秩：
若矩陣A是方陣，且|A|!=0，則存在AA-1=E；
若A不是方陣，或者|A|=0，那麼只能求A的偽逆，所謂偽逆是通過SVD計算出來的；
pinv(A)表示A是偽逆：
如果A列滿秩，列向量線性無關，r=n，Ax=b為超定方程組，存在0個或1個解，那麼
，因為
，因此也稱為左逆；
如果A行滿秩，行向量線性無關，Ax=b為欠定方程組，存在0個或無窮個解，那麼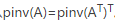
，因為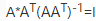
，因此也稱為右逆；
如果秩虧損，那麼只好先做奇異值分解
，U,V是正交陣，D是對角陣；然後取對角陣S，如果D(i,i)=0，那麼S(i,i)=0，如果D(i,i)<>0，那麼S(i,i)=1/D(i,i)。於是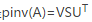
二、矩陣的左逆與最小二乘
其實，最小二乘就是一個超定方程組的求解問題，根據上述的瞭解，超定方程組的求解方法之一就是通過求偽逆的形式，具體來說就是求左逆。即：
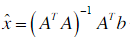
最小二乘也可以從幾何的角度來考慮，那就是下面要說的投影矩陣。
三、左右逆與投影矩陣
左逆中， 
，如果將左逆寫在A右邊將得不到單位矩陣了，那麼 
是什麼？是在A矩陣列空間（A矩陣各列張成的子空間）投影的投影矩陣，它會盡量靠近單位矩陣，一個投影矩陣很想成為單位矩陣，但不可能做到。
右逆中， 
，如果將右逆寫在A左邊也不是單位矩陣了，那
是什麼？是在A矩陣行空間（A矩陣各行張成的子空間）投影的投影矩陣。