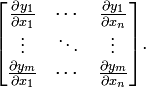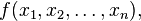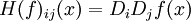雅克比矩陣、海森矩陣與非線性最小二乘間的關係與在SFM和Pose Estimation中的應用
近期,在研究SFM和pose estimation時時常接觸到這三個詞,剛開始不太明白他們間的關係,現將他們整理一下。歡迎吐槽,有什麼不對的地方歡迎指正!
首先,介紹一下三個詞的數學定義與含義:
雅可比矩陣
假設F:Rn→Rm 是一個從歐式n維空間轉換到歐式m維空間的函式。這個函式由m個實函式組成: y1(x1,...,xn), ..., ym(x1,...,xn). 這些函式的偏導數(如果存在)可以組成一個m行n列的矩陣,這就是所謂的雅可比矩陣:
此矩陣表示為:
-
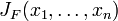 ,或者
,或者 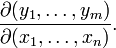
這個矩陣的第i行是由梯度函式的轉置yi(i=1,...,m)表示的
在數學中,海森矩陣
如果 f 所有的二階導數都存在,那麼 f 的海森矩陣即:
其中 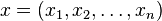 ,即
,即
-

- 解非線性最小二乘法
相關推薦
雅克比矩陣、海森矩陣與非線性最小二乘間的關係與在SFM和Pose Estimation中的應用
近期,在研究SFM和pose estimation時時常接觸到這三個詞,剛開始不太明白他們間的關係,現將他們整理一下。歡迎吐槽,有什麼不對的地方歡迎指正! 首先,介紹一下三個詞的數學定義與含義: 雅可比矩陣 假設F:Rn→Rm 是一個從歐式n維空間轉
關於Matlab中的線性與非線性最小二乘擬合
1、線性最小二乘擬合 最小二乘法(又稱最小平方法)是一種數學優化技術,其通過最小化誤差的平方和尋找資料的最佳函式匹配。利用最小二乘法可以簡便地求得未知的資料,並使得這些求得的資料與實際資料之間誤差的平方和為最小。最小二乘法通過變數的資料來描述變數之間的相互關係。例如通過描述
牛頓法、雅克比矩陣、海森矩陣
一般來說, 牛頓法主要應用在兩個方面, 1, 求方程的根; 2, 最優化。 1,求方程的根 其原理便是使用泰勒展開,然後去線性部分,即: (1) (得到的是x在x0附近的一階線性方程,即下圖中那條切線) 然後令上式等於0,則有:
矩陣的逆、偽逆、左右逆,最小二乘,投影矩陣
主要內容: 矩陣的逆、偽逆、左右逆 矩陣的左逆與最小二乘 左右逆與投影矩陣 一、矩陣的逆、偽逆、左右逆 1、矩陣的逆 定義: 設A是數域上的一個n階方陣,若在相同數域上存在另一個n階矩陣B,使得: AB=BA=I。 則我們稱B是A的逆矩陣,而A則被稱為可逆矩陣。 可逆條件: A是可逆矩陣的充分必要條件是,即可
投影矩陣與最小二乘(二)
咱們繼續說最小二乘的故事,因為Strang把這些東西以一種非常直觀的形式串聯起來,使我迫不及待地想寫一些心得 在上回,我們得到了一個十分重要的東西,投影矩陣: p = A(A'A)-1A' 我們依然以在(一)中的那張投影圖為例,b在平面上的投影是p,如果b垂直於C(A),那
MIT線性代數:16.投影矩陣和最小二乘
線性代數 技術 最小二乘 最小 image 代數 線性 圖片 投影 MIT線性代數:16.投影矩陣和最小二乘
線性代數筆記18——投影矩陣和最小二乘
一維空間的投影矩陣 先來看一維空間內向量的投影: 向量p是b在a上的投影,也稱為b在a上的分量,可以用b乘以a方向的單位向量來計算,現在,我們打算嘗試用更“貼近”線性代數的方式表達。 因為p趴在a上,所以p實際上是a的一個子空間,可以將它看作a放縮x倍,因此向量p可以用p = xa來表示
視覺SLAM常見的QR分解SVD分解等矩陣分解方式求解滿秩和虧秩最小二乘問題
內容一 首先直接給出AX=B解的情況: (1)R(A)< r(A|B),方程組無解 (2)r(A)=r(A|B)=n,方程組有唯一解 (3)r(A)=r(A|B) < n,方程組有無窮解 (4)r(A)>r(A|B),這種
非線性最小二乘法之Gauss Newton、L-M、Dog-Leg原理簡介與實現
double func(const VectorXd& input, const VectorXd& output, const VectorXd& params, double objInd
線性代數 -- 投影矩陣和最小二乘
上一篇文章主要講了子空間的投影, 其中一個主要的知識點是:投影矩陣, P = A(ATA)-1AT, 這個公式的作用就是投影, 比如P*b就是將向量b投影到距離它的列空間最近的位置; 舉兩個極端的例子, 如果向量b位於它自己的列空間中, 那麼向量b在其列空
迴歸學習演算法---偏最小二乘迴歸、PCA降維與理論
1、相關係數的意義與原理 在研究中我們經常要研究多個變數之間的相關性,這些變數可以是自變數與自變數之間、或者是自變數與因變數之間的相關性,為了表示這種相關性,我們引入了相關係數這個概念。這裡使用的
最小二乘擬合(矩陣)
最小二乘公式 B=(XTX)−1XTY 其中, B:n×1矩陣 X:m×n矩陣,輸入變數/特徵 Y:m×1矩陣,輸出變數/目標變數 m:樣本數 n:特徵個數 推導: given:XB=Y →XTXB=XTY →B=(XTX)−1XTY
最大似然估計與最小二乘
現在 最小 bayesian 我不知道 什麽 改變 我不 tps 有關 參考: 最大似然估計,就是利用已知的樣本結果,反推最有可能(最大概率)導致這樣結果的參數值。例如:一個麻袋裏有白球與黑球,但是我不知道它們之間的比例,那我就有放回的抽取10次,結果我發現我抽到了8次黑球
極大既然估計和高斯分布推導最小二乘、LASSO、Ridge回歸
baidu 器) ridge 連續概率 重要 eal 函數 應用 map 最小二乘法可以從Cost/Loss function角度去想,這是統計(機器)學習裏面一個重要概念,一般建立模型就是讓loss function最小,而最小二乘法可以認為是 loss function
【Mark Schmidt課件】機器學習與資料探勘——普通最小二乘
本課件主要內容包括: 有監督學習:迴歸 示例:依賴與解釋變數 數字標籤的處理 一維線性迴歸 最小二乘目標 微分函式最小化 最小二乘解 二維最小二乘 d維最小二乘 偏微分
RANSAC與最小二乘擬合 通俗講解
一、RANSAC理論介紹 普通最小二乘是保守派:在現有資料下,如何實現最優。是從一個整體誤差最小的角度去考慮,儘量誰也不得罪。 RANSAC是改革派:首先假設資料具有某種特性(目的),為了達到目的,適當割捨一些現有的資料。 給出最小二乘擬合(紅線)、RANSAC(綠線)對於一階直線、二階
Spark MLlib協同過濾之交替最小二乘法ALS原理與實踐
請先閱讀leboop釋出的博文《Apache Mahout之協同過濾原理與實踐 》。 基於使用者和物品的協同過濾推薦都是建立在一個使用者-物品評分矩陣(user-item
最大似然估計(MLE)與最小二乘估計(LSE)的區別
最大似然估計與最小二乘估計的區別 標籤(空格分隔): 概率論與數理統計 最小二乘估計 對於最小二乘估計來說,最合理的引數估計量應該使得模型能最好地擬合樣本資料,也就是估計值與觀測值之差的平方和最小。 設Q表示平方誤差,Yi表示估計值,Ŷ
R語言與點估計學習筆記(刀切法與最小二乘估計)
一、 刀切法(jackknife) 刀切法的提出,是基於點估計準則無偏性。刀切法的作用就是不斷地壓縮偏差。但需要指出的是縮小偏差並不是一個好的辦法,因為偏差趨於0時,均方誤差會變得十分大。而且無偏性只有在大量重複時才會表現出與真值的偏差不大。Ja
迭代求解最優化問題——最小二乘問題、高斯牛頓法
最小二乘問題 最小二乘問題是應用最廣泛的優化問題,它的一般形式如下: minx||r(x)||2 該問題的損失函式為S(x)=||r(x)||2。其中r(x)為殘差函式,一般表示預測值與實際值的差別。一個最簡單的最小二乘問題就是線性迴歸問題,對於這個問題的