knn演算法與kd樹實現
- 最近鄰法和k-近鄰法
下面圖片中只有三種豆,有三個豆是未知的種類,如何判定他們的種類?

提供一種思路,即:未知的豆離哪種豆最近就認為未知豆和該豆是同一種類。由此,我們引出最近鄰演算法的定義:為了判定未知樣本的類別,以全部訓練樣本作為代表點,計算未知樣本與所有訓練樣本的距離,並以最近鄰者的類別作為決策未知樣本類別的唯一依據。但是,最近鄰演算法明顯是存在缺陷的,比如下面的例子:有一個未知形狀(圖中綠色的圓點),如何判斷它是什麼形狀?

顯然,最近鄰演算法的缺陷——對噪聲資料過於敏感,為了解決這個問題,我們可以可以把未知樣本週邊的多個最近樣本計算在內,擴大參與決策的樣本量,以避免個別資料直接決定決策結果。由此,我們引進K-最近鄰演算法。K-最近鄰演算法
- KNN演算法實現
演算法基本步驟:
1)計算待分類點與已知類別的點之間的距離
2)按照距離遞增次序排序
3)選取與待分類點距離最小的k個點
4)確定前k個點所在類別的出現次數
5)返回前k個點出現次數最高的類別作為待分類點的預測分類
下面是一個按照演算法基本步驟用python實現的簡單例子,根據已分類的4個樣本點來預測未知點(圖中的灰點)的分類:

from numpy import *
# create a dataset which contains 4 samples with 2 classes
def createDataSet():
# create a matrix: each row as a sample
group = array([[1.0, 0.9], [1.0, 1.0], [0.1, 0.2], [0.0, 0.1]])
labels = ['A', 'A', 'B', 'B'] # four samples and two classes
return group, labels
# classify using kNN (k Nearest Neighbors )
# Input: newInput: 1 x N
# dataSet: M x N (M samples N, features)
# labels: 1 x M
# k: number of neighbors to use for comparison
# Output: the most popular class label
def kNNClassify(newInput, dataSet, labels, k):
numSamples = dataSet.shape[0] # shape[0] stands for the num of row
## step 1: calculate Euclidean distance
# tile(A, reps): Construct an array by repeating A reps times
# the following copy numSamples rows for dataSet
diff = tile(newInput, (numSamples, 1)) - dataSet # Subtract element-wise
squaredDiff = diff ** 2 # squared for the subtract
squaredDist = sum(squaredDiff, axis = 1) # sum is performed by row
distance = squaredDist ** 0.5
## step 2: sort the distance
# argsort() returns the indices that would sort an array in a ascending order
sortedDistIndices = argsort(distance)
classCount = {} # define a dictionary (can be append element)
for i in xrange(k):
## step 3: choose the min k distance
voteLabel = labels[sortedDistIndices[i]]
## step 4: count the times labels occur
# when the key voteLabel is not in dictionary classCount, get()
# will return 0
classCount[voteLabel] = classCount.get(voteLabel, 0) + 1
## step 5: the max voted class will return
maxCount = 0
for key, value in classCount.items():
if value > maxCount:
maxCount = value
maxIndex = key
return maxIndex
if __name__== "__main__":
dataSet, labels = createDataSet()
testX = array([1.2, 1.0])
k = 3
outputLabel = kNNClassify(testX, dataSet, labels, 3)
print "Your input is:", testX, "and classified to class: ", outputLabel
testX = array([0.1, 0.3])
outputLabel = kNNClassify(testX, dataSet, labels, 3)
print "Your input is:", testX, "and classified to class: ", outputLabel 結果如下:
Your input is: [ 1.2 1. ] and classified to class: A
Your input is: [ 0.1 0.3] and classified to class: B
OpenCV中也提供了機器學習的相關演算法,其中KNN演算法的最基本例子如下
 View Code
View Code

>>>
result: [[ 0.]]
neighbours: [[ 0. 0. 0.]]
distance: [[ 65. 145. 178.]]
可以看到KNN演算法將未知點分到第0組(紅色三角形組),從上圖中也可看出3個距離未知點最近的樣本都屬於第0組,因此演算法返回分類標籤也為0。
- KNN演算法的缺陷
觀察下面的例子,我們看到對於樣本X,通過KNN演算法,我們顯然可以得到X應屬於紅點,但對於樣本Y,通過KNN演算法我們似乎得到了Y應屬於藍點的結論,而這個結論直觀來看並沒有說服力。

由上面的例子可見:該演算法在分類時有個重要的不足是,當樣本不平衡時,即:一個類的樣本容量很大,而其他類樣本數量很小時,很有可能導致當輸入一個未知樣本時,該樣本的K個鄰居中大數量類的樣本佔多數。 但是這類樣本並不接近目標樣本,而數量小的這類樣本很靠近目標樣本。這個時候,我們有理由認為該位置樣本屬於數量小的樣本所屬的一類,但是,KNN卻不關心這個問題,它只關心哪類樣本的數量最多,而不去把距離遠近考慮在內,因此,我們可以採用權值的方法來改進。和該樣本距離小的鄰居權值大,和該樣本距離大的鄰居權值則相對較小,由此,將距離遠近的因素也考慮在內,避免因一個樣本過大導致誤判的情況。
從演算法實現的過程可以發現,該演算法存兩個嚴重的問題,第一個是需要儲存全部的訓練樣本,第二個是計算量較大,因為對每一個待分類的樣本都要計算它到全體已知樣本的距離,才能求得它的K個最近鄰點。KNN演算法的改進方法之一是分組快速搜尋近鄰法。其基本思想是:將樣本集按近鄰關係分解成組,給出每組質心的位置,以質心作為代表點,和未知樣本計算距離,選出距離最近的一個或若干個組,再在組的範圍內應用一般的KNN演算法。由於並不是將未知樣本與所有樣本計算距離,故該改進演算法可以減少計算量,但並不能減少儲存量。

- KD樹
實現k近鄰法時,主要考慮的問題是如何對訓練資料進行快速k近鄰搜尋。這在特徵空間的維數大及訓練資料容量大時尤其必要。k近鄰法最簡單的實現是線性掃描(窮舉搜尋),即要計算輸入例項與每一個訓練例項的距離。計算並存儲好以後,再查詢K近鄰。當訓練集很大時,計算非常耗時。為了提高kNN搜尋的效率,可以考慮使用特殊的結構儲存訓練資料,以減小計算距離的次數。
kd樹(K-dimension tree)是一種對k維空間中的例項點進行儲存以便對其進行快速檢索的樹形資料結構。kd樹是是一種二叉樹,表示對k維空間的一個劃分,構造kd樹相當於不斷地用垂直於座標軸的超平面將K維空間切分,構成一系列的K維超矩形區域。kd樹的每個結點對應於一個k維超矩形區域。利用kd樹可以省去對大部分資料點的搜尋,從而減少搜尋的計算量。

對一個三維空間,kd樹按照一定的劃分規則把這個三維空間劃分了多個空間,如下圖所示

類比“二分查詢”:給出一組資料:[9 1 4 7 2 5 0 3 8],要查詢8。如果挨個查詢(線性掃描),那麼將會把資料集都遍歷一遍。而如果排一下序那資料集就變成了:[0 1 2 3 4 5 6 7 8 9],按前一種方式我們進行了很多沒有必要的查詢,現在如果我們以5為分界點,那麼資料集就被劃分為了左右兩個“簇” [0 1 2 3 4]和[6 7 8 9]。因此,根本久沒有必要進入第一個簇,可以直接進入第二個簇進行查詢。把二分查詢中的資料點換成k維資料點,這樣的劃分就變成了用超平面對k維空間的劃分。空間劃分就是對資料點進行分類,“捱得近”的資料點就在一個空間裡面。
構造kd樹的方法如下:構造根結點,使根結點對應於K維空間中包含所有例項點的超矩形區域;通過下面的遞迴的方法,不斷地對k維空間進行切分,生成子結點。在超矩形區域上選擇一個座標軸和在此座標軸上的一個切分點,確定一個超平面,這個超平面通過選定的切分點並垂直於選定的座標軸,將當前超矩形區域切分為左右兩個子區域(子結點);這時,例項被分到兩個子區域,這個過程直到子區域內沒有例項時終止(終止時的結點為葉結點)。在此過程中,將例項儲存在相應的結點上。通常,迴圈的擇座標軸對空間切分,選擇訓練例項點在座標軸上的中位數為切分點,這樣得到的kd樹是平衡的(平衡二叉樹:它是一棵空樹,或其左子樹和右子樹的深度之差的絕對值不超過1,且它的左子樹和右子樹都是平衡二叉樹)。
KD樹中每個節點是一個向量,和二叉樹按照數的大小劃分不同的是,KD樹每層需要選定向量中的某一維,然後根據這一維按左小右大的方式劃分資料。在構建KD樹時,關鍵需要解決2個問題:(1)選擇向量的哪一維進行劃分;(2)如何劃分資料。第一個問題簡單的解決方法可以是選擇隨機選擇某一維或按順序選擇,但是更好的方法應該是在資料比較分散的那一維進行劃分(分散的程度可以根據方差來衡量)。好的劃分方法可以使構建的樹比較平衡,可以每次選擇中位數來進行劃分,這樣問題2也得到了解決。
構造平衡kd樹演算法:
輸入:kk維空間資料集T={x1,x2,...,xN}T={x1,x2,...,xN},其中xi=(x(1)i,x(2)i,...,x(k)i),i=1,2,...,N;xi=(xi(1),xi(2),...,xi(k)),i=1,2,...,N;
輸出:kd樹
(1)開始:構造根結點,根結點對應於包含T的k維空間的超矩形區域。選擇x(1)x(1)為座標軸,以T中所有例項的x(1)x(1)座標的中位數為切分點,將根結點對應的超矩形區域切分為兩個子區域。切分由通過切分點並與座標軸x(1)x(1)垂直的超平面實現。由根結點生成深度為1的左、右子結點:左子結點對應座標x(1)x(1)小於切分點的子區域,右子結點對應於座標x(1)x(1)大於切分點的子區域。將落在切分超平面上的例項點儲存在根結點。
(2)重複。對深度為j的結點,選擇x(l)x(l)為切分的座標軸,l=j%k+1l=j%k+1,以該結點的區域中所有例項的x(l)x(l)座標的中位數為切分點,將該結點對應的超矩形區域切分為兩個子區域。切分由通過切分點並與座標軸x(l)x(l)垂直的超平面實現。由該結點生成深度為j+1的左、右子結點:左子結點對應座標x(l)x(l)小於切分點的子區域,右子結點對應座標x(l)x(l)大於切分點的子區域。將落在切分超平面上的例項點儲存在該結點。
下面用一個簡單的2維平面上的例子來進行說明。
例. 給定一個二維空間資料集:T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},構造一個平衡kd樹。
解:根結點對應包含資料集T的矩形,選擇x(1)x(1)軸,6個數據點的x(1)x(1)座標中位數是6,這裡選最接近的(7,2)點,以平面x(1)=7x(1)=7將空間分為左、右兩個子矩形(子結點);接著左矩形以x(2)=4x(2)=4分為兩個子矩形(左矩形中{(2,3),(5,4),(4,7)}點的x(2)x(2)座標中位數正好為4),右矩形以x(2)=6x(2)=6分為兩個子矩形,如此遞迴,最後得到如下圖所示的特徵空間劃分和kd樹。

下面的程式碼用遞迴的方式構建了kd樹,通過前序遍歷可以進行驗證。這裡只是簡單地採用座標輪換方式選取分割軸,為了更高效的分割空間,也可以計算所有資料點在每個維度上的數值的方差,然後選擇方差最大的維度作為當前節點的劃分維度。方差越大,說明這個維度上的資料越不集中(稀疏、分散),也就說明了它們就越不可能屬於同一個空間,因此需要在這個維度上進行劃分。
# -*- coding: utf-8 -*-
#from operator import itemgetter
import sys
reload(sys)
sys.setdefaultencoding('utf8')
# kd-tree每個結點中主要包含的資料結構如下
class KdNode(object):
def __init__(self, dom_elt, split, left, right):
self.dom_elt = dom_elt # k維向量節點(k維空間中的一個樣本點)
self.split = split # 整數(進行分割維度的序號)
self.left = left # 該結點分割超平面左子空間構成的kd-tree
self.right = right # 該結點分割超平面右子空間構成的kd-tree
class KdTree(object):
def __init__(self, data):
k = len(data[0]) # 資料維度
def CreateNode(split, data_set): # 按第split維劃分資料集exset建立KdNode
if not data_set: # 資料集為空
return None
# key引數的值為一個函式,此函式只有一個引數且返回一個值用來進行比較
# operator模組提供的itemgetter函式用於獲取物件的哪些維的資料,引數為需要獲取的資料在物件中的序號
#data_set.sort(key=itemgetter(split)) # 按要進行分割的那一維資料排序
data_set.sort(key=lambda x: x[split])
split_pos = len(data_set) // 2 # //為Python中的整數除法
median = data_set[split_pos] # 中位數分割點
split_next = (split + 1) % k # cycle coordinates
# 遞迴的建立kd樹
return KdNode(median, split,
CreateNode(split_next, data_set[:split_pos]), # 建立左子樹
CreateNode(split_next, data_set[split_pos + 1:])) # 建立右子樹
self.root = CreateNode(0, data) # 從第0維分量開始構建kd樹,返回根節點
# KDTree的前序遍歷
def preorder(root):
print root.dom_elt
if root.left: # 節點不為空
preorder(root.left)
if root.right:
preorder(root.right)
if __name__ == "__main__":
data = [[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]
kd = KdTree(data)
preorder(kd.root)
進行前序遍歷(前序遍歷首先訪問根結點然後遍歷左子樹,最後遍歷右子樹)的結果如下,可見已經正確構建了kd樹:

搜尋kd樹
利用kd樹可以省去對大部分資料點的搜尋,從而減少搜尋的計算量。下面以搜尋最近鄰點為例加以敘述:給定一個目標點,搜尋其最近鄰,首先找到包含目標點的葉節點;然後從該葉結點出發,依次回退到父結點;不斷查詢與目標點最近鄰的結點,當確定不可能存在更近的結點時終止。這樣搜尋就被限制在空間的區域性區域上,效率大為提高。
用kd樹的最近鄰搜尋:
輸入: 已構造的kd樹;目標點xx;
輸出:xx的最近鄰。
(1) 在kd樹中找出包含目標點xx的葉結點:從根結點出發,遞迴的向下訪問kd樹。若目標點當前維的座標值小於切分點的座標值,則移動到左子結點,否則移動到右子結點。直到子結點為葉結點為止;
(2) 以此葉結點為“當前最近點”;
(3) 遞迴的向上回退,在每個結點進行以下操作:
(a) 如果該結點儲存的例項點比當前最近點距目標點更近,則以該例項點為“當前最近點”;
(b) 當前最近點一定存在於該結點一個子結點對應的區域。檢查該子結點的父結點的另一個子結點對應的區域是否有更近的點。具體的,檢查另一個子結點對應的區域是否與以目標點為球心、以目標點與“當前最近點”間的距離為半徑的超球體相交。如果相交,可能在另一個子結點對應的區域記憶體在距離目標更近的點,移動到另一個子結點。接著,遞迴的進行最近鄰搜尋。如果不相交,向上回退。
(4) 當回退到根結點時,搜尋結束。最後的“當前最近點”即為xx的最近鄰點。
以先前構建好的kd樹為例,查詢目標點(3,4.5)的最近鄰點。同樣先進行二叉查詢,先從(7,2)查詢到(5,4)節點,在進行查詢時是由y = 4為分割超平面的,由於查詢點為y值為4.5,因此進入右子空間查詢到(4,7),形成搜尋路徑:(7,2)→(5,4)→(4,7),取(4,7)為當前最近鄰點。以目標查詢點為圓心,目標查詢點到當前最近點的距離2.69為半徑確定一個紅色的圓。然後回溯到(5,4),計算其與查詢點之間的距離為2.06,則該結點比當前最近點距目標點更近,以(5,4)為當前最近點。用同樣的方法再次確定一個綠色的圓,可見該圓和y = 4超平面相交,所以需要進入(5,4)結點的另一個子空間進行查詢。(2,3)結點與目標點距離為1.8,比當前最近點要更近,所以最近鄰點更新為(2,3),最近距離更新為1.8,同樣可以確定一個藍色的圓。接著根據規則回退到根結點(7,2),藍色圓與x=7的超平面不相交,因此不用進入(7,2)的右子空間進行查詢。至此,搜尋路徑回溯完,返回最近鄰點(2,3),最近距離1.8。
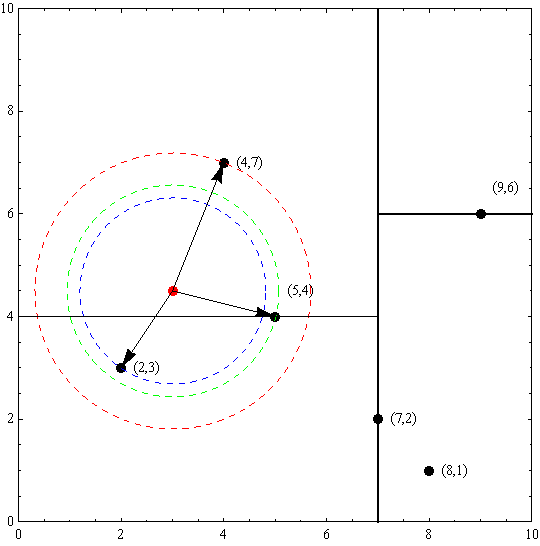
如果例項點是隨機分佈的,kd樹搜尋的平均計算複雜度是O(logN)O(logN),這裡N是訓練例項數。kd樹更適用於訓練例項數遠大於空間維數時的k近鄰搜尋。當空間維數接近訓練例項數時,它的效率會迅速下降,幾乎接近線性掃描。
下面的程式碼對構建好的kd樹進行搜尋,尋找與目標點最近的樣本點:
from math import sqrt
from collections import namedtuple
# 定義一個namedtuple,分別存放最近座標點、最近距離和訪問過的節點數
result = namedtuple("Result_tuple", "nearest_point nearest_dist nodes_visited")
def find_nearest(tree, point):
k = len(point) # 資料維度
def travel(kd_node, target, max_dist):
if kd_node is None:
return result([0] * k, float("inf"), 0) # python中用float("inf")和float("-inf")表示正負無窮
nodes_visited = 1
s = kd_node.split # 進行分割的維度
pivot = kd_node.dom_elt # 進行分割的“軸”
if target[s] <= pivot[s]: # 如果目標點第s維小於分割軸的對應值(目標離左子樹更近)
nearer_node = kd_node.left # 下一個訪問節點為左子樹根節點
further_node = kd_node.right # 同時記錄下右子樹
else: # 目標離右子樹更近
nearer_node = kd_node.right # 下一個訪問節點為右子樹根節點
further_node = kd_node.left
temp1 = travel(nearer_node, target, max_dist) # 進行遍歷找到包含目標點的區域
nearest = temp1.nearest_point # 以此葉結點作為“當前最近點”
dist = temp1.nearest_dist # 更新最近距離
nodes_visited += temp1.nodes_visited
if dist < max_dist:
max_dist = dist # 最近點將在以目標點為球心,max_dist為半徑的超球體內
temp_dist = abs(pivot[s] - target[s]) # 第s維上目標點與分割超平面的距離
if max_dist < temp_dist: # 判斷超球體是否與超平面相交
return result(nearest, dist, nodes_visited) # 不相交則可以直接返回,不用繼續判斷
#----------------------------------------------------------------------
# 計算目標點與分割點的歐氏距離
temp_dist = sqrt(sum((p1 - p2) ** 2 for p1, p2 in zip(pivot, target)))
if temp_dist < dist: # 如果“更近”
nearest = pivot # 更新最近點
dist = temp_dist # 更新最近距離
max_dist = dist # 更新超球體半徑
# 檢查另一個子結點對應的區域是否有更近的點
temp2 = travel(further_node, target, max_dist)
nodes_visited += temp2.nodes_visited
if temp2.nearest_dist < dist: # 如果另一個子結點記憶體在更近距離
nearest = temp2.nearest_point # 更新最近點
dist = temp2.nearest_dist # 更新最近距離
return result(nearest, dist, nodes_visited)
return travel(tree.root, point, float("inf")) # 從根節點開始遞迴
下面結合前面寫的程式碼來進行一下測試:
from time import clock
from random import random
# 產生一個k維隨機向量,每維分量值在0~1之間
def random_point(k):
return [random() for _ in range(k)]
# 產生n個k維隨機向量
def random_points(k, n):
return [random_point(k) for _ in range(n)]
if __name__ == "__main__":
data = [[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]] # samples
kd = KdTree(data)
ret = find_nearest(kd, [3,4.5])
print ret
N = 400000
t0 = clock()
kd2 = KdTree(random_points(3, N)) # 構建包含四十萬個3維空間樣本點的kd樹
ret2 = find_nearest(kd2, [0.1,0.5,0.8]) # 四十萬個樣本點中尋找離目標最近的點
t1 = clock()
print "time: ",t1-t0, "s"
print ret2
結果如下圖所示。先是測試了之前例子中距離(3,4.5)最近的點,可以看出正確返回了最近點(2,3)以及最近距離。然後隨機生成了四十萬個三維空間樣本點,並構建kd樹,然後搜尋離(0.1,0.5,0.8)最近的樣本點,並測試用時。為了進行對比我先是使用numpy算出全部四十萬個距離後尋找最近點,結果耗時0.5s左右!!!怎麼能這麼快(⊙▽⊙),然後不用numpy自己在python中計算全部距離,結果耗時2s左右,還是比自己寫的KD樹要快得多...

可能是這種使用遞迴方式建立和搜尋的kd樹本身效率就不是很高(知乎:為什麼說遞迴效率低?)。而且深層遞迴一定要儘量避免,一是不安全,容易導致棧溢位;二是呼叫代價高(遞迴函式呼叫的代價)。可以考慮轉換為迴圈結構。迴圈結構的kd樹實現參考:KDTree example in scipy

