KNN之KD樹實現
KNN之KD樹
KNN是K-Nearest-Neighbors 的簡稱,由Cover和Hart於1968年提出,是一種基本分類與迴歸方法。這裡主要討論分類問題中的k近鄰法。
一般分類方法:•積極學習法 (決策樹歸納):先根據訓練集構造出分類模型,根據分類模型對測試集分類。 •消極學習法 (基於例項的學習法):推遲建模,當給定訓練元組時,簡單地儲存訓練資料(或稍加處理),一直等到給定一個測試元。模型建立步驟:
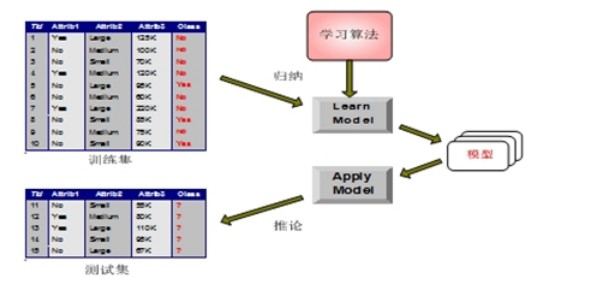
KNN就是一種簡單的消極學習分類方法,它開始並不建立模型,沒有顯式的學習過程。
K近鄰模型由三個基本要素組成:
•距離度量(鄰居判定標準) •K值的選擇(鄰居數量)•分類決策規則(確定所屬類別)
1、距離度量
閔氏距離不是一種距離,而是一組距離的定義(p是一個變引數)。
當p=1時,就是曼哈頓距離
當p=2時,就是歐氏距離
當p→∞時,就是切比雪夫距離
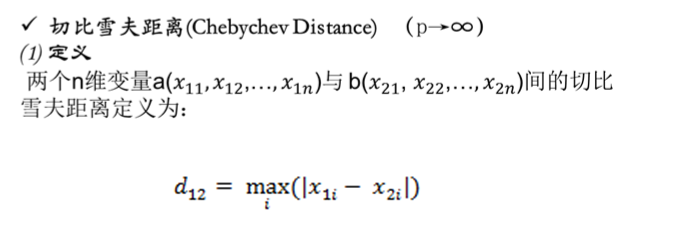
K值的選擇
K值的選擇影響:
1. 如果選擇較小的K值,就相當於用較小的鄰域中的訓練例項進行預測。(極限情況K=1)
優點是“學習”的近似誤差會減小,只有與輸入例項較近或相似的訓練例項才會對預測結果起作用。 缺點是“學習”的估計誤差會增大,對近鄰點的例項點非常敏感。2. 如果選擇較大的K值,就相當於用較大鄰域中的訓練例項進行預測。(極限情況K=N)
優點是可以減少學習的估計誤差,對噪聲不敏感。缺點是學習的近似誤差會增大,與輸入例項較遠(不相似的)訓練例項也會對預測器起作用,使預測發生錯誤。
K值的選擇策略:
Step1:在實際應用中,K先取一個比較小的數值。
Step2:採用交叉驗證法來逐步調整K值,最終選擇適合該樣本的最優的K值。
一般採用k為奇數,跟投票表決一樣,避免因兩種票數相等而難以決策。
分類決策規則(確定所屬類別)常見的分類決策規則:
多數表決:少數服從多數。
由輸入例項的k個鄰近的訓練例項中的多數類決定該例項的類。
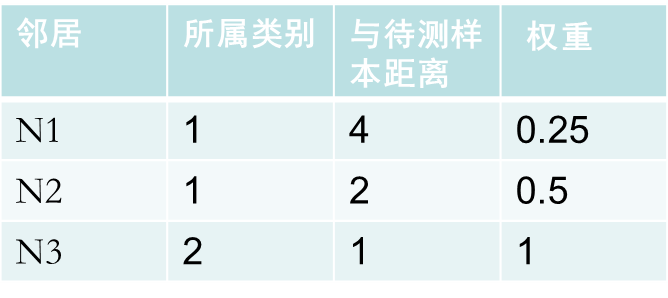
加權表決:類似大眾評審和專家評審。
根據各個鄰居與測試物件距離的遠近來分配相應的投票權重。
最簡單的就是取兩者距離之間的倒數,距離越小,越相似,權重越大,將權重累加,最後選擇累加值最高類別屬性作為該待測樣本點的類別。
例:
類1: 0.25+0.5=0.75
類2:1
所以該待測樣本屬於類2
KNN演算法:
一、最簡單的實現方法線性掃描:對每一個待測樣本點來說,都要對整個樣本集逐一的計算其與待測點的距離,計算並存儲好以後,再查詢K近鄰。
Ø演算法改進:目的:減少計算量,減少儲存量。
(1)採用特殊儲存結構(例:kd樹)
對樣本集進行組織與整理,分群分層,儘可能將計算壓縮到在接近測試樣本鄰域的小範圍內,避免盲目地與訓練樣本集中每個樣本進行距離計算,減少計算量。
(2)裁剪樣本(例:壓縮近鄰演算法,剪輯近鄰法)
在原有樣本集中挑選出對分類計算有效的樣本,使樣本總數合理地減少,以同時達到既減少計算量,又減少儲存量的雙重效果。
二、KD樹的實現方法
Kd-樹 其實是K-dimension tree的縮寫,是對資料點在k維空間中劃分的一種資料結構。其實,Kd-樹是一種平衡二叉樹。
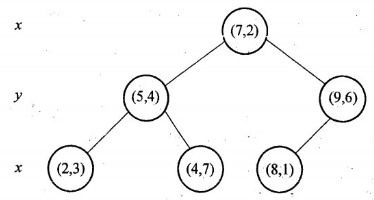
假設有六個二維資料點
= {(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},資料點位於二維空間中。為了能有效的找到最近鄰,Kd-樹採用分而治之的思想,即將整個空間劃分為幾個小部分。六個二維資料點生成的Kd-樹的圖為:
KD樹構建過程:
1.確定:split域=x。具體是:6個數據點在x,y維度上的資料方差分別為39,28.63,所以在x軸上方差更大,故split域值為x;
2.確定:Node-data=(7,2)。具體是:根據x維上的值將資料排序,6個數據的中值(所謂中值,即中間大小的值)為7,所以Node-data域位資料點(7,2)。這樣,該節點的分割超平面就是通過(7,2)並垂直於split=x軸,即直線x=7;
3.確定:左子空間和右子空間。具體是:分割超平面x=7將整個空間分為兩部分:x<=7的部分為左子空間,包含3個節點={(2,3),(5,4),(4,7)};另一部分為右子空間,包含2個節點={(9,6),(8,1)};
4. 遞迴:轉1。對左子空間和右子空間內的資料重複根節點的過程就可以得到一級子節點(5,4)和(9,6),同時將空間和資料集進一步細分,如此往復直到空間中只包含一個數據點。
構建Kd-樹的偽碼為:
演算法:構建Kd-tree
輸入:資料點集Data_Set,和其所在的空間。
輸出:Kd,型別為Kd-tree
1 if data-set is null ,return 空的Kd-tree
2 呼叫節點生成程式
(1)確定split域:對於所有描述子資料(特徵向量),統計他們在每個維度上的資料方差,挑選出方差中最大值,對應的維就是split域的值。資料方差大說明沿該座標軸方向上資料點分散的比較開。這個方向上,進行資料分割可以獲得最好的解析度。
(2)確定Node-Data域,資料點集Data-Set按照第split維的值排序,位於正中間的那個資料點 被選為Node-Data,Data-Set` =Data-Set\Node-data
3 dataleft = {d 屬於Data-Set` & d[:split]<=Node-data[:split]}
Left-Range ={Range && dataleft}
dataright = {d 屬於Data-Set` & d[:split]>Node-data[:split]}
Right-Range ={Range && dataright}
4 :left =由(dataleft,LeftRange)建立的Kd-tree
設定:left的parent域(父節點)為Kd
:right =由(dataright,RightRange)建立的Kd-tree
設定:right的parent域為kd。
KD樹搜尋
現查詢點(2.1,3.1)
1.二叉樹搜尋:先從(7,2)點開始進行二叉查詢,然後到達(5,4),最後到達(2,3),此時搜尋路徑中的節點為<(7,2),(5,4),(2,3)>。首先以(2,3)作為當前最近鄰點,計算其到查詢點(2.1,3.1)的距離為0.1414;
2.回溯查詢:在得到(2,3)為查詢點的當前最近點之後,回溯到其父節點(5,4)。首先判斷該父節點,並不比當前最近點更近,所以無需替換。
接著判斷在該父節點的其他子節點空間中是否有距離查詢點更近的資料點。以(2.1,3.1)為圓心,以0.1414為半徑畫圓,如下圖所示。發現該圓並不和超平面y = 4交割,因此不用進入(5,4)節點右子空間中(圖中灰色區域)去搜索;
3.回溯至根節點:最後,再回溯到(7,2),以(2.1,3.1)為圓心,以0.1414為半徑的圓更不會與x = 7超平面交割,因此不用進入(7,2)右子空間進行查詢。至此,搜尋路徑中的節點已經全部回溯完,結束整個搜尋,返回最近鄰點(2,3),最近距離為0.1414。
KNN分類效能
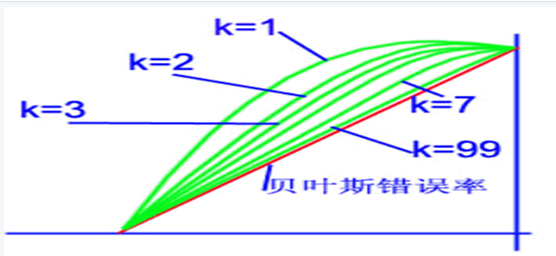
通常情況下,最近鄰法(K=1)的錯誤率高於貝葉斯錯誤率。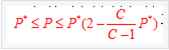
其中P*代表的是貝葉斯誤差率,由於一般情況下P*很小,因此又可粗略表示成:
對於KNN來說,當樣本數量N→∞的條件下,k-近鄰法的錯誤率要低於最近鄰法,具體如圖所示:
參考: