難度：思維題

演算法：逆元+組合數學

題解：

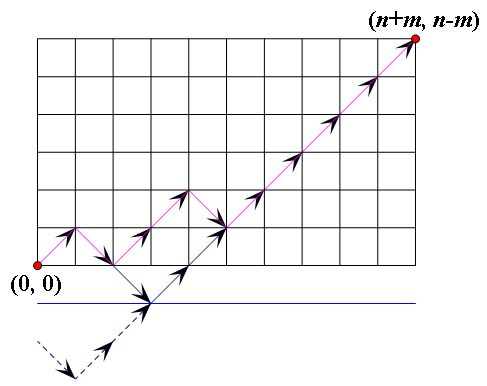
我們設選1為(1,1),選0為(1,-1)

目標是(n+m,n-m)

總方案數為，因為有n+m個位置，放n個1

然後要減去不合法的，即通過y=-1的。將線路與y=-1交點的左邊沿著y=-1做對稱操作，則最後等價於從(0,-2)走到(n+m,n-m)的方案數

所以向上走n-m+2則有

所以不合法方案為C(n+m,n+1)

ans=C(n+m,n)-C(n+m,n+1)

我用的是線性篩逆元，求解。

注意：最後要（......%mod+mod）%mod！！！

程式碼如下：

#include <cstdio>
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>
#define ll long long
#define N 2000005
using namespace std;
const ll p=20100403;
ll inv[N<<1];//一定要開long long 
void invv()
{
	inv[0]=1;
	inv[1]=1;
	for(int i = 2;i <= N;i++)
	{
		inv[i]=(p-p/i)*inv[p%i]%p;
	}
}
ll jc[N];
ll ans1,ans2;
int main()
{
	int n,m;
	scanf("%d%d",&n,&m);
	invv();
	for (int i = 2;i <= n+m;i++)
	{
		inv[i]=(inv[i]*inv[i-1])%p;
	}
	jc[1]=1;
	for(int i = 2;i <= n+m;i++)
	{
		jc[i]=(jc[i-1]*i)%p;
	}
	ans1=((jc[n+m]*inv[n])%p*inv[m])%p;
	ans2=((jc[n+m]*inv[n+1])%p*inv[m-1])%p;
	printf("%lld\n",(ans1-ans2+p)%p);
	return 0 ;
}