洛谷傳送門

題目描述

lxhgww最近接到了一個生成字串的任務，任務需要他把$n$個$1$和$m$個$0$組成字串，但是任務還要求在組成的字串中，在任意的前$k$個字元中，$1$的個數不能少於$0$的個數。現在lxhgww想要知道滿足要求的字串共有多少個，聰明的程式設計師們，你們能幫助他嗎？

輸入輸出格式

輸入格式：

輸入資料是一行，包括$2$個數字$n$和$m$

輸出格式：

輸出資料是一行，包括$1$個數字，表示滿足要求的字串數目，這個數可能會很大，只需輸出這個數除以$20100403$的餘數

輸入輸出樣例

輸入樣例#1：

2 2

輸出樣例#1：

2

說明

limitation

每點$2$秒

對於$30$

對於$100\%$的資料，保證$1\le m\le n\le 1000000$

來源：SCOI 2010

解題分析

可以抽象為$(0,0)$點走到$(n,m)$點， 只能向右或向上， 但不能經過$y=x+1$這條直線， 如下圖：

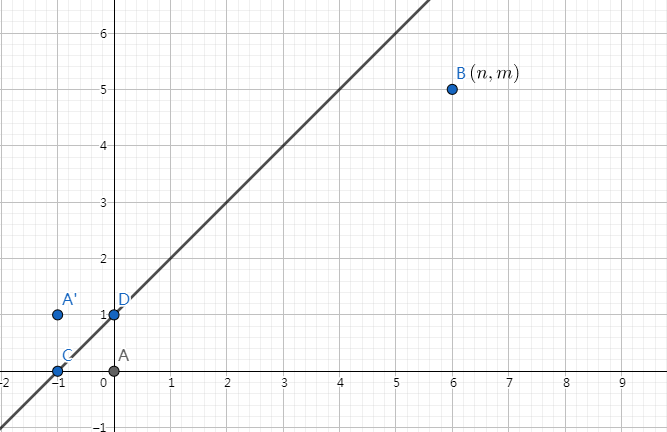
可以做一個對稱點$A'(-1,1)$， 其到$B$點的任何一條合法路徑都會經過$y=x+1$，即不合法方案， 所以合法方案即為$\binom{n+m}{m}-\binom{n+m}{m-1}$

程式碼如下：

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cctype>
#include <algorithm>
#include <cmath>
#define R register
#define IN inline
#define W while
#define gc getchar()
#define MX 2000500
#define ll long long
#define MOD 20100403
 

int fac[MX], inv[MX], sum[MX];
int n, m;
IN int C(R int n, R int m) {return 1ll * fac[n] * sum[m] % MOD * sum[n - m] % MOD;}
int main(void)
{
    inv[0] = inv[1] = fac[1] = sum[1] = 1;
    scanf("%d%d", &n, &m);
    int bd = n + m;
    for (R int i = 2; i <= bd; ++i)
    fac[i] = 1ll * fac[i - 1] * i % MOD, inv[i] = 1ll * (MOD - MOD / i) * inv[MOD % i] % MOD;
    for (R int i = 2; i <= bd; ++i) sum[i] = 1ll * sum[i - 1] * inv[i] % MOD;
    printf("%d", (C(n + m, m) - C(n + m, m - 1) + MOD) % MOD);
}