深度學習 --- CNN
一、卷積神經網路概述
卷積神經網路專門用於處理具有類似網格結構的神經網路,比如說時間序列資料(可認為是在時間軸上有規律地取樣形成的一維網格,舉個例子就是醫學上的心電圖,就是1D影象),然後就是影象資料(二維網格,就是2D影象)
但是,同樣也可以使用一般的神經網路做這方面,可以將每個畫素點當成一個輸入。如果這樣,卷積神經網路的優越性就體現出來了。其優勢主要體現在三個方面:稀疏連線,引數共享,等變表示。這會在之後分析卷積神經網路的結構中的卷積層會具體說明。
二、卷積神經網路結構

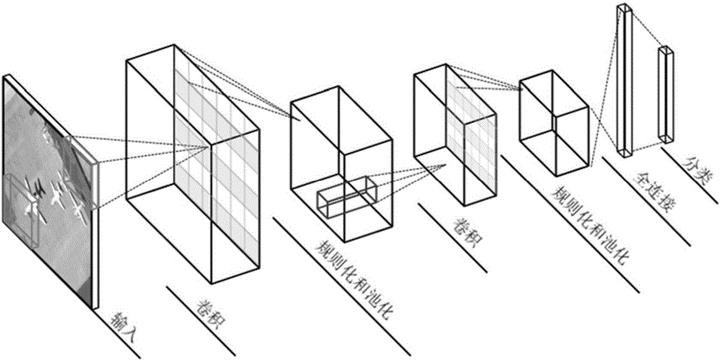
- 輸入層
- 卷積層
- 激勵層
- 池化層
- 全連線層
1.輸入層
輸入層往往做的是影象的預處理,常用的有PCA降維,歸一化等
2.卷積層
卷積過程涉及到三個問題:
- 步長(stride)
- 填補空白(padding)
- 卷積核(kernel/filter)
kernel/filter:與輸入影象資料進行卷積運算的卷積核,在深度學習中,學習的過程也是調整卷積核的引數 的過程
stride:卷積核在原影象資料中水平方向和垂直方向每次步進的長度
padding:卷積運算後,輸出圖片尺寸一般會縮小。同時由於原始圖片邊緣資訊對輸出貢獻較少,輸出可能丟失邊緣資訊,因此通過對原始圖片尺寸擴充套件,擴充套件區補零。
設原始影象尺寸為 ,padding長度
,stride長度
,kernel尺寸
,則輸出影象尺寸:
由於卷積運算的特性,每個單元(畫素點)只會與一部分單元(畫素點)相關聯,而一般神經網路中,每個神經元都是與其他所有的神經元互聯。在卷積神經網路中,這稱作稀疏連線。這樣模型儲存的引數更少了,同時也提高了運算速度。
每個卷積核在進行滑動卷積運算過程中,其引數是共享的,相當於每個卷積核在原始影象中發掘出了一個特徵。將這些特徵按第三維度(2D影象資料)堆疊,例如視訊中有兩個卷積核運算結果的堆疊過程。比如在處理影象時,卷積層的第一層進行影象的邊緣檢測。這一般需要對整個影象進行引數共享,而相對於處理已經剪裁而使其居中的人臉影象是,因為是提取不同位置上的不同特徵,所以一般不對整幅影象做引數共享
由於上述的引數共享,使得卷積神經網路具有平移等變性,即使輸入的某一特徵平移到何處,卷積核都能找到該特徵並呈現出較大的啟用值。例如在處理時間序列的資料時,即使輸入中的某一事件向後延時,在輸出中仍然會有相對於不做延時的表現。
3.激勵層
回顧之前一般的神經網路,對於神經網路某一層(除輸出層),其計算過程:
卷積層的作用類似於之前提到的線性計算,即 ,通過啟用函式
將線性空間對映到非線性空間,在卷積神經網路中,常使用Relu,likely Relu作為啟用函式。
4.池化層
池化層夾雜在連續的卷積層中,用於壓縮資料,防止過擬合現象。
直觀地來說,在處理某個任務的時候,池化層就是為了將圖片資料中最重要的特徵提取出來,去除對該問題不太重要的特徵。
池化層的運算過程如下圖所示:
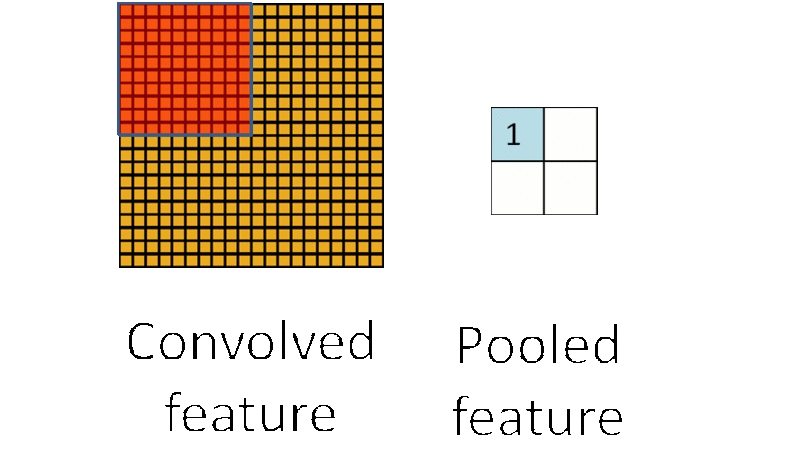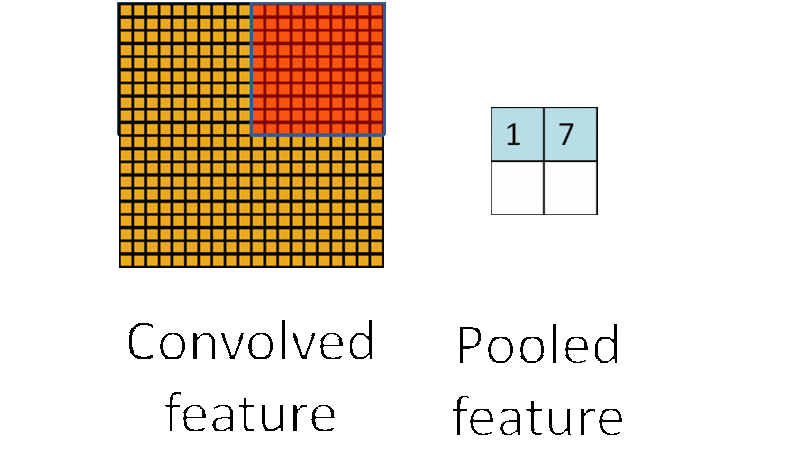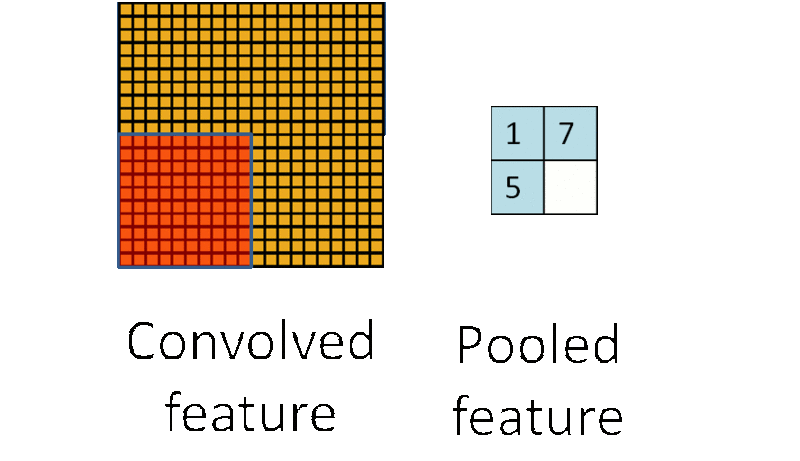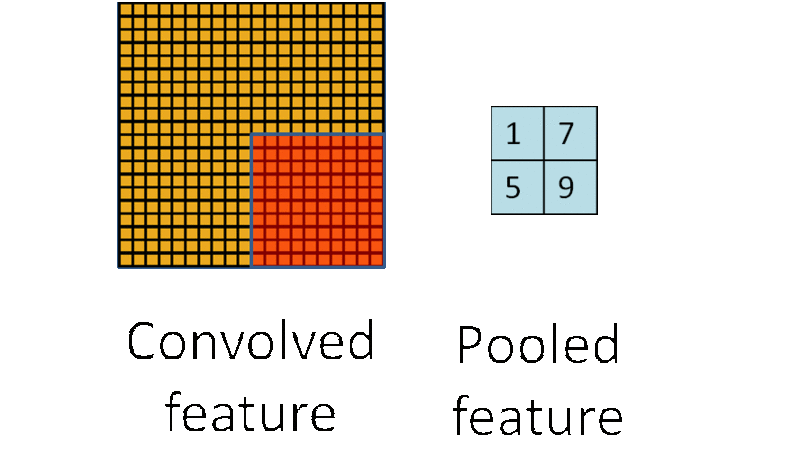

在選擇池化層型別時,一般有max pool 和 average pool,最多使用的是max pool
5.全連線層
全連線層類似於傳統神經網路的連線方式,兩層之間的神經元兩兩相互連線。全連線層在整個模型中往往處於網路的末尾處。

三、卷積神經網路的計算過程
與傳統網路一樣,卷積神經網路也是通過定義代價函式,衡量真實值與預測值之間的差距,逐步調整 等引數以最小化代價函式。
1.卷積層的計算
卷積層的正向傳播計算如下圖所示,輸入影象資料與卷積核對應單元內的引數 相乘並累加,最後再上偏置。

類比於一般的神經網路,經過上述線性計算後,通過激勵層的啟用函式將線性空間對映到非線性空間。
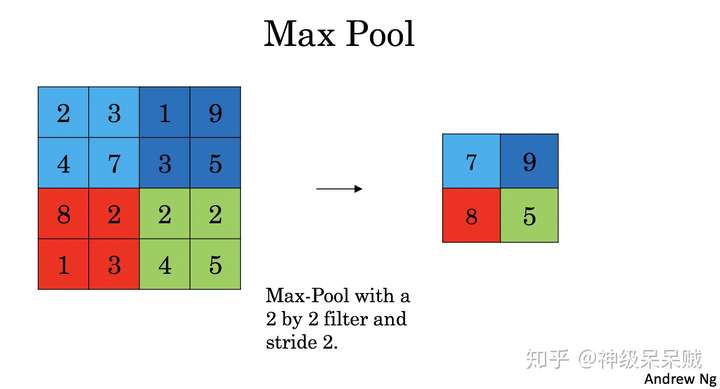
2.池化層的計算
池化層正向傳播主要有 Max Pool 和 Average Pool的計算
對於Max Pool,從滑動視窗每次選定的區域中選擇最大的值,如下圖所示:

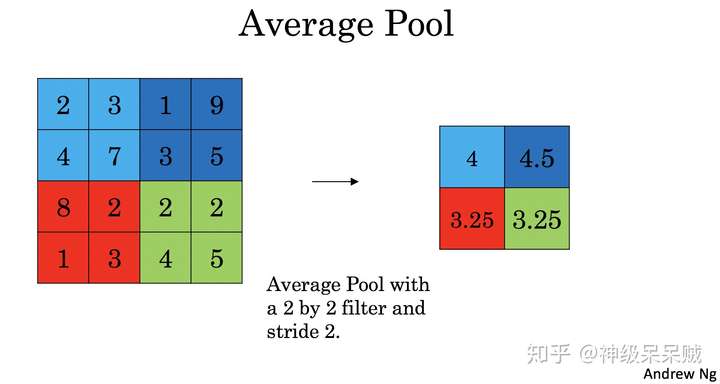
同樣地對於Average Pool,從滑動視窗每次選定的區域中取平均值,如下圖所示: