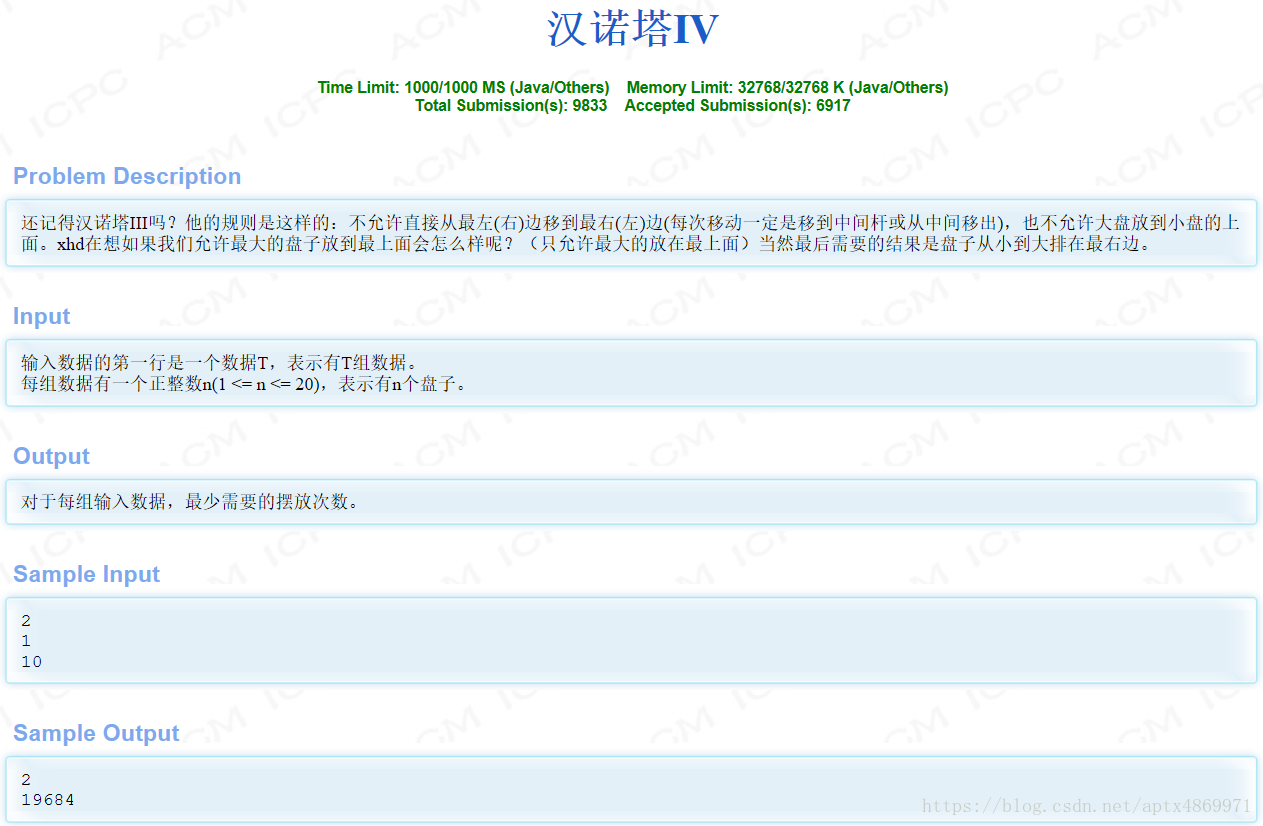
2077 漢諾塔IV 題解
阿新 • • 發佈:2018-12-14
由題意得:
1.此題相較於傳統的漢諾塔問題,多了一個新限制——從左(右)邊到最右(左)邊時,必須經過中間;少了一箇舊限制——允許最大的盤子放到最上面
2.問題就變成了三個步驟:(一)將(n-1)個盤子從最左邊移到中間,(二)然後加“2”,(三)最後再將這(n-1)個盤子從中間移到最右邊
3.由於最大的盤子能夠承載其餘任意盤子,相當於不存在,所以從前後兩面來看,(一)與(三)的步數是一樣的
4.當“n-1”的值為1、2、3時,(一)對應的步數為1、4、7,得推導公式為:3*(n-1)+1
5.當“n”的值為“1”時,只有步驟(二)
6.程式碼如下:
#include<iostream> using namespace std; long long hanoi(int n) { long long f[22]={0}; for(int i=1; i<=n; i++) f[i]=3*f[i-1]+1; return 2*f[n]+2; } int main() { int t,n,i; cin>>t; while(t--) { cin>>n; cout<<hanoi(n-1)<<endl; } return 0; }