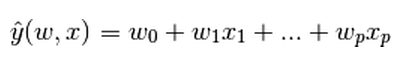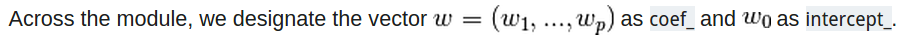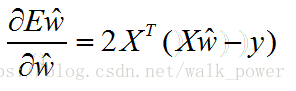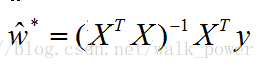【機器學習+sklearn框架】(一) 線性模型之Linear Regression
前言
一、原理
1.演算法含義
2.演算法特點
二、實現
1.sklearn中的線性迴歸
2.用Python自己實現演算法
三、思考(面試常問)
參考
前言
線性迴歸(Linear Regression)基本上可以說是機器學習中最簡單的模型了,但是實際上其地位很重要(計算簡單、效果不錯,在很多其他演算法中也可以看到用其其作為一部分)。機器學習所針對的問題有兩種:一種是迴歸,一種是分類。迴歸是解決連續資料的預測問題,而分類是解決離散資料的預測問題。線性迴歸是一個典型的迴歸問題。其實中學時期我們就接觸過,叫最小二乘法。
一、原理
1.演算法含義
“線性迴歸”試圖學得一個線性模型以儘可能準確地預測實值輸出標記。(《機器學習》--周志華 )
在統計學中,線性迴歸(Linear Regression)是利用稱為線性迴歸方程的最小平方函式對一個或多個自變數和因變數之間關係進行建模的一種迴歸分析。這種函式是一個或多個稱為迴歸係數的模型引數的線性組合(自變數都是一次方)。只有一個自變數的情況稱為簡單迴歸,大於一個自變數情況的叫做多元迴歸。(百度百科)
2.演算法特點
優點:計算簡單,結果易於理解。
缺點:對非線性資料擬合不好。
適用資料型別:數值型和標稱型資料。
二、實現
1.sklearn中的線性迴歸
(1) sklearn對廣義線性模型(Generalized Linear Models)的定義如下:
擬合一條直線使得損失最小,損失可以有很多種,比如平方和最小等等;
【注】y是輸出,x是輸入,輸出是輸入的一個線性組合。
【注】係數矩陣就是coef_,截距就是intercept_
(2) sklearn對廣義線性模型中的線性迴歸演算法(Linear Regression)的定義如下:
首先sklearn將線性迴歸稱做Ordinary Least Squares ( 普通最小二乘法 ),sklearn定義 LinearRegression 類
其實就是解決如下的一個數學問題:
(3)線性迴歸基本圖形
(4)sklear中LinearRegression的引數與實現
成員函式:
fit (X,y) : 以陣列X和y為輸入
成員變數:
coef_ : 儲存線性模型的係數 w儲存
from sklearn import linear_model
reg = linear_model.LinearRegression()
reg.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2])結果如下:
reg.coef_結果如下:
(5) 特殊情況
然而,最小二乘的係數估計依賴於模型特徵項的獨立性。當特徵項相關,並且設計矩陣X 的列近似線性相關時,設計矩陣便接近於一個奇異矩陣,此時最小二乘估計對觀測點中的隨機誤差變得高度敏感,產生較大方差。例如,當沒有試驗設計的收集資料時,可能會出現這種多重共線性(multicollinearity )的情況。
【注】multicollinearity :指線性迴歸模型中的解釋變數之間由於存在精確相關關係或高度相關關係而使模型估計失真或難以估計準確。
本文以sklearn自帶的糖尿病資料集()為例:
Diabetes:包含442個患者的10個生理特徵(年齡,性別、體重、血壓)和一年以後疾病級數指標
載入資料,同時將diabetes糖尿病資料集分為測試資料和訓練資料,其中測試資料為最後20行,訓練資料為前422行。
#資料集獲取
diabetes = datasets.load_diabetes() #載入資料
diabetes_x = diabetes.data[:, np.newaxis] #獲取一個特徵
#資料集劃分
diabetes_x_temp = diabetes_x[:, :, 2]
diabetes_x_train = diabetes_x_temp[:-20] #訓練樣本
diabetes_x_test = diabetes_x_temp[-20:] #測試樣本 後20行
diabetes_y_train = diabetes.target[:-20] #訓練標記
diabetes_y_test = diabetes.target[-20:] #預測對比標記
print(u'劃分行數:', "[總資料量]",len(diabetes_x_temp)," [訓練集]", len(diabetes_x_train)," [測試集]", len(diabetes_x_test))
print(diabetes_x_test) #20行測試資料,每行僅一個特徵
#迴歸訓練及預測
clf = linear_model.LinearRegression()
clf.fit(diabetes_x_train, diabetes_y_train) #注: 訓練資料集測試結果如下:
資料集劃分
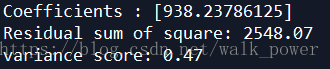
係數,殘差平方和,方差
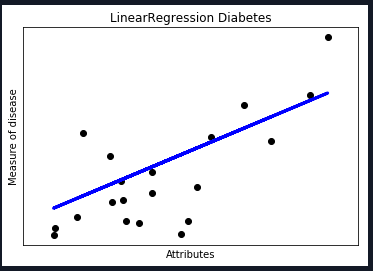
圖形(散點:實際位置 ,直線:預測位置)
2.用Python自己實現演算法
公式推導:
給定資料集D={(x1,y1),(x2,y2),…,(xm,ym)},一共有m個樣本,其中每個樣本有d個屬性,即xi = (xi1,xi2,…,xid)。線性迴歸是試圖學到一個線性模型 f(x) = w1*x1+w2*x2+…+wd*xd + b以儘可能準確的預測實值輸出標記。 其中w=(w1,w2,…,wd), w和b是通過學習之後,模型得以確定。
w和b的確定是通過損失函式確定的:
用最小二乘法對w和b進行估計。把w和b吸收入向量形式,w’ = (w;b),相應的資料集D表示為一個m*(d+1)的矩陣X,其中每一行對應一個示例,該行前d個元素對應於示例的d個屬性值,最後一個元素恆為1。則對於上面的公式有:
對w’求導得:
令上式為零(當X^TX為滿秩矩陣或正定矩陣時可得):
令xi’ = (xi;1)則線性迴歸模型為:
核心公式:,而
import numpy as np
X_=np.linalg.inv(X.T.dot(X)) #呼叫numpy裡的求逆函式
theta=X.dot(X.T).dot(Y) #X.T表示轉置,X.dot(Y)表示矩陣相乘具體實現:
'''
線性迴歸演算法
'''
class LinearRegression_SelfDefined():
def __init__(self): #1.新建變數
self.w = None
def fit(self, X, y): #2.訓練集的擬合
X = np.insert(X, 0, 1, axis=1) #增加一個維度
print (X.shape)
X_ = np.linalg.inv(X.T.dot(X)) #公式:求X的轉置(.T)與X矩陣相乘(.dot(X)),再求其逆矩陣(np.linalg.inv())
self.w = X_.dot(X.T).dot(y) #上述公式與X的轉置進行矩陣相乘,再與y進行矩陣相乘
def predict(self, X): #3.測試集的測試反饋
X = np.insert(X, 0, 1, axis=1) #增加一個維度
y_pred = X.dot(self.w) #X與self.w所表示的矩陣相乘
return y_pred結果如下:
三、思考(面試常問)
1.什麼是線性分類模型,什麼是非線性分類模型,它們各有什麼有優缺點?
區分是否為線性模型,主要是看一個乘法式子中自變數x前的係數w,如果w隻影響一個x(注:應該是說x只被一個w影響),那麼此模型為線性模型。或者判斷決策邊界是否是線性的。不滿足線性模型的情況即為非線性模型。只考慮二類的情形,所謂線性分類器即用一個超平面將正負樣本分離開,表示式為 y=wx 。這裡是強調的是平面。而非線性的分類介面沒有這個限制,可以是曲面,多個超平面的組合等。
線性分類模型(LR,貝葉斯分類,單層感知機、線性迴歸)優缺點:演算法簡單和具有“學習”能力。線性分類器速度快、程式設計方便,但是可能擬合效果不會很好。
非線性分類模型(決策樹、RF、GBDT、多層感知機)優缺點:非線性分類器程式設計複雜,但是效果擬合能力強
2.線性迴歸和邏輯迴歸有什麼區別和聯絡?
①區別:線性迴歸用來預測(如:房價預測),邏輯迴歸用來分類(如:疾病診斷);線性迴歸是擬合函式,邏輯迴歸是預測函式;線性迴歸的引數計算方法是最小二乘法,邏輯迴歸的引數計算方法是梯度下降法。(附上吳恩達講解)
②聯絡:邏輯迴歸比線性迴歸多了一個Sigmoid函式,使樣本能對映到[0,1]之間的數值,用來做分類問題。
3.寫出線性迴歸演算法的步驟並分析其優缺點。
見上文
參考
4. 《機器學習》周志華