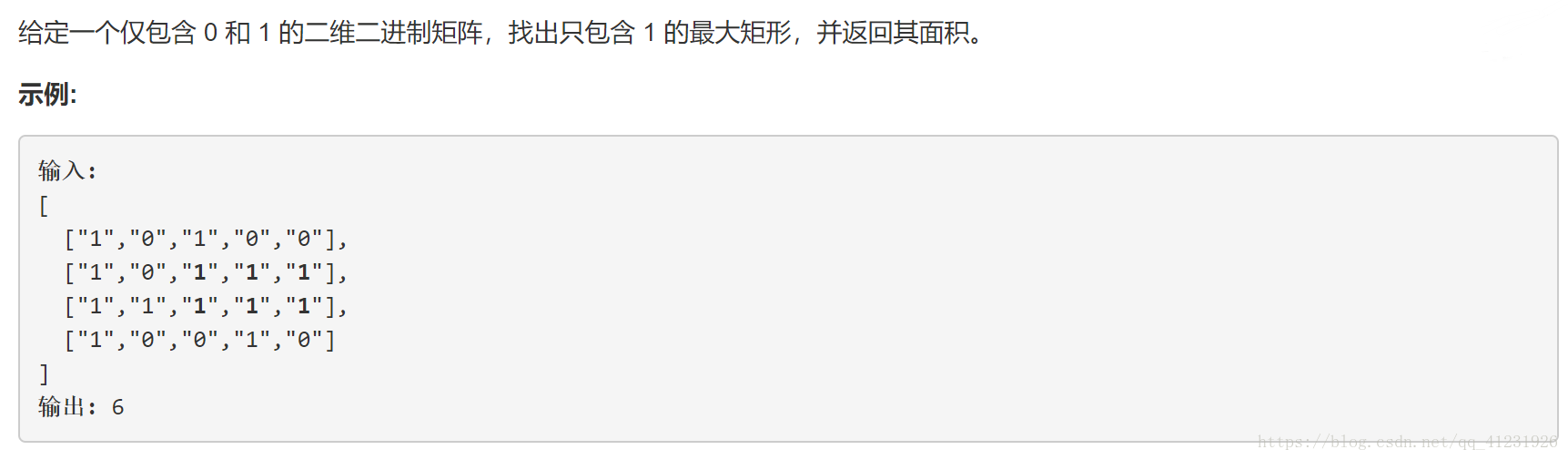
題目描述：

知識點：棧、動態規劃

（1）對於二維陣列matrix中的每一行，計算包括該行及該行之前所有行在內的1的高度。這個過程可以用動態規劃來解決。

狀態定義：

f(x, y)--------第x行第y列位置垂直方向上1的連續高度。

狀態轉移：

當x == 0時，f(x, y) = matrix(x, y) - '0'。這是第一行。

當x > 0時，如果matrix(x, y) == '0'，則f(x, y) = 0。否則，f(x, y) = f(x - 1, y) + 1。

（2）對於每一行，將其看成是有高度的矩形，就是對於每一行求解LeetCode084——柱狀圖中最大的矩形

時間複雜度和空間複雜度均是O(m * n)，其中m為matrix矩陣的行數，n為matrix矩陣的列數。

JAVA程式碼：

public class Solution {

    public int maximalRectangle(char[][] matrix) {
        int m = matrix.length;
        if(m == 0){
            return 0;
        }
        int n = matrix[0].length;
        int[][] heights = new int[m][n];
        for (int i = 0; i < n; i++) {
            heights[0][i] = matrix[0][i] - '0';
        }
        for (int i = 1; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if(matrix[i][j] == '0'){
                    heights[i][j] = 0;
                }else{
                    heights[i][j] = heights[i - 1][j] + 1;
                }
            }
        }
        int result = 0;
        for (int i = 0; i < m; i++) {
            result = Math.max(result, maximalRectangle(heights[i]));
        }
        return result;
    }

    //LeetCode084
    private int maximalRectangle(int[] heights){
        int n = heights.length;
        int[] newHeights = new int[n + 1];
        for (int i = 0; i < n; i++) {
            newHeights[i] = heights[i];
        }
        newHeights[n] = 0;
        int result = 0;
        Stack<Integer> stack = new Stack<>();
        for (int i = 0; i < n + 1; i++) {
            while(!stack.isEmpty() && newHeights[stack.peek()] >= newHeights[i]){
                int index = stack.pop();
                int left = stack.isEmpty() ? -1 : stack.peek();
                result = Math.max(result, (i - left - 1) * newHeights[index]);
            }
            stack.push(i);
        }
        return result;
    }
}
 

LeetCode解題報告：