題解：

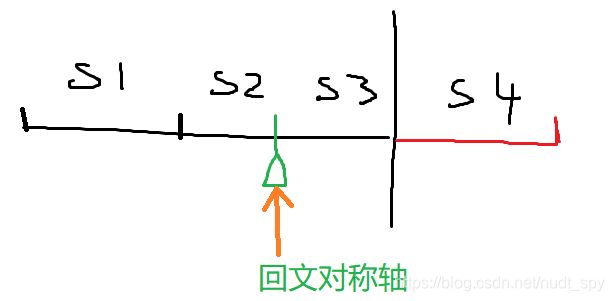
題目的意思就是在第一個串裡找“s1s2s3”，第二個串裡找“s4”，如上拼接後，是一個迴文串，求方案數

可以發現，s1與s4是迴文的，s2和s3是迴文的，我們列舉s1的右端點，s1的長度乘以s2起始點為左邊界的迴文串的數量，累加就是答案。

現在分兩部分，一是求s1，二是求以每個點為左邊界的迴文串的數量

一的話，就是求每個字尾匹配第二個串的LCP，可以用擴充套件kmp求得，也可以用hash加二分求得，二的話，用馬拉車演算法+字首和就可以解決。

程式碼：

#include<bits/stdc++.h>
#define N 1000010
#define INF 0x3f3f3f3f
#define eps 1e-10
#define pi 3.141592653589793
#define mod 998244353
#define LL long long
#define pb push_back
#define cl clear
#define si size
#define lb lower_bound
#define ub upper_bound
#define mem(x) memset(x,0,sizeof x)
#define sc(x) scanf("%d",&x)
#define scc(x,y) scanf("%d%d",&x,&y)
#define sccc(x,y,z) scanf("%d%d%d",&x,&y,&z)
using namespace std;

int lens,lent;
char s[N<<1],t[N],ss[N<<1];
int d[N],r[N<<1];

int Init()
{
    int len = strlen(s+1);
    ss[0] = '$';ss[1] = '#';
    int j = 2;
    for (int i = 1; i <= len; i++)ss[j++] = s[i],ss[j++] = '#';
    ss[j] = '\0';
    return j;
}

void Manacher()
{
    int len=Init();
    int p,mx=0;
    for (int i = 1; i < len; i++)
    {
        if (i<mx) r[i]=min(r[2*p-i],mx-i);else r[i] = 1;
        while (ss[i-r[i]]==ss[i+r[i]]) r[i]++;
        if (mx<i+r[i])p=i,mx=i+r[i];
    }
    for (int i=2;i<len;i++)
    {
        if (ss[i]=='#' && r[i]==1) continue;
        int x=i/2-r[i]/2+1,y=i/2+r[i]/2-!(i&1);
        d[x]++;d[(x+y)/2+1]--;
    }
}

LL p1[N],p2[N],h1[N],h2[N],h3[N],h4[N];

const LL m1=998244353;
const LL m2=100000007;

LL spy(int x,int y)
{
    LL t1=(h1[lens-x+1]-(LL)h1[lens-y]*p1[y-x+1]%m1+m1)%m1;
    LL t2=(h2[lens-x+1]-(LL)h2[lens-y]*p2[y-x+1]%m2+m2)%m2;
    return t1<<31|t2;
}

LL spyer(int y)
{
    return h3[y]<<31|h4[y];
}

int main()
{
    p1[0]=p2[0]=1;
    for (int i=1;i<N;i++) p1[i]=p1[i-1]*377%m1,p2[i]=p2[i-1]*377%m2;

    while(~scanf("%s%s",s+1,t+1))
    {
        mem(d);
        lens=strlen(s+1); lent=strlen(t+1);
        for (int i=1;i<=lens;i++) d[i]=0;
        Manacher();
        for (int i=1;i<=lens;i++) d[i]+=d[i-1];
        strcpy(ss+1,s+1);
        reverse(s+1,s+lens+1);
        for (int i=1;i<=lens;i++)
            h1[i]=(h1[i-1]*377+s[i])%m1,
            h2[i]=(h2[i-1]*377+s[i])%m2;
        for (int i=1;i<=lent;i++)
            h3[i]=(h3[i-1]*377+t[i])%m1,
            h4[i]=(h4[i-1]*377+t[i])%m2;
        LL ans=0;
        for (int i=1;i<lens;i++)
        {
            if (ss[i]!=t[1]) continue;
            int l=1,r=i>lent?lent:i;
            LL k=1;
            while(l<=r)
            {
                int m=l+r>>1;
                if (spy(i-m+1,i)==spyer(m))
                    k=m,l=m+1;else r=m-1;
            }
            ans+=k*d[i+1];
        }
        printf("%lld\n",ans);
    }
}