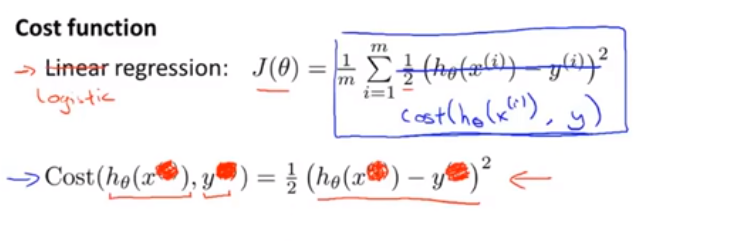Ng | Logistic迴歸
阿新 • • 發佈:2018-12-14
為什麼不用線性迴歸
通常不推薦將線性迴歸用於分類問題
線性迴歸是假設y遠大於1 或者遠小於0的
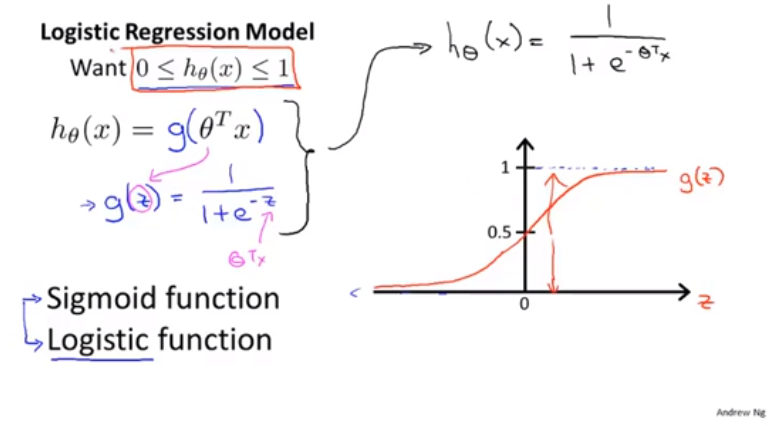
假設陳述
- List item
我們接下來會develope logistic迴歸
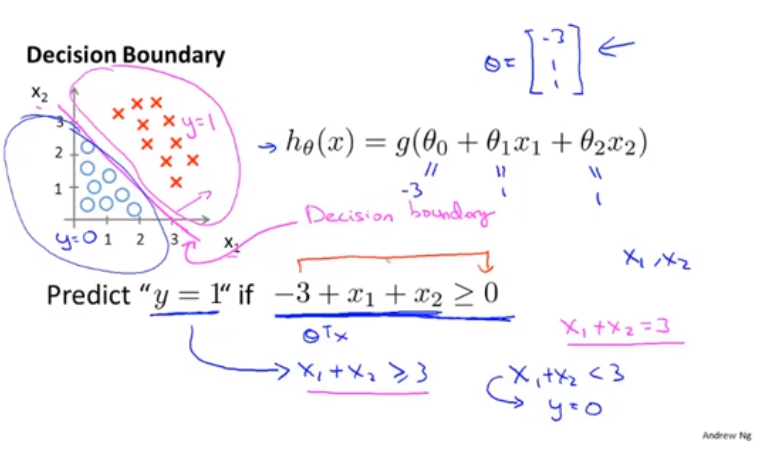
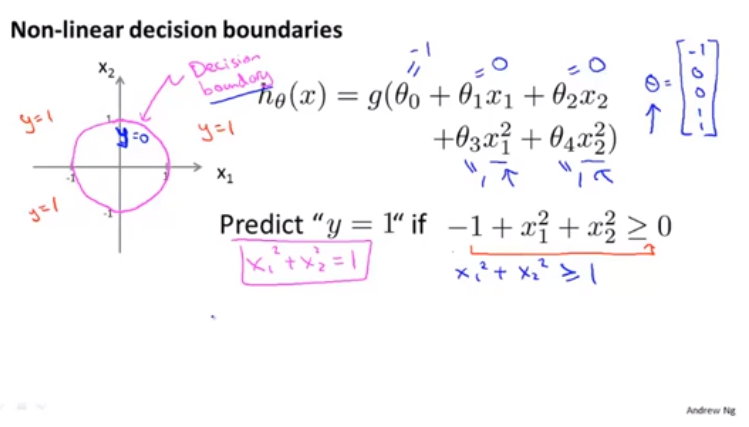
決策界限
讓我們來看看logistic迴歸在計算什麼
決策邊界是假設函式的一個屬性
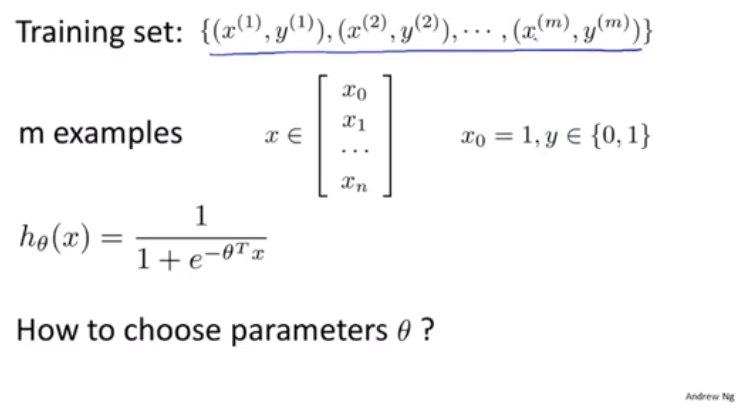
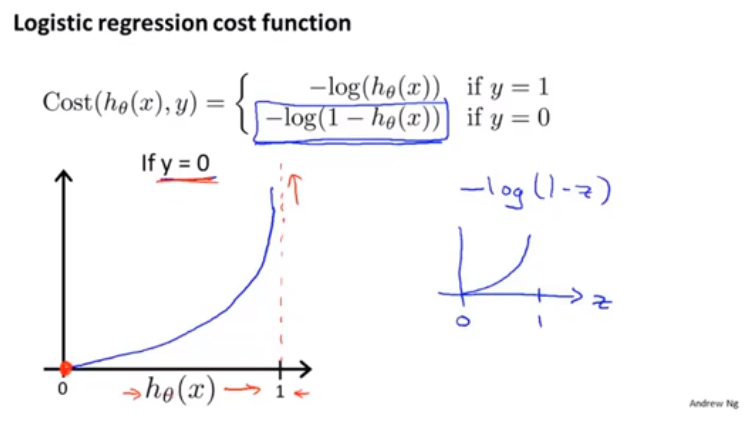
代價函式
如何去擬合函式呢?
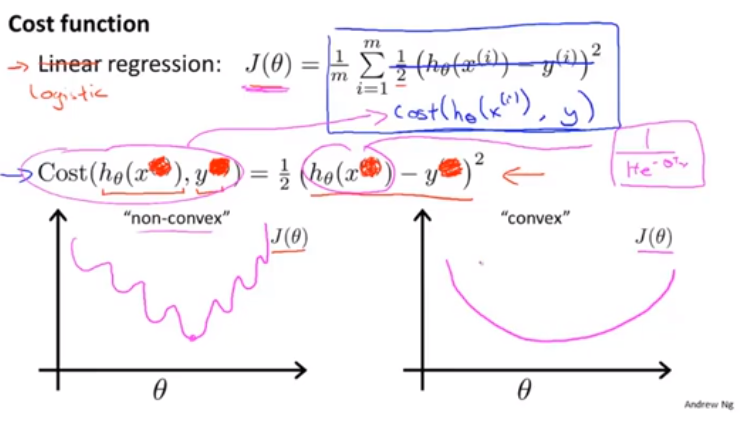
如果是邏輯迴歸,也不是不能用上面這個代價函式,但是如果使用這個,他會變成引數 theta的非凸函式
什麼是非凸函式呢?
左圖是最小二乘法的,非凸 我們想找右圖那樣的
這部分原因,在其他資料看並非如此,而是誤差值很大的時候,斜率很小
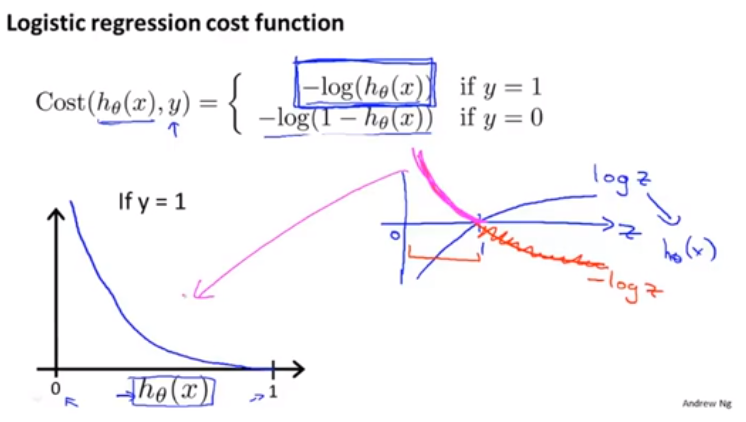
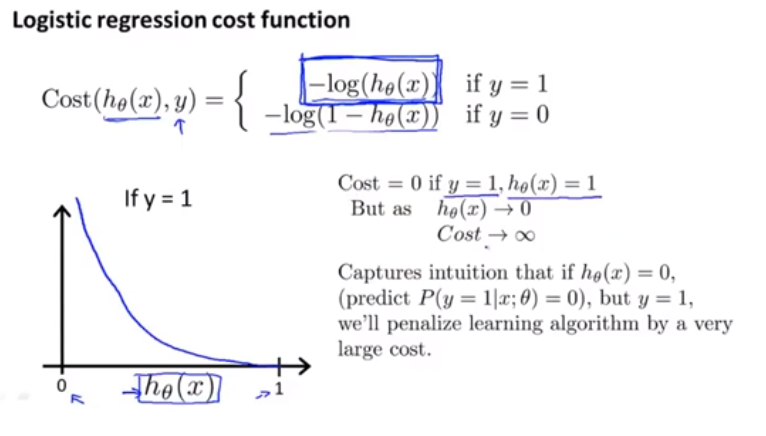
簡化代價函式與梯度
我們會找出一種相對簡單的方法來寫代價函式
聽完這節 你需要實現一個完整的logistic迴歸演算法
這個式子是通過最大似然法得來的
藍色框長這麼像,但是對於h_(theta)發生了變化
線性迴歸是wx 邏輯迴歸是exp(……)^-1
就是假設函式的發生了變化,他倆成了玩去那不同的東西
最後還有一個之前談線性迴歸時,講到的特徵縮放。
高階優化
高階優化演算法和高階優化概念
這些高階優化演算法的思路就是 給出計算導數項和代價函式的方法,有一個智慧內迴圈,事實上它們確實有一個智慧內迴圈,稱為線搜尋演算法。它可以自動嘗試不同的學習速率alpha並自動選擇一個好的學習速率alpha。它們甚至可以為每次迭代選擇不同的學習速率。它們的複雜,並非僅僅為了選擇一個學習率,它們收斂速度也遠遠快於梯度下降。