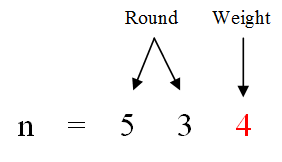《劍指Offer》:從1到n整數中1出現的次數,簡易解法,O(logn)
1、題目來源:
最近在刷題,《劍指offer》當然是不二之選,但是書中偶爾有些解法並不完美。比如第32題,書中給出的解法過於繁複,想在面試極短的時間內完整寫出,難度較大。上網搜尋了一下其他解法,講解的都不太容易理解,故寫了此篇部落格,記錄一下自己的理解。
2、題目描述:
輸入一個整數n,求從1到n這n個整數的十進位制表示中1出現的次數。例如輸入12,從1到12這些整數中包含1的數字有1,10,11和12,1一共出現了5次。
3、具體解法:
暴力的解法一個一個數字考慮,時間複雜度過大,肯定是打動不了面試官,拿下sp的。我們從位的角度來考慮,以三位數534為例。
情況一:個位上出現1
此時將個位固定為1,base記為1。那麼考慮百位的取值為0、1、2、3、4五個數,十位可取0-9十個數,一共有5*10=50種組合。再考慮百位取5,此時因為十位有限制,最大不過3,所以有3+1種組合(501,511,521,531),故總共有count = 53 +1 = 54種(即count = round*base + base)組合。
如果個位(即weight)等於1,n = 531,情況同上,count = 53 + 0 + 1 = round*base + 1 + former;(此時former = 0)
如果個位等於0,n = 530,則531取不到,此時count = 53 = round*base;
情況二:十位上出現1
此時將十位固定為1,base = base * 10 = 10。
如果weight > 1,如weight = 3,n =534,此時考慮百位的取值為0、1、2、3、4、5六個數,個位可取0-9十個數,一共有count = 6*10=round*base + base = 60種組合。
如果weight =1,n = 514,此時當百位為5時,個位就不能取0-9所有數了,如取5,則515就超過514了。此時考慮former的值,個位有0,1,2,3,4五種取法。故count = 5*10 + 4 + 1 = round * base + former + 1;
如果weight = 0,n = 504,此時當百位為5時,十位取不到1,故count = round*base = 5 * 10 = 50;
總結:
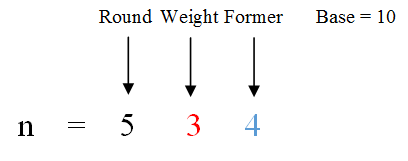
對其它位來說,記每一位的權值為base,位值為weight,該位之前的數是former,則
- 若weight為0,則1出現次數為round*base
- 若weight為1,則1出現次數為 round * base + former + 1
- 若weight大於1,則1出現次數為round*base + base
4、程式碼(java)
class Solution {
public int countDigitOne(int n) {
if (n < 1){
return 0;
}
int count = 0;
int base = 1;
int round = n;
while(round > 0){
int weight = round % 10;
round = round / 10;
count = count + round * base;
if (weight == 1){
count = count + 1 + n%base;
}else if (weight > 1){
count = count + base;
}
base = base * 10;
}
return count;
}
}