TensorFlow之線性迴歸(一)
阿新 • • 發佈:2018-12-16
線性迴歸屬於有監督學習,此類問題,根據帶標註的資訊去訓練一個推斷模型。該模型覆蓋一個數據集,並且對不存在的新樣本進行預測。該模型確定以後,構成模型的運算也就固定。在各運算過程有一些參與運算的數值,在訓練過程不斷更新,使模型能夠學習,並對其輸出進行調整。
雖然推斷不同模型在運算數量和組合方式有很大的不同,但是歸納起來,主要是如下的步驟:
1、初始化模型引數
2、輸入訓練資料
3、在訓練資料上執行推斷模型
4、計算損失函式
5、調整模型引數,返回第二步
現在我們同過線性迴歸,瞭解TensorFlow的訓練過程
線性迴歸
線性迴歸是用來度量變數間關係的統計技術。有意思的是該演算法的實現並不複雜,但可以適用於很多情形。正是因為這些原因,我非常樂意以線性迴歸作為開始學習TensorFlow的開始。
請記住,不管在兩個變數(簡單迴歸)或多個變數(多元迴歸)情形下,線性迴歸都是對一個依賴變數,多個獨立變數xi,一個隨機值b間的關係建模。
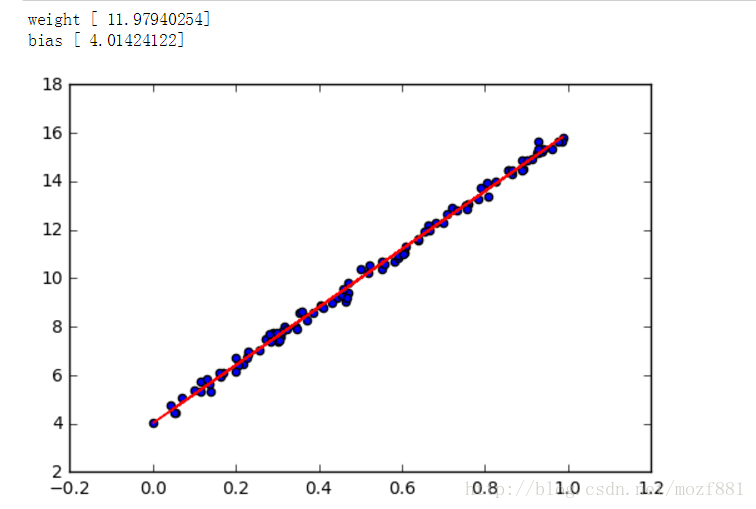
在本小節中,會建立一個簡單的例子來說明TensorFlow如何假設我們的資料模型符合一個簡單的線性迴歸y = W * x + b,為達到這個目的,首先通過簡單的python程式碼在二維空間中生成一系列的點,然後通過TensorFlow尋找最佳擬合這些點的直線。
實現
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
def createdate