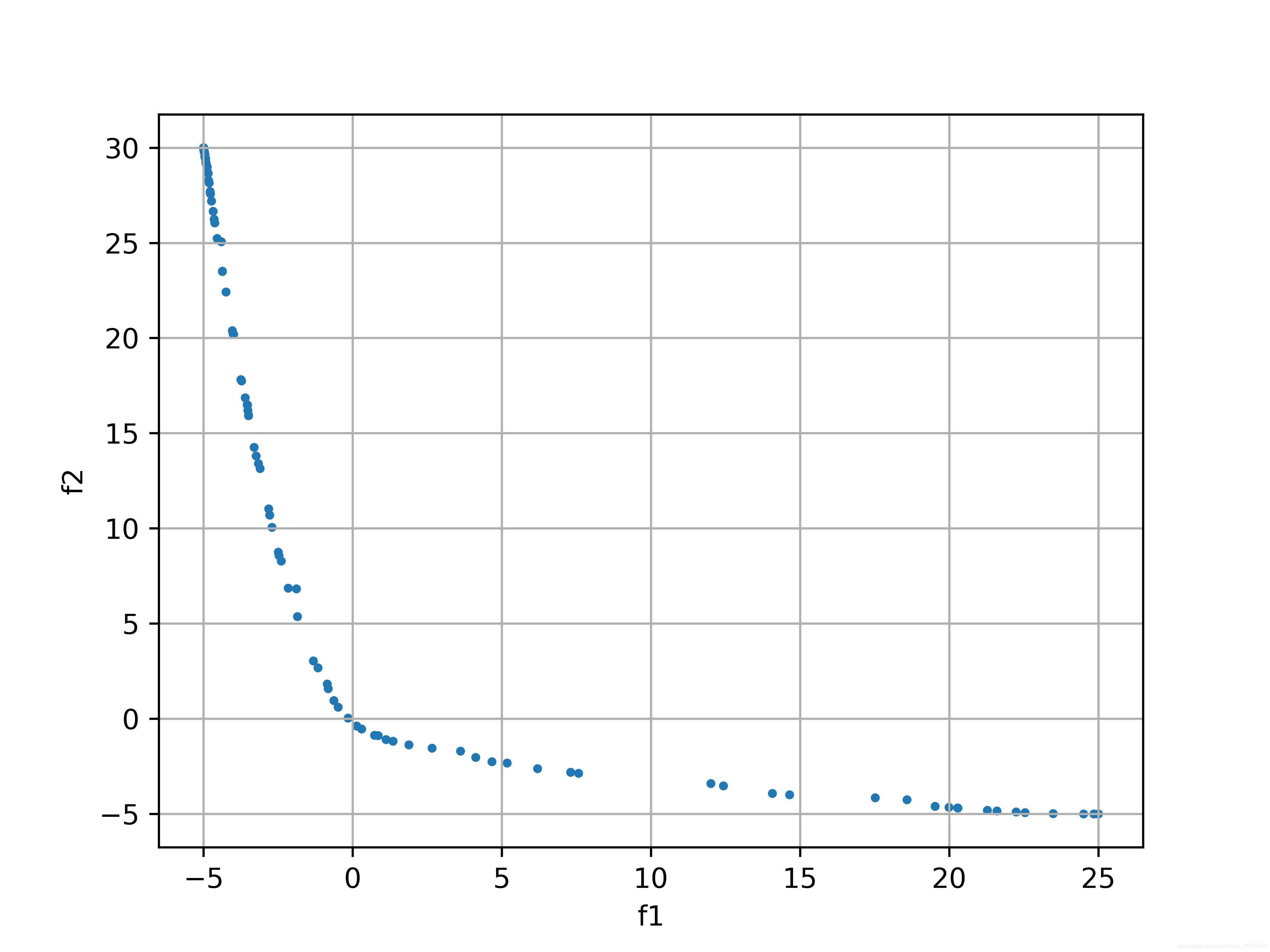
帕累託前沿個數得到的是目標函式值及對應的關係，變數的最優值沒顯示出來。

程式碼（aimfuc.py）

import numpy as np


def aimfuc(x, LegV):  # 定義目標函式
	x1 = x[:, 0]
	x2 = x[:, 1]
	fun1 = (x1 - x2) ** 2 + x1
	fun2 = x1 ** 2 - x2
	return [np.vstack([fun1, fun2]).T, LegV]

程式碼（punishing.py）

# -*- coding: utf-8 -*-

import numpy as np


def punishing(LegV, FitnV):
	FitnV[np.where(LegV == 0)[0]] = np.min(FitnV) * 0.1  # 對非可行解嚴厲懲罰
	return FitnV

 

程式碼（main.py）

# -*- coding: utf-8 -*-

import geatpy as ga
import numpy as np

# 獲取函式介面地址
AIM_M = __import__('aimfuc')
PUN_M = __import__('punishing')
"""============================變數設定============================"""
x1 = [-5, 5]  # 自變數1的範圍
x2 = [-5, 5]  # 自變數2的範圍
b1 = [1, 1]  # 自變數1是否包含下界
b2 = [1, 1]  # 自變數2是否包含上界
precisions = [1, 1]  # 在二進位制/格雷碼編碼中代表自變數的編碼精度，當控制變數是二進位制/格雷編碼時，該引數可控制編碼的精度
ranges = np.vstack([x1, x2]).T  # 生成自變數的範圍矩陣
borders = np.vstack([b1, b2]).T  # 生成自變數的邊界矩陣
# 生成區域描述器
FieldD = ga.crtfld(ranges, borders, precisions)
"""========================遺傳演算法引數設定========================="""
NIND = 50  # 種群規模
MAXGEN = 500  # 最大遺傳代數
MAXSIZE = 200  # 最大帕累託前沿數
GGAP = 0.8  # 代溝：子代與父代的重複率為(1-GGAP)
selectStyle = 'rws'  # 遺傳演算法的選擇方式設為"rws"——輪盤賭選擇
recombinStyle = 'xovdp'  # 遺傳演算法的重組方式，設為兩點交叉
recopt = 0.9  # 交叉概率
pm = 0.1  # 變異概率
SUBPOP = 1  # 設定種群數為1
maxormin = 1  # 設定標記表明這是最小化目標
"""=======================呼叫程式設計模板進行種群進化==================="""
# 呼叫程式設計模板進行種群進化，得到種群進化和變數的追蹤器以及執行時間
[ObjV, NDSet, NDSetObjV, times] = ga.moea_nsga2_templet(AIM_M=AIM_M, AIM_F="aimfuc", PUN_M=PUN_M, PUN_F="punishing",
                                                        FieldDR=FieldD, problem="R", maxormin=1, MAXGEN=MAXGEN,
                                                        MAXSIZE=MAXSIZE, NIND=NIND, SUBPOP=SUBPOP, GGAP=GGAP,
                                                        selectStyle=selectStyle, recombinStyle=recombinStyle,
                                                        recopt=recopt, pm=pm, distribute=True, drawing=1)

 

測試

用時：39.307276010513306 秒
帕累託前沿點個數：200 個
單位時間找到帕累託前沿點個數：5 個