利用匈牙利演算法&Hopcroft-Karp演算法解決二分圖中的最大二分匹配問題 例poj 1469 COURSES
首先介紹一下題意:已知,有N個學生和P門課程,每個學生可以選0門,1門或者多門課程,要求在N個學生中選出P個學生使得這P個學生與P門課程一一對應。
這個問題既可以利用最大流演算法解決也可以用匈牙利演算法解決。如果用最大流演算法中的Edmonds-karp演算法解決,因為時間複雜度為O(n*m*m),n為點數,m為邊數,會超時,利用匈牙利演算法,時間複雜度為O(n*m),時間複雜度小,不會超時。
其實匈牙利演算法就是最大流演算法,只不過它的使用範圍僅限於二分圖,所以可以稱之為“二分圖定製版的最大流演算法”,既然是定製的,那麼他就會考慮到二分圖的特殊性,優化原來的最大流演算法,降低時間複雜度,同時也變得有點複雜不容易理解了。既然匈牙利演算法繼承自最大流演算法,所以他的演算法框架與最大流演算法是一樣的:
最大流演算法與匈牙利演算法的框架:
初始時最大流為0(匈牙利演算法為:最大匹配為空)
while 找到一條增廣路徑(匈牙利演算法為:取出未遍歷的左邊的點u)
最大流+=增廣路徑的流量,更新網路(匈牙利演算法為:如果點u存在增廣路徑,增廣路徑取反,最大匹配增加1對匹配)
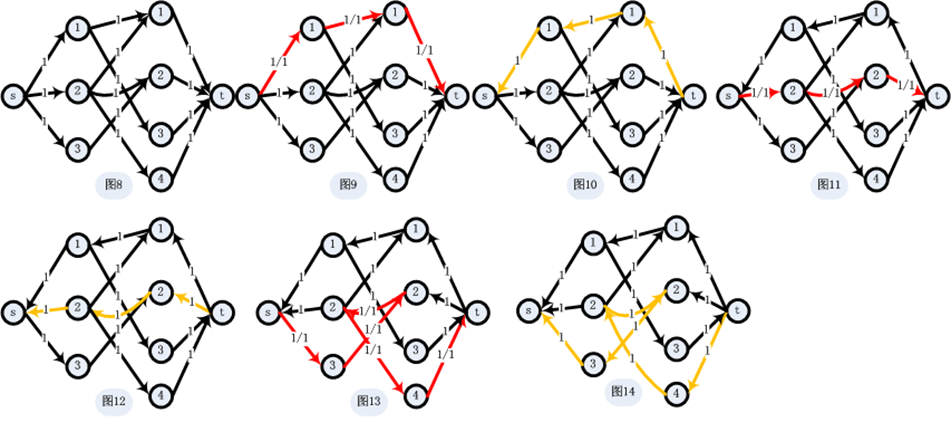
我們知道在利用最大流演算法解決最大匹配問題時,首先需要構建一個超級源點s和超級匯點t,並且邊是有方向的和容量(為1)的(如圖8所示),而利用匈牙利演算法則不需要構造s,t,邊也沒有方向和容量。表面上看匈牙利演算法中的邊沒有方向和容量,其實在它對增廣路徑的約束中我們可以看到邊的方向和容量的“影子”,如下紅色標註的約束。
匈牙利演算法對增廣路徑的約束 參見[1] :
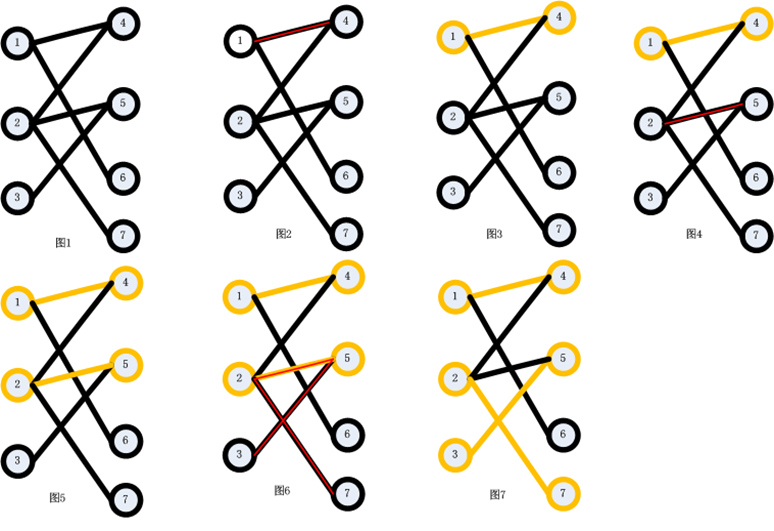
(1)有奇數條邊。 (2)起點在二分圖的左半邊,終點在右半邊。 (3)路徑上的點一定是一個在左半邊,一個在右半邊,交替出現。(其實二分圖的性質就決定了這一點,因為二分圖同一邊的點之間沒有邊相連,不要忘記哦。) (4)整條路徑上沒有重複的點。 (5)起點和終點都是目前還沒有配對的點,而其它所有點都是已經配好對的。(如圖5,圖6所示,[2,5]是已經配好對的點;而起點3和終點7目前還沒有與其它點配對。) (6)路徑上的所有第奇數條邊都不在原匹配中,所有第偶數條邊都出現在原匹配中。(如圖5,圖6所示,原有的匹配[2,5]在在圖6給出的增廣路徑(紅線所示)中是第2條邊。而增廣路徑的第1、3條邊都沒有出現在圖5給出的匹配中。) (7)最後,也是最重要的一條,把增廣路徑上的所有第奇數條邊加入到原匹配中去,並把增廣路徑中的所有第偶數條邊從原匹配中刪除(這個操作稱為增廣路徑的取反
為了便於理解,下面給出利用最大流演算法和匈牙利演算法解決最大二分匹配的圖示。圖1為初始二分圖,圖1->圖7為利用匈牙利演算法求解最大二分匹配的過程,圖8為利用圖1二分圖所構建的流網路,圖8->圖14為利用最大流演算法求解最大二分匹配的過程,最終求得的最大流為所有增廣路徑(如圖9,圖10,圖11所示)增加的流相加:1+1+1=3。
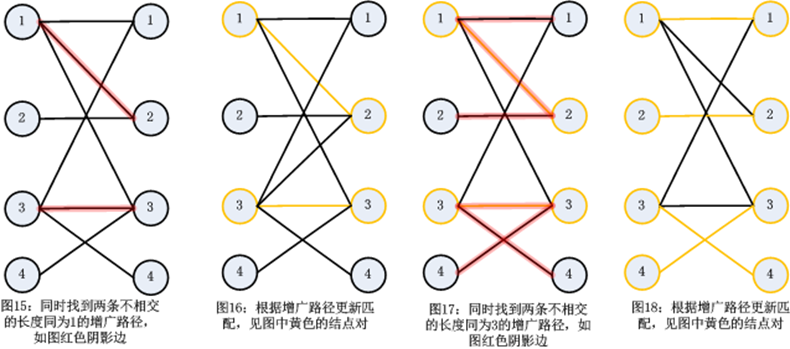
下面介紹一下Hopcroft-Karp演算法,這個演算法的時間複雜度為O(n^(1/2)*m)。該演算法是對匈牙利演算法的優化,如圖1-圖7,利用匈牙利演算法一次只能找到一條增廣路徑,Hopcroft-Karp就提出一次找到多條不相交的增廣路徑(不相交就是沒有公共點和公共邊的增廣路徑),然後根據這些增廣路徑新增多個匹配。說白了,就是批量處理!為了容易理解,我構造了一個圖例,見圖15-圖18。
回到原題中來,code1、code2分別為dfs和bfs實現的匈牙利演算法;code3為利用Hopcroft-Karp解決COURSE的程式碼。
code1:
#include<iostream>
using namespace std;
#define Maxn 500
//課程與課代表
//儲存左側的點連線的右側點
int lefts[Maxn];
//儲存右側的點 連線的左側點
int rights[Maxn];
int flag_rights[Maxn];
int G[Maxn][Maxn];
//nc代表課程數目 ns代表學生數目
int nc,ns;
int findpath(int left_u)
{
for(int v=1;v<=ns;v++)
{
if(G[left_u][v]&&!flag_rights[v])
{
flag_rights[v]=1;
if((rights[v]==-1||findpath(rights[v])))
{
lefts[left_u]=v;
rights[v]=left_u;
return 1;
}
}
}
return 0;
}
//最大匹配
int MaxMatch()
{
// printf("MaxMatch開始執行\n");
int cnt=0;
memset(lefts,-1,sizeof(lefts));
memset(rights,-1,sizeof(rights));
for(int u=1;u<=nc;u++)
{
memset(flag_rights,0,sizeof(flag_rights));
if(findpath(u))
{
cnt++;
}
}
return cnt;
}
int main()
{
int num;
scanf("%d",&num);
while(num--)
{
//首先輸入資料
memset(G,0,sizeof(G));
scanf("%d%d",&nc,&ns);
for(int u=1;u<=nc;u++)
{
int c_stu;
scanf("%d",&c_stu);
for(int j=0;j<c_stu;j++)
{
int v;
scanf("%d",&v);
G[u][v]=1;
}
}
if(ns>=nc&&MaxMatch()==nc)
{
printf("YES\n");
}
else
{
printf("NO\n");
}
}
return 0;
}
code2:
#include<iostream>
#include<queue>
#define Maxn 500
using namespace std;
//利用匈牙利演算法解決二分圖匹配問題
int nc,ns;//nc代表課程數 ns代表學生數
int lefts[Maxn];//儲存課程所對應的學生
int rights[Maxn];//儲存學生所對應的課程
int G[Maxn][Maxn];
int pre_left[Maxn];//記錄課程前面的課程 (增廣路徑)
int mark_right[Maxn];//記錄當前學生是否已經遍歷(增廣路徑)
//利用廣度優先搜尋 得到最大匹配數
int max_match()
{
//lefts 陣列初始化為0
memset(lefts,-1,sizeof(lefts));
memset(rights,-1,sizeof(rights));
int maxf=0;
for(int i=1;i<=nc;i++)
{
queue<int>q;
q.push(i);
int ok=0;
memset(mark_right,0,sizeof(mark_right));
memset(pre_left,0,sizeof(pre_left));
while(!q.empty())
{
int u=q.front();
q.pop();
for(int v=1;v<=ns;v++)
{
if(G[u][v]&&!mark_right[v])//如果課程與學生對應 並且當前學生沒有被遍歷
{
mark_right[v]=1;
if(rights[v]==-1)
{
ok=1;
//更新匹配關係
int sl=u,sr=v;
while(sl!=0)
{
int st=lefts[sl];
lefts[sl]=sr;rights[sr]=sl;
sl=pre_left[sl];sr=st;
}
break;
}
else
{
pre_left[rights[v]]=u;//記錄課程的前驅
q.push(rights[v]);
}
}
}
if(ok)
break;
}
if(ok) maxf++;
}
/*
for(int i=1;i<4;i++)
cout<<lefts[i]<<" "<<rights[i]<<endl;
*/
return maxf;
}
int main()
{
int num;
scanf("%d",&num);
while(num--)
{
memset(G,0,sizeof(G));
scanf("%d%d",&nc,&ns);
for(int i=1;i<=nc;i++)
{
int snum;
scanf("%d",&snum);
int u;
for(int j=1;j<=snum;j++)
{
scanf("%d",&u);
G[i][u]=1;
}
}
if(max_match()==nc)
{
printf("YES\n");
}
else
{
printf("NO\n");
}
/*
cout<<"最大匹配數是:"<<max_match()<<endl;
cout<<"對應的匹配關係是:"<<endl;
for(int i=1;i<=nc;i++)
{
cout<<i<<" "<<lefts[i]<<endl;
}
cout<<"!!!!!!!!!!!!!!"<<endl;
for(int i=1;i<=ns;i++)
{
cout<<rights[i]<<" "<<i<<endl;
}*/
}
return 0;
} code3:
#include<iostream>
#include<queue>
using namespace std;
const int MAXN=500;// 最大點數
const int INF=1<<28;// 距離初始值
int bmap[MAXN][MAXN];//二分圖
int cx[MAXN];//cx[i]表示左集合i頂點所匹配的右集合的頂點序號
int cy[MAXN]; //cy[i]表示右集合i頂點所匹配的左集合的頂點序號
int nx,ny;
int dx[MAXN];
int dy[MAXN];
int dis;
bool bmask[MAXN];
//尋找 增廣路徑集
bool searchpath()
{
queue<int>Q;
dis=INF;
memset(dx,-1,sizeof(dx));
memset(dy,-1,sizeof(dy));
for(int i=1;i<=nx;i++)
{
//cx[i]表示左集合i頂點所匹配的右集合的頂點序號
if(cx[i]==-1)
{
//將未遍歷的節點 入隊 並初始化次節點距離為0
Q.push(i);
dx[i]=0;
}
}
//廣度搜索增廣路徑
while(!Q.empty())
{
int u=Q.front();
Q.pop();
if(dx[u]>dis) break;
//取右側節點
for(int v=1;v<=ny;v++)
{
//右側節點的增廣路徑的距離
if(bmap[u][v]&&dy[v]==-1)
{
dy[v]=dx[u]+1; //v對應的距離 為u對應距離加1
if(cy[v]==-1) dis=dy[v];
else
{
dx[cy[v]]=dy[v]+1;
Q.push(cy[v]);
}
}
}
}
return dis!=INF;
}
//尋找路徑 深度搜索
int findpath(int u)
{
for(int v=1;v<=ny;v++)
{
//如果該點沒有被遍歷過 並且距離為上一節點+1
if(!bmask[v]&&bmap[u][v]&&dy[v]==dx[u]+1)
{
//對該點染色
bmask[v]=1;
if(cy[v]!=-1&&dy[v]==dis)
{
continue;
}
if(cy[v]==-1||findpath(cy[v]))
{
cy[v]=u;cx[u]=v;
return 1;
}
}
}
return 0;
}
//得到最大匹配的數目
int MaxMatch()
{
int res=0;
memset(cx,-1,sizeof(cx));
memset(cy,-1,sizeof(cy));
while(searchpath())
{
memset(bmask,0,sizeof(bmask));
for(int i=1;i<=nx;i++)
{
if(cx[i]==-1)
{
res+=findpath(i);
}
}
}
return res;
}
int main()
{
int num;
scanf("%d",&num);
while(num--)
{
memset(bmap,0,sizeof(bmap));
scanf("%d%d",&nx,&ny);
for(int i=1;i<=nx;i++)
{
int snum;
scanf("%d",&snum);
int u;
for(int j=1;j<=snum;j++)
{
scanf("%d",&u);
bmap[i][u]=1;
// bmap[u][i]=1;
}
}
// cout<<MaxMatch()<<endl;
if(MaxMatch()==nx)
{
printf("YES\n");
}
else
{
printf("NO\n");
}
}
//system("pause");
return 0;
}
/*