我們都知道線性迴歸例程非常簡單易懂。如果它明確指出自變數的值增加1點，則因變數增加b個單位。

但是，在預測離散變數時 - 例如，客戶是否會與服務提供商保持聯絡，或者是否會下雨 - 邏輯迴歸將會發揮作用。沒有很多不同的值，結果只能是1或0。

在本文中，我們將學習如何在Excel中構建一個簡單的客戶流失模型，我們將使用Solver通過減少交叉熵誤差來優化此模型。

在我們深入瞭解邏輯迴歸的細節之前，讓我們理解為什麼當我們必須基於線性迴歸的以下限制來預測離散結果時，線性迴歸不起作用：

• 線性迴歸假設每個變數之間存線上性關係。但是，如果與競爭對手相比，客戶為特定服務支付的費用較低，則客戶離開服務提供商的機會將呈指數級變化。

• 線性迴歸假設隨著自變數的增加，概率成比例地增加。

解決方案：Sigmoid曲線救援

如上所述，線性迴歸的主要問題是它假設變數之間存線上性關係，這在實踐中非常罕見。

為了解決這個（以及其他一些）限制問題，我們將探索S形曲線。在外行人的語言中，我們可以說sigmoid函式（曲線）有助於返回概率值，然後可以將概率值對映到兩個或更多個離散類。然而，一般來說，線性迴歸並不能告訴我們在某個範圍之後事件發生的概率。

基於以上解釋，我們可以說S形曲線可以比線性迴歸更好地解釋離散現象。

為了簡單起見，我將繼續討論本文的核心主題，即如何使用邏輯迴歸來留住客戶。為此，我們將努力瞭解邏輯迴歸並瞭解如何實施。

眾所周知，線性迴歸假設依賴變數和自變數之間存線上性關係。它表示為Y = x + b * X. Logistic迴歸通過應用S形曲線遠離線性關係的概念。

上述符號清楚地表明邏輯迴歸如何使用自變數，這與線性迴歸相同。但是，同時，它還通過sigmoid啟用將這些變數傳遞給0到1之間的輸出。

現在，要看一下邏輯迴歸中輸出如何變化，讓我們藉助一個例子來看一下邏輯迴歸方程的內幕：

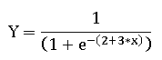
• 如果X = 0，則Y = 1 /（1 + exp（ - （2）））= 0.88

• 如果X增加2個單位（即X = 2），則Y的值為Y = 1 /（1 + exp（ - （2 + 3 * 2）））= 1 /（1 + exp（ - （（ 5）））= 0.993

很明顯Y的值從0.88變為0.99，因為X從0變為2.同樣，如果X為-2，則Y將為0.017。因此，X中單位變化對Y的影響取決於等式。當X = 0時，值0.88可以解釋為概率。例如，平均在88％的情況下，當X = 0時，Y的值為1。

物流回歸在行動中

為了看到上面的等式和例程，我們將在Excel中執行構建邏輯迴歸方程。挑戰在於能夠根據下表中列出的一些變數來預測客戶是否會與服務提供商保持聯絡。

要遵循的步驟

1. 將自變數的權重初始化為隨機值（假設各自為1）。

2. 一旦權重和偏差被初始化，我們將通過對獨立變數的多元線性迴歸應用S形啟用來估計輸出值（客戶離開的概率= 1或停留= -0）。

下表包含有關sigmoid曲線的（a + b * X）部分和最終sigmoid啟用值的資訊：

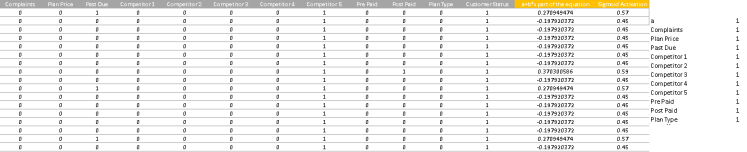
獲得上表中的數值的公式如下表所示：

前面的sigmoid啟用col中的if條件。只是因為Excel在計算任何值> exp 500時有限制 - 因此裁剪。

誤差估計

線上性迴歸中，我們考慮實際值和預測值之間的最小二乘（平方差）來估計總誤差。在邏輯迴歸中，我們將使用稱為交叉熵的不同誤差度量。

交叉熵是兩種不同分佈之間差異的度量 - 實際和預測分佈。

在因變數（Customer Churn）為1的情況下，讓我們看一下兩個成本函式（最小二乘法和熵成本）：

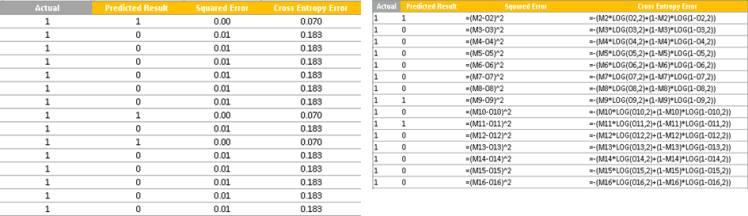
上表清楚地表明，與平方誤差相比，交叉熵方法對高預測誤差進行了大量懲罰：較低的誤差值在平方誤差和交叉熵誤差方面具有相似的損失，但是在存在高差異的情況下，交叉熵懲罰巨資。因此，在預測離散變數時，堅持使用交叉熵誤差作為誤差度量是一個好主意。

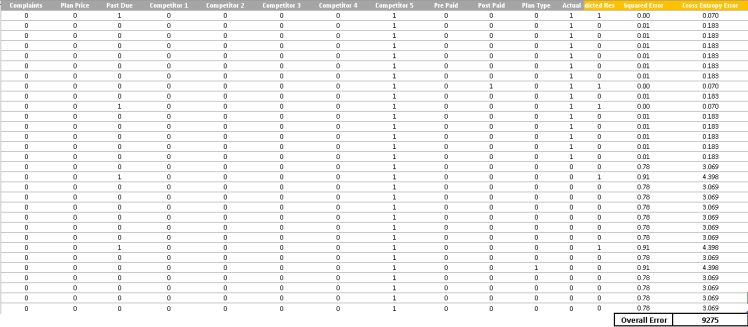
現在我們已經設定了問題，讓我們改變引數，以減少整體錯誤。此步驟可以通過梯度下降來執行，這可以通過使用excel中的Solver功能來完成。

如何使用Solver執行邏輯迴歸？

注意：為了提高模型效能並減少錯誤，最好只引入具有統計意義的變數。對於此活動，可以遵循超出本文範圍的不同方法。