導語

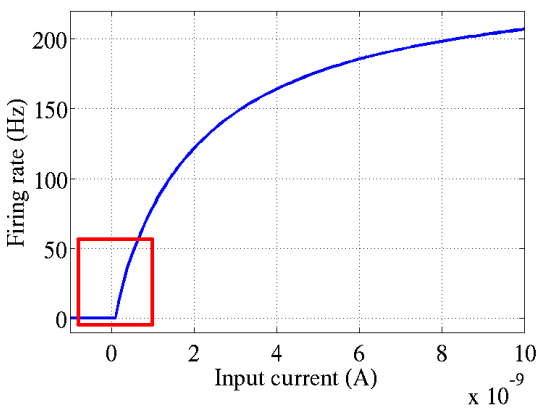
在深度神經網路中，通常使用一種叫修正線性單元(Rectified linear unit，ReLU）作為神經元的啟用函式。ReLU起源於神經科學的研究：2001年，Dayan、Abott從生物學角度模擬出了腦神經元接受訊號更精確的啟用模型，如下圖：

  其中橫軸是時間(ms)，縱軸是神經元的放電速率(Firing Rate)。同年，Attwell等神經科學家通過研究大腦的能量消耗過程，推測神經元的工作方式具有稀疏性和分佈性；2003年Lennie等神經科學家估測大腦同時被啟用的神經元只有1~4%，這進一步表明了神經元的工作稀疏性。而對於ReLU函式而言，類似表現是如何體現的？其相比於其他線性函式(如purlin)和非線性函式(如sigmoid、雙曲正切)又有何優勢？下面請各位看官容我慢慢道來。

簡單之美

首先，我們來看一下ReLU啟用函式的形式，如下圖：    從上圖不難看出，ReLU函式其實是分段線性函式，把所有的負值都變為0，而正值不變，這種操作被成為單側抑制。可別小看這個簡單的操作，正因為有了這單側抑制，才使得神經網路中的神經元也具有了稀疏啟用性。尤其體現在深度神經網路模型(如CNN)中，當模型增加N層之後，理論上ReLU神經元的啟用率將降低2的N次方倍。這裡或許有童鞋會問：ReLU的函式影象為什麼一定要長這樣？反過來，或者朝下延伸行不行？其實還不一定要長這樣。只要能起到單側抑制的作用，無論是鏡面翻轉還是180度翻轉，最終神經元的輸出也只是相當於加上了一個常數項係數，並不影響模型的訓練結果。之所以這樣定，或許是為了契合生物學角度，便於我們理解吧。

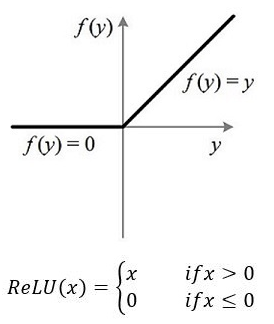
那麼問題來了：這種稀疏性有何作用？換句話說，我們為什麼需要讓神經元稀疏？不妨舉栗子來說明。當看名偵探柯南的時候，我們可以根據故事情節進行思考和推理，這時用到的是我們的大腦左半球；而當看蒙面唱將時，我們可以跟著歌手一起哼唱，這時用到的則是我們的右半球。左半球側重理性思維，而右半球側重感性思維。也就是說，當我們在進行運算或者欣賞時，都會有一部分神經元處於啟用或是抑制狀態，可以說是各司其職。再比如，生病了去醫院看病，檢查報告裡面上百項指標，但跟病情相關的通常只有那麼幾個。與之類似，當訓練一個深度分類模型的時候，和目標相關的特徵往往也就那麼幾個，因此通過ReLU實現稀疏後的模型能夠更好地挖掘相關特徵，擬合訓練資料。

此外，相比於其它啟用函式來說，ReLU有以下優勢：對於線性函式而言，ReLU的表達能力更強，尤其體現在深度網路中；而對於非線性函式而言，ReLU由於非負區間的梯度為常數，因此不存在梯度消失問題(Vanishing Gradient Problem)，使得模型的收斂速度維持在一個穩定狀態。這裡稍微描述一下什麼是梯度消失問題：當梯度小於1時，預測值與真實值之間的誤差每傳播一層會衰減一次，如果在深層模型中使用sigmoid作為啟用函式，這種現象尤為明顯，將導致模型收斂停滯不前。