資料結構圖知識點小結
圖的遍歷:
深度優先:

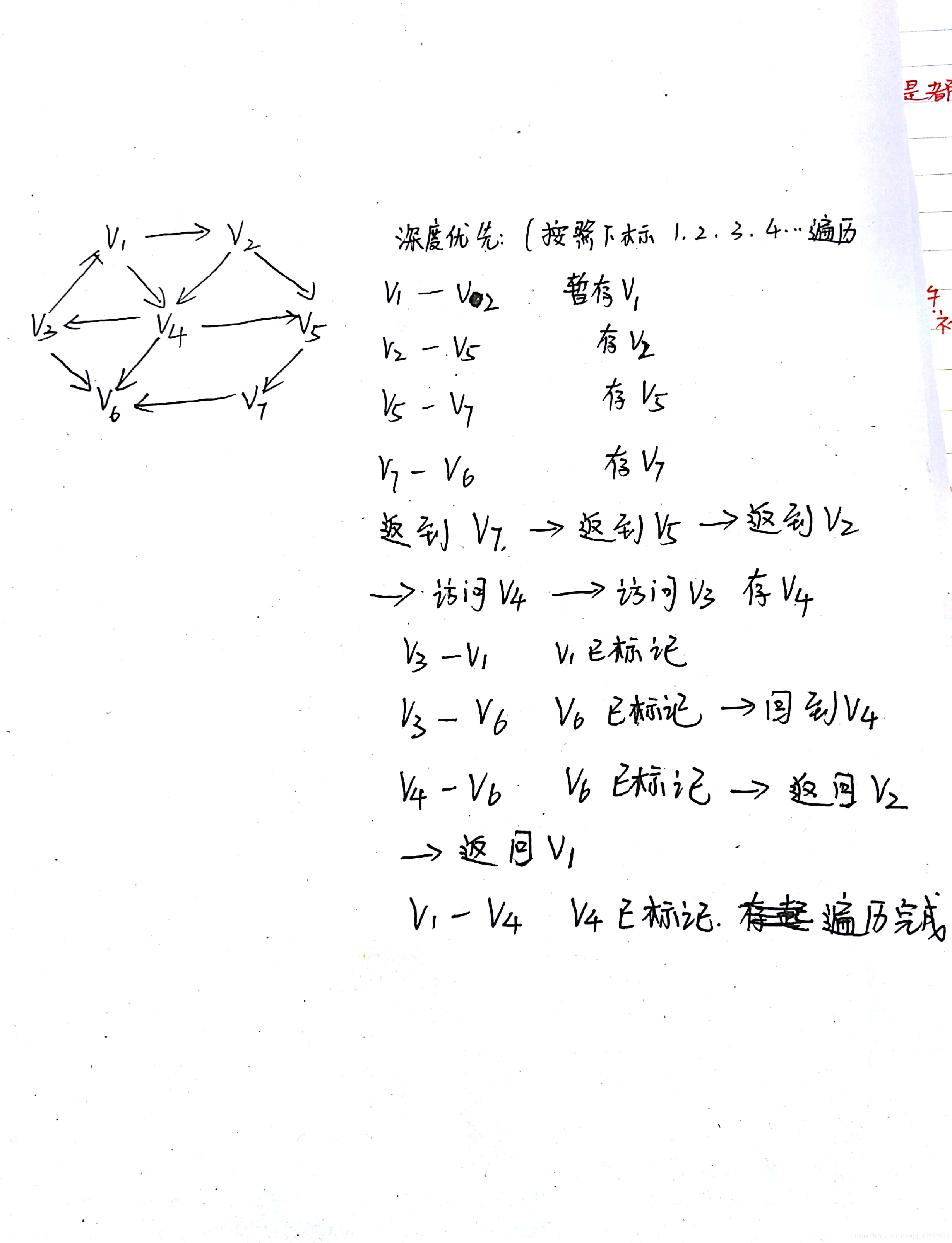
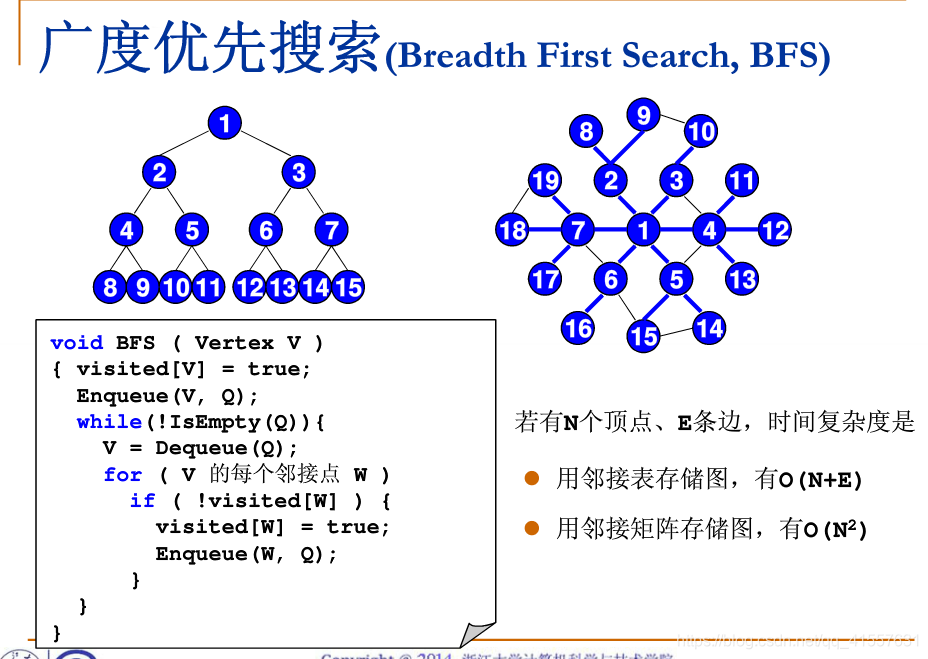
廣度優先:
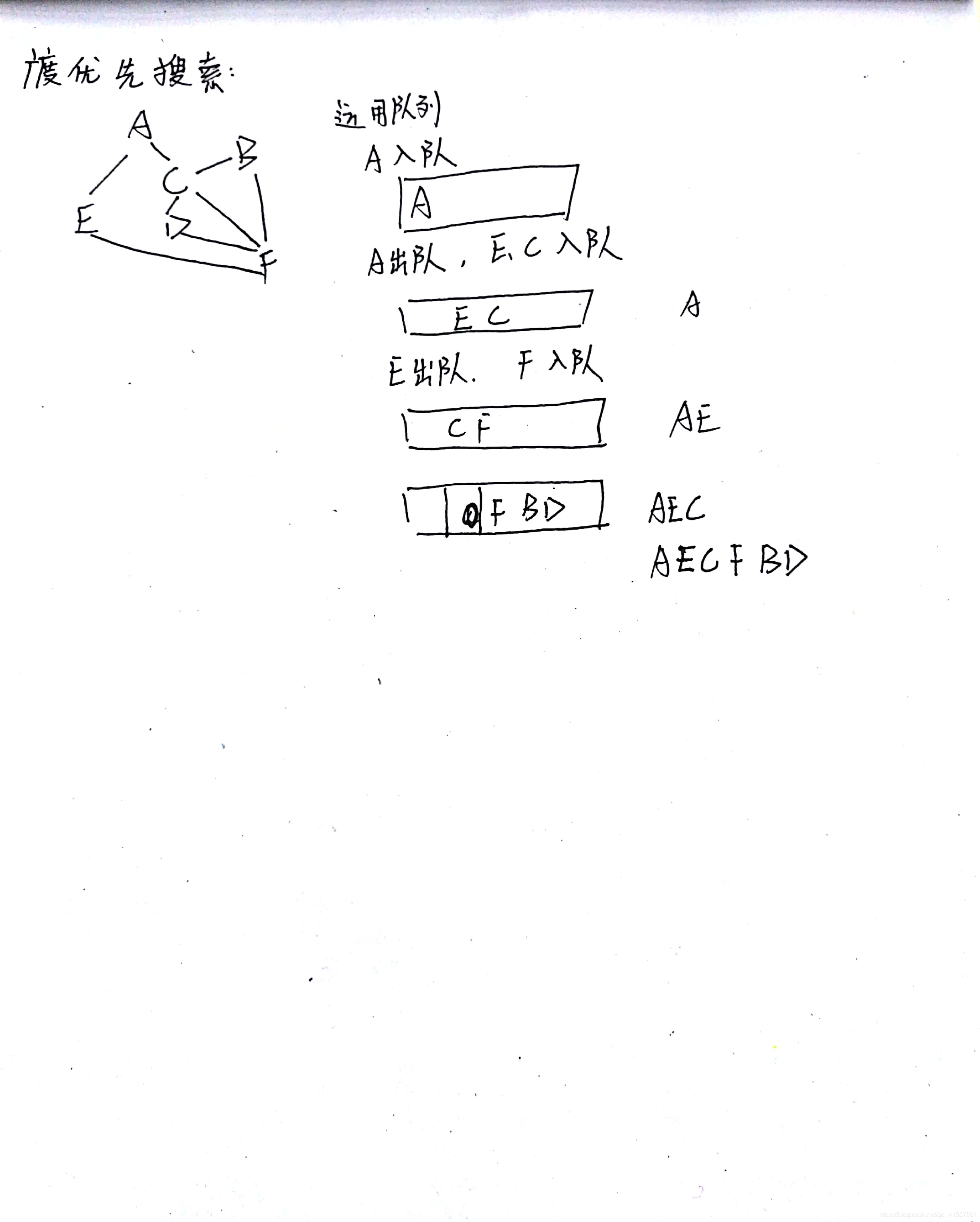
最小生成樹:
必須滿足條件:演算法完成後不能存在迴路;V個頂點就只有V-1條邊;必須包含所有頂點
PS:若生成樹成功,一定是連通圖。若生成樹失敗,原圖不連通
定義所有頂點為S,每次收錄進去的組成集合V,剩下的是集合S-V
一、KRUSKAL演算法:
思路:每次都收錄權重最小的邊進入集合V(這條邊不能構成迴路)直到收錄了所有頂點
PS:這種思路的出發點是邊,可以用小頂堆來儲存邊的權重。
 二、PRIM演算法:
二、PRIM演算法:
從第一個點開始,收錄到集合V中,看與集合V相連的點,權重最小的收錄進去(不能構成迴路),注意每次收錄的點是與集合V相連的點,這個點可以依賴於集合V中的任何一個結點。
兩種演算法如下所示:
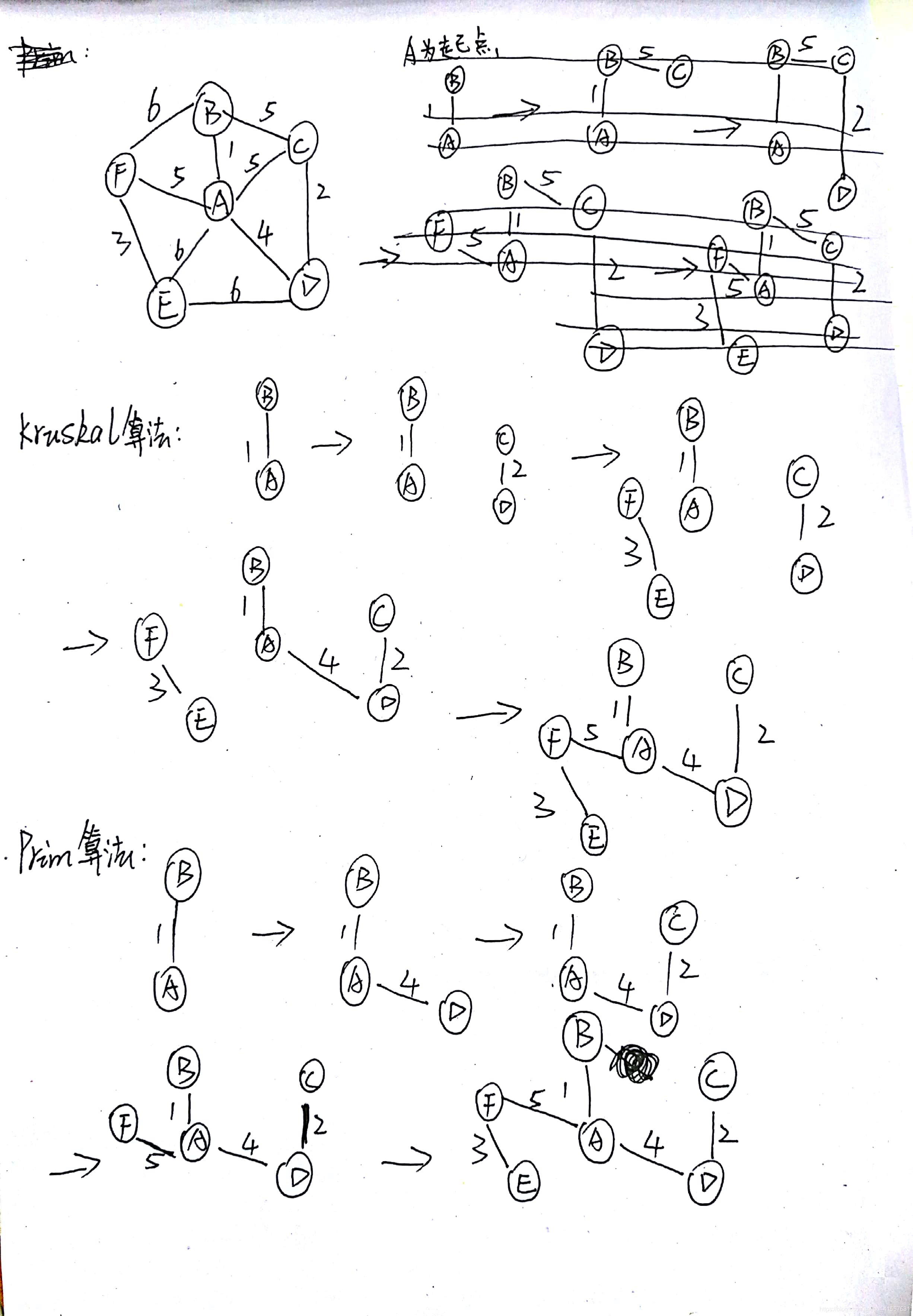
拓撲排序:
定義:如果從V 到W有一條有向路徑,V一定要排在W前面。
能夠進行拓撲排序的一定是有向無環圖。

最短路徑
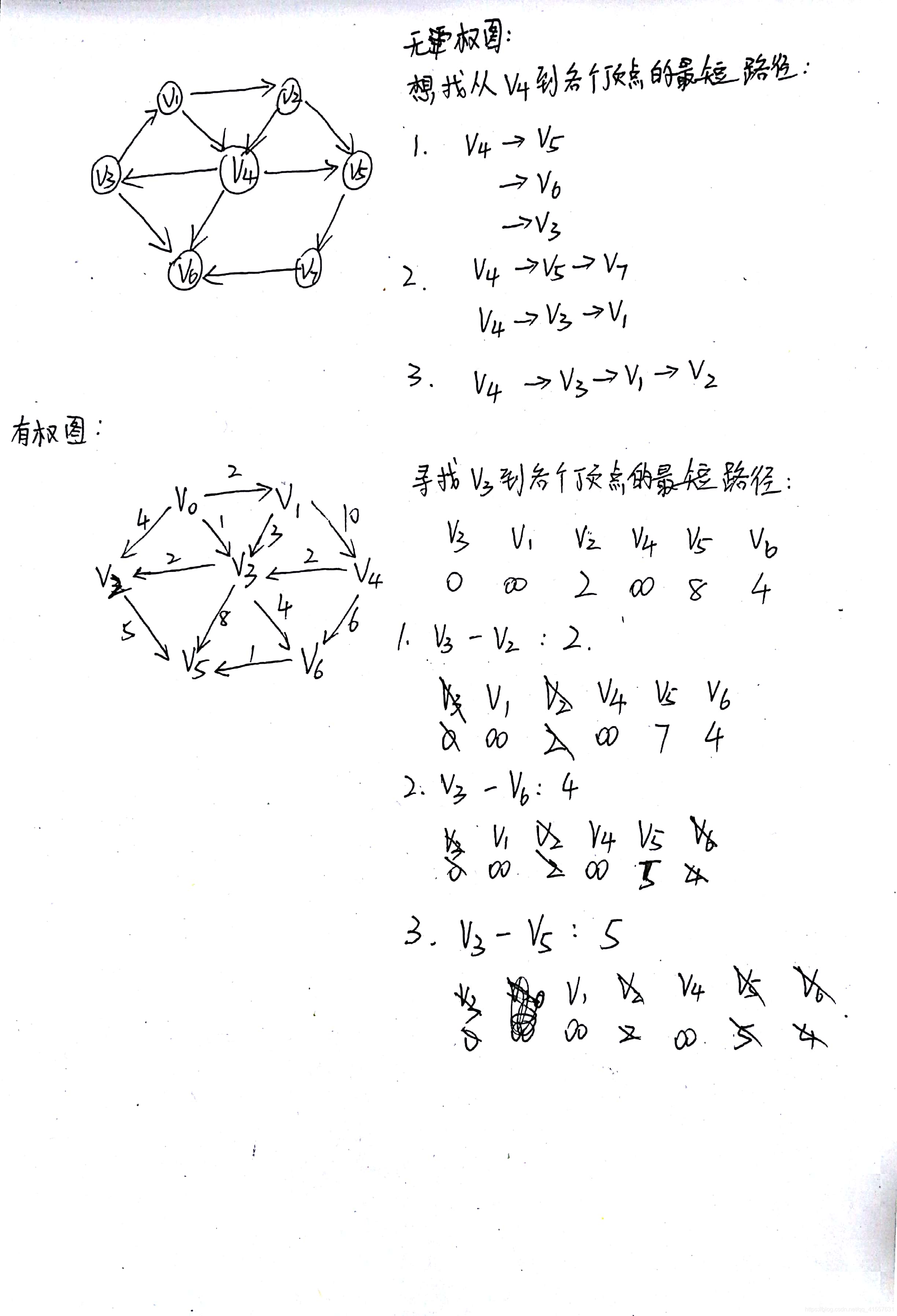
單源無權圖的最短路徑:
按照遞增的順序依次排列,直到求出從源點到目標點的最短路徑;
多源有權圖最短路徑:
Dijkstra演算法:按照遞增的順序依次排列,直到求出源點到目標點的最短路徑;
示例如下:
相關推薦
資料結構圖知識點小結
圖的遍歷: 深度優先: 廣度優先: 最小生成樹: 必須滿足條件:演算法完成後不能存在迴路;V個頂點就只有V-1條邊;必須包含所有頂點 PS:若生成樹成功,一定是連通圖。若生成樹失敗,原圖不連通 定義所有頂點為S,每次收錄進去的組成集合V,剩下的是集合S-V 一、KRUSK
資料結構-圖-知識點總結
一、基本術語 圖(graph):圖是由頂點的有窮非空集合和頂點之間邊的集合組成,通常表示為:G(V,E),其中,G表示一個圖,V是圖G中的頂點的集合,E是圖G中邊的集合。 頂點(Vertex):圖中的資料元素。線性表中我們把資料元素叫元素,樹中將資料元素叫結點。 邊:頂點之間的邏輯關係用邊來表示,邊集可
資料結構---圖---知識點總結
轉自:https://blog.csdn.net/Ontheroad_/article/details/72739380圖的儲存結構1.鄰接矩陣:兩個陣列,一個數組儲存“頂點集”,一個數組儲存“邊集”。無向圖中:有向圖中:2.鄰接表:陣列與連結串列相結合的儲存方法。對於帶權值
資料結構 圖的深度優先遍歷 C
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!
大話資料結構--圖的最小生成樹-java實現
普利姆(Prim)演算法 最小生成樹 * A * / | \ * B- -F- -E * \ / \ / * C -- D * A B C D E F * 0 1 2 3 4 5 * * A-B 6 A-
大話資料結構--圖的遍歷-java實現
圖的遍歷分為深度優先遍歷和廣度優先遍歷 總結下圖的遍歷: 深度優先遍歷 就像一棵樹的前序遍歷 A B C D E F G H A 1 1 B 1 1 1 C 1 1 1
資料結構——圖(2)——圖的儲存和表示方式.md
圖的儲存方式 在實踐中,圖最常見的策略是: 將每個節點的連線儲存在鄰接列表中。 將整個圖形的連線儲存在鄰接矩陣中。 用鄰接連結串列來表示圖之間的關係 在圖中表示連線的最簡單方法是在每個節點的資料結構中儲存與其連線的節點的列表。該結構稱為鄰接列表。 例如
資料結構——圖(3)——深度優先搜尋演算法(DFS)思想
圖的遍歷 圖由頂點及其邊組成,圖的遍歷主要分為兩種: 遍歷所有頂點 遍歷所有邊 我們只討論第一種情況,即不重複的列出所有的頂點,主要有兩種策略:深度優先搜尋(DFS),廣度優先搜尋(BFS) 為了使深度和廣度優先搜尋的實現演算法的機制更容易理解,假設提
資料結構——圖(1)——圖的簡單介紹
圖的簡介 我們先回顧一下之前介紹的樹的概念,在樹的定義中,每個節點只能有一個父類,並且樹中不能出現有環形。但是你可曾想過,當一棵樹沒有任何規則的時候,會發生什麼嗎? 現在,我們給圖(graph)下一個定義: 圖,是一種用節點和邊來表示相互關係的數學模型。(A graph is a
資料結構——圖(7)——最短路徑與Dijkstra's Algorithm
帶權圖 在圖中,給每一條路徑帶上一定的權重,這樣的圖我們稱為帶權圖。如下圖所示: 我們現在來回顧一下BFS跟DFS的基本思想: 深度優先搜尋:繼續沿著路徑搜尋,直到我們需要回溯,但這種方式不保證最短路徑。 廣度優先搜尋:檢視包含距離1的鄰居,然後是距離2的鄰
資料結構——圖(6)——深入分析BFS演算法
DFS的不足和BFS演算法 雖然我們知道根據DFS演算法我們可以找到所有的,由起始節點到目標節點的所有路徑,但並不代表那條路是最短的或者是最佳的。就像我們上篇文章所說的一樣,對於同一幅圖,非遞迴演算法找到的路徑就明顯比遞迴演算法找的要短。 回顧我們之前提到的BFS的基本思想:從起始頂
資料結構——圖(5)——深入分析DFS演算法
對DFS的過程分析 在前面的文章中我們提到了這樣的一幅圖: 我們知道,在DFS中,我們採用的是遞迴的方式進行實現的,並且給每一個遍歷過的點都做上了標記,目的是為了防止程式進入死迴圈。(為什麼樹可以不需要呢?因為樹沒有環) 利用之前專欄提到的遞迴模式,我們可以寫出下面的虛擬碼:
資料結構——圖(4)——廣度優先搜尋(BFS)演算法思想
廣度優先搜尋 儘管深度優先搜尋具有許多重要用途,但該策略也具有不適合某些應用程式的缺點。 深度優先方法的最大問題在於它從其中一個鄰居出發,在它返回該節點或者是訪問其他鄰居之前,它必須訪問完從出發節點開始的整個路徑。 如果我們嘗試在一個大的圖中發現兩個節點之間的最短路徑,則使用深度優先
資料結構——圖(9)——拓撲排序與DFS
DAG圖與AOV網 一個無環的有向圖稱為有向無環圖(DAG)。圖的頂點可以表示要執行的任務,並且邊可以表示一個任務必須在另一個之前執行的約束; 在這個應用程式中,拓撲排序只是任務的有效序列。 當且僅當圖形沒有有向迴圈時,即如果它是有向無環圖(DAG),則可以進行拓撲排序。 任何DAG
資料結構——圖(8)——最小生成樹(MST)
問題的提出 如下圖,假設這裡有一系列的房屋,問如何鋪設電線,可以使得連線所有房屋的電線的總成本最低?這是20世紀20年代早期研究最小生長樹的最初動機。 (捷克數學家OtakarBorůvka完成的工作)。 最短路徑樹與最小生成樹(MST) 上次,我們看到了Dijkstra演
資料結構-圖-C語言-PTA-Complete Binary Search Tree
Data Structures and Algorithms (English) 7-7 Complete Binary Search Tree #include <stdio.h> #include <stdlib.h> #include <math.
資料結構-圖-C語言-鄰接矩陣-圖的遍歷
資料結構-圖-C語言-鄰接矩陣-圖的遍歷 bool visited[999]; void visit(Vertex V) { printf("正在訪問頂點%d\n", V); } bool isEdge(MGraph graph, Vertex v, Vertex w) { re
資料結構-圖-C語言-PTA-Saving James Bond - Easy Version
Data Structures and Algorithms (English) 7-10 Saving James Bond - Easy Version 以下為自己寫的版本,難過的是測試點2無法通過 #include <stdio.h> #include <
java中的資料結構——圖
圖是一種以網路形式相互連線的節點,圖是一種與樹有些相似的資料結構,圖通常有一個固定的形狀, 這是由物理或抽象的問題所決定的。圖包含由邊連線的頂點。 型別,無向圖,有向圖(邊有方向,通常用箭頭表示) 圖可以用兩種形式表示,鄰接矩陣,鄰接表,鄰接矩陣或鄰接表提供了關於當前頂點的位置資訊,當前 頂
Python資料結構——圖(graph)
圖由頂點和邊組成。如果圖中頂點是有序的,則稱之為有向圖。 由頂點組成的序列,稱為路徑。 除了可以對圖進行遍歷外,還可以搜尋圖中任意兩個頂點之間的最短路徑。 在python中,可利用字典 {鍵:值} 來建立圖。 圖中的每個頂點,都是字典中的鍵,該鍵對應的值為“該頂點所指向的圖
